ill М I Ml И I I I И I I I 1 I И I I i И

39 26

1111 i 11111 м 111 И I m

13 8 4

РИСУНОК 6.11. 4- И 13-УПОРЯДОЧЕННЫЙ ФАЙЛ.

Нижний ряд изображает массив, при этом заштрихованные квадратики обозначают элементы, которые должны быть меньше или равны крайнему правому элементу массива, если этот массив 4- и 13-упорядоченный. 4 верхних ряда отражают, как появился нижний ряд. Если элемент справа находится в массиве в позиции i, то 4-упорядочение означает, что элементы массива в позициях i-4, i-8, i-12, ... меньше или равны ему (верхний ряд); 13-упорядочение означает, что элемент i-13, а вместе с ним, в силу 4-упорядочения, и элементы i-17, i-2I, i-25, ... меньше или равны ему (второй ряд сверху); по той же причине элемент в позиции i-26, а вместе с ним, в силу 4-упорядочения, и элементы i-30, i-34, i-38, ... меньше или равны ему (третий ряд сверху), и т.д. Оставшиеся незаштрихованными квадратики суть те, которые могут быть больше, чем элемент слева; в рассматриваемом примере таких элементов самое большее 18 (дальше всех находится элемент в позиции i-36). Таким образом, потребуется выполнить самое большее 18N сравнений при сортировке вставками 13- и 4-упорядоченного файла, состоящего из N элементов.

Последовательности шагов, которые рассматривались до сих пор, эффективны в силу того, что следующие один за другим элементы последовательности взаимно просты. Другое семейство последовательностей шагов эффективно именно благодаря тому, что такие элементы не являются взаимно простыми.

В частности, из доказательства леммы 6.8 следует, что в процессе завершающей сортировки вставками 2- и J-упорядоченного файла каждый элемент перемещается самое большее на одну позицию. Это значит, что такой файл может быть отсортирован за один проход пузырьковой сортировки (отпадает необходимость в дополнительном цикле). Теперь, если файл --упорядочен и 5-упорядочен, то из этого следует, что каждый элемент перемещается максимум на одну позицию, если выполнить его 2-упорядочение (поскольку каждый подфайл 2- и J-упорядочен); и если файл 6-упоря-дочен и 9-упорядочен, то каждый элемент перемещается самое большее на одну позицию при его J-сортировке. Продолжая рассуждения в этом направлении, мы приходим к идее, которую Пратт опубликовал в 1971 г. (см. раздел ссылок).

Метода Пратта основан на использовании треугольника шагов, причем каждое входящее в этот треугольник число в два раза больше числа, стоящего сверху справа, и в три раза больше числа, стоящего в треугольнике сверху слева.

2 3 4 6 9 8 12 18 27 16 24 36 54 81 32 48 72 108 162 243 64 96 144 216 324 486 729

Если мы используем эти числа снизу вверх и справа налево как последовательность шагов в рамках сортировки методом Шелла, то каждому шагу х в нижнем ряду предшествуют значения 2х и Зх, так что каждый подфайл оказывается 2-упорядочен и J-упорядочен и ни один элемент не передвигается больше, чем на одну позицию в процессе всей сортировки!

Таблица 6.2. Эмпирическое исследование последовательностей

шагов сортировки методом Шелла.

Сортировка методом Шелла выполняется в несколько раз быстрее по сравнению с другими элементарными методами сортировки даже в тех случаях, когда шаги являются степенями 2, в то же время некоторые специальные виды последовательностей шагов позволяют увеличить ее быстродействие в 5 и более раз. Три лучших последовательности, приведенные в данной таблице, существенно различаются по положенным в их основу принципам. Сортировка методом Шелла вполне пригодна для практических приложений даже в случае файлов больших размеров; по эффективности она намного превосходит методы выбора и вставок, равно как и пузырьковую сортировку (см. таблицу 6.1).

0 1 2 4 8 16 32 64 128 256 512 1024 2048...

К 1 4 13 40 121 364 1093 3280 9841 ... (лемма 6.9)

G 1 2 4 10 23 52 113 249 548 1207 2655 5843 ... (упражнение 6.40)

S 1 8 23 77 281 1073 4193 16577 ... (лемма 6.10)

Р 1 7 8 49 56 64 343 392 448 512 2401 2744 ... (упражнение 6.44)

1 1 5 19 41 109 209 505 929 2161 3905 ... (упражнение 6.45)

Лемма 6.11. Сортировка методом Шелла выполняет менее О {N { logN)) операций сравнения для последовательности щагов 1 2 3 4 6 9 8 12 18 27 16 24 36 54 81...

Число шагов из треугольника, которое меньше Л по величине, и подавно будет меньше (log2A).

Последовательности шагов, предложенные Праттом, на практике проявляют тенденцию работать хуже, чем другие, поскольку, их слишком много. Мы можем воспользоваться тем же принципом построения последовательностей шагов на базе любых двух взаимно простых чисел Ник. Такие последовательности шагов показывают хорошие результаты, поскольку границы в худших случаях, соответствующие лемме 6.11, дают завышенную оценку стоимости сортировки файлов с произвольной организацией.

Проблема построения хорошей последовательности шагов для сортировки методом Шелла представляет собой прекрасный пример сложного поведения простых ал-

горитмов. Разумеется, мы, не имеем возможности анализа всех алгоритмов, которые будут встречаться далее, на таком же уровне детализации (этому препятствует не только ограниченное пространство данной книги, но, как и в случае сортировки методом Шелла, может произойти так, что потребуется математический анализ, выходящий за рамки материала книги, а, возможно, и специальные исследования). Тем не менее, многие алгоритмы, рассматриваемые в данной книге, являются результатом широких аналитических и эмпирических исследований, выполненных исследователями за несколько последних десятилетий, посему можно воспользоваться плодами их трудов. Эти исследования показывают, что задача повышения эффективности сортировки во многих случаях представляет собой интересную научную проблему и часто приносит неплохие практические результаты, даже в случаях простых алгоритмов. В табл. 6.2 приведены эмпирические данные, которые показывают, что некоторые подходы к построению последовательностей шагов хорошо работают на практике; относительно короткая последовательность 1 8 23 77 281 1073 4193 16577 ... - одна из самых простых, какие используются в программных реализациях сортировки методом Шелла.

Из рис. 6.13. следует, что сортировка методом Шелла обеспечивает хорошие результаты на различных видах файлов и несколько хуже - в случае файлов с произвольной организацией. В самом деле, построение файла, на котором сортировка методом Шелла выполняется медленно на заданной последовательности шагов, - достаточно сложная задача (см. упражнение 6.42). Как уже отмечалось ранее, существуют плохие последовательности шагов, при использовании которых в сортировке методом Шелла требуемое число операций сравнения в наихудшем случае находится в квадратичной зависимости от размера файла (см. упражнение 6.36), однако доказано, что для широкого набора таких последовательностей эта оценка намного лучше.

Сортировка методом Шелла выбирается для многих приложений, поскольку она обеспечивает приемлемое время сортировки даже для достаточно больших файлов и реализуется в виде компактной программы, которую легко заставить работать. В следующих главах мы ознакомимся с методами сортировки, которые, возможно, более ют всего лишь в два раза быстрее (а то и того меньше) при но при этом они существенно сложнее. Короче говоря, если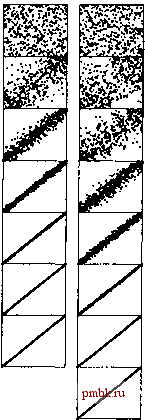

РИС. 6.12. ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ СОРТИРОВКИ МЕТОДОМ ШЕЛЛА (ДВЕ РАЗЛИЧНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ ШАГОВ)

Представленный на рисунке процесс выполнения сортировки методом Шелла можно сравнить с резиновой лентой, неподвижно закрепленной в прот ивоположных углах, когда все точки ленты устремляются в направлении диагонали. Отображены две последовательности шагов: 1214013 41 (слева) и 209 109411951 (справа). Вторая последовательность требует выполнения на один проход больше, но в то же время она выполняется быстрее, поскольку каждые ее проход более эффективен.

эффективны, но работа-небольших значениях Л, необходимо решить про-