живается на диаграмме размером Лна Л, представленной на рис. 6.3, которая подробно иллюстрирует работу алгоритма сортировки вставками. Здесь ведется подсчет элементов, лежащих под главной диагональю, причем в наихудшем случае учитываются все такие элементы. Можно ожидать, что для случайно распределенных входных данных каждый элемент пройдет в среднем половину пути назад, следовательно, необходимо учитывать только половину элементов, лежащих ниже диагонали.

Лемма 6.3. Пузырьковая сортировка производит в среднем примерно V 2 операций сравнения и N/2 операций обмена как в среднем, так и в наихудшем случаях.

На /-М проходе пузырьковой сортировки нужно выполнить N - i операций сравнения-обмена, следовательно, лемма 6.3 доказывается так же, как и случае сортировки выбором. Если алгоритм усовершенствован таким образом, что его выполнение прекращается, как только он обнаруживает, что файл уже отсортирован, то время его выполнения зависит от природы входных данных. Если файл уже отсортирован, то достаточно всего лишь одного прохода, однако /-й проход требует выполнения jV-/операций сравнения и обмена, если файл отсортирован в обратном порядке. Как отмечалось ранее, эффективность сортировки для обычного случая ненамного выше, чем для самого трудного случая, однако анализ, благодаря которому был установлен этот факт, достаточно сложный {см. раздел ссылок).

И хотя понятие частично отсортированного файла уже по своей природе содержит в себе неопределенность, сортировка вставками и пузырьковая сортировка показывают хорошие результаты при работе с файлами, не обладающими произвольной организацией, которые довольно часто встречаются на практике. Применение в такого рода приложениях универсальных методов сортировки нецелесообразно. Например, рассмотрим, как работает сортировка вставками на файле, который уже является отсортированным. Сразу же выясняется, что все элементы файла находятся на своих местах, а общие затраты времени на сортировку линейно зависят от числа элементов. Это же утверждение справедливо и в отношении пузырьковой сортировки, но для сортировки выбором эта зависимость остается квадратичной.

Определение 6.2. Инверсией называется пара ключей, которые нарушают порядок в файле.

Для подсчета количества инверсий в файле для каждого элемента потребуется просуммировать число элементов слева, которые превосходят его по величине (мы будем называть это значение числом инверсий, соответствующих выбранному элементу). Но это число есть в точности расстояние, которое должны пройти эти элементы во время сортировки вставками. В частично отсортированном файле меньше инверсий, чем в произвольно упорядоченном файле.

Существуют такие типы частично отсортированных файлов, в которых каждый элемент находится достаточно близко к своей окончательной позиции. Например, некоторые игроки в карты сортируют имеющиеся у них на руках карты, сначала располагая их по масти, тем самым помещая близко к их окончательным позициям, а затем упорядочивают карты каждой масти по старшинству. Далее мы рассмотрим некоторое число методов сортировки, которые действуют примерно таким же образом - на начальной стадии они размещают элементы вблизи окончательных позиций, в

РИСУНОК 6.6. ОПЕРАЦИИ СРАВНЕНИЯ И ОБМЕНА ЭЛЕМЕНТОВ В УСЛОВИЯХ ЭЛЕМЕНТАРНЫХ МЕТОДОВ СОРТИРОВКИ

На этой диаграмме показаны различия в том, как сортировки вставками, выбором, а также пузырьковая сортировка приводят конкретный файл в порядок. Сортируемый файл представлен в виде отрезков, которые сортируются по углу наклона. Черные отрезки соответствуют элементам, к которым в процессе сортировки производится доступ на каждом проходе; серые отрезки соответствуют элементам, которые не затрагиваются. В условиях сортировки вставками (слева) вставляемый элемент проходит примерно половину пути назад через отсортированную часть на каждом проходе. Сортировка выбором (в центре) и пузырьковая сортировка (справа) проходят на каждом проходе через всю неотсортированную часть массива с целью обнаружения там следующего наименьшего элемента; различие между этими методами заключается в том, что пузырьковая сортировка меняет местами каждую пару соседних элементов, нарушающих порядок, которые ей удается обнаружить, в то время как сортировка выбором помещает минимальный элемент в окончательную позицию. Это различие проявляется в том, что по мере выполнения пузырьковой сортировки, неотсортированная часть массива становится все более упорядоченной.

результате чего образуется частично упорядоченный файл, в котором каждый элемент расположен недалеко от той позиции, которую он в конечном итоге должен занять. Высокую эффективность при сортировке таких файлов демонстрируют сортировка вставками и пузырьковая сортировка (но не сортировка выбором).

Лемма 6.4. Методы вставок и пузырьковой сортировки выполняют линейно зависимое от Л число операций сравнения и обмена при сортировке файлов с не более чем постоянным числом инверсий, приходящихся на каждый элемент.

Как было только что отмечено, время выполнения сортировки вставками прямо пропорционально количеству инверсий в сортируемом файле. Что касается пузырьковой сортировки (здесь мы ссылаемся на программу 6.4, скорректированную таким образом, что ее выполнение прекращается, как только заверщена сортировка файла), то доказательство подобного утверждения требует дополнительных рассуждений (см. упражнение 6.29). Каждый проход пузырьковой сортировки уменьшает справа от любого элемента число меньших его элементов точно на 1 (если, естественно, это число не было равным 0), следовательно, пузырьковая сортировка использует не более чем постоянное число проходов для типов файлов, которые сейчас рассматриваются (т.е. частично упорядоченных), и поэтому количество выполняемых операций сравнения и обмена линейно зависит от N.

Другой тип частично отсортированных файлов может быть получен за счет добавления нескольких элементов к уже отсортированному файлу либо путем соответствующего изменения ключей нескольких элементов отсортированного файла. Подобные типы файлов наиболее часто встречаются в приложениях сортировки. Для таких файлов наиболее эффективным является сортировка вставками: сортировка выбором и пузырьковая сортировка таковыми не являются.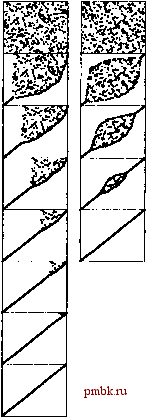

РИСУНОК 6.7. ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ ДВУХ ПУЗЫРЬКОВЫХ СОРТИРОВОК

Стандартная пузырьковая сортировка (слева) работает подобно сортировке выбором в плане того, что каждый проход устанавливает один элемент в его окончательную позицию, но в то же время он асимметрично привносит некоторый порядок в остальную часть массива. Смена направления просмотра массива на альтернативный (т.е. просмотр в направлении с начала до конца массива меняется на обратный и наоборот) порождает новую разновидность пузырьковой сортировки, получившей название шейкер-сортировки (справа), которая заканчивается быстрее (см. упражнение 6.30).

Таблица 6.1. Эмпирические исследования элементарных алгоритмов сортировки

На файлах небольших размеров быстродействие сортировки вставками и выбором примерно в два раза выше, чем у пузырьковой сортировки, но время выполнения этого вида сортировки находится в квадратичной зависимости от размера файла (если размер файла возрастает в 2 раза, то время его сортировки возрастает в 4 раза). Ни