Предположим, что мы всегда передвигаемся по файлу справа налево. Если удается обнаружить минимальный элемент на первом проходе, он меняется местами с каждым элементом, стоящим от него слева, и, в конце концов, этот элемент помещается в позицию на левой границе массива. Затем на втором проходе в соответствующую позицию устанавливается второй по величине элемент и т.д. Таким образом, вполне достаточно выполнить N проходов, т.е., пузырьковую сортировку можно рассматривать как один из видов сортировки выбором, хотя при этом для помещения каждого элемента в соответствующую позицию приходится выполнять больший объем действий. Программа 6.4 представляет собой реализацию алгоритма пузырьковой сортировки, а на рис. 6.4 показан пример работы этого алгоритма.

Программа 6.4. Пузырьковая сортировка

Для каждого i от I до г-1 внутренний цикл (j) помещает минимальный элемент среди элементов

последовательности a[i].....а[г] в a[i], переходя от

элемента к элементу справа налево и выполняя при этом операции сравнения значений соседних элементов и обмена местами следующих друг за другом элементов. Наименьший элемент безпрепятственно перемещается при всех таких операциях сравнения влево и всплывает как и пузырек в начале файла. Как и в случае сортировки методом выбора, в условиях которой индекс i перемещается по файлу слева направо, элементы слева от него находятся в своих окончательных позициях.

template <class Item> void bvibbledtem a[], int 1, int r) { for (int i = 1; i < r; i++) for (int j = r; j > i; j -) compexch(a[j-1] , a[j]);

e X A M P l

G e Х()М P

N G e X(l)M

i n G(l)X

t i n R T(l)n

OR Т(Й)

Г(Й)5 О R Т

L M®S CRT

A S О R Т I N G A®S О R T I N A A(Ds 0 R T i A A E(DS CRT A A E E©S О R A A E E G0S О A A E E G I 0S A A E E G I A A E EG I A A E E G I L M N©S(R AAE EG I LMN0(s;2 AAEEGILMNO P®¥ AAEEGILMNOPR<S A A EEC I I M N О P R S A A E EG Г L M N 0 P R S AAEEG I LMNOPRS

РИСУНОК 6.4. ПРИМЕР ВЫПОЛНЕНИЯ ПУЗЫРЬКОВОЙ СОРТИРОВКИ

в процессе пузырьковой сортировки ключи с малыми значениями устремляются влево. Поскольку сортировка производится в направлении справа налево, каждый ключ меняется местами с ключом слева до тех пор, пока не будет обнаружен ключ с меньшим значением. На первом проходе Е меняется местами с L, Ри М, пока не остановится справа от А; далее уже А продвигается к началу файла, пока не остановится перед другим А, который уже занимает окончательную позицию, i-u по величине ключ устанавливается в свое окончательное положение после i-ого прохода, как и в случае сортировки выбором, но при этом и другие ключи также приближаются к своим окончательным позициям.

Быстродействие программы 6.4 можно повысить за счет экономной реализации внутреннего цикла, выполняя те же приемы, которые применялись в разделе 6.3 при разработке программы сортировки вставками (см. также упражнение 6.25). В самом деле, если сравнивать программные коды, то программа 6.4 оказывается практически идентичной неадаптивной сортировке вставками, реализованной в программе 6.1. Различия между ними состоят в том, что в условиях сортировки вставками внутренний цикл for продвигается вдоль левой (отсортированной) части массива, а в условиях пузырьковой сортировки - вдоль правой (не обязательно отсортированной) части массива.

Программа 6.4 использует только инструкции compexch и по этой причине не является адаптивной реализацией, однако, если файл практически отсортирован, можно заставить ее работать с большей эффективностью, проверяя, не оказался ли очередной проход таким, что на нем не было выполнено ни одной операции перестановки элементов местами (что равносильно полному упорядочению файла, в связи с чем можно покинуть внешний цикл). Внедрение в программу подобного усовершенствования позволяет повысить быстродействие пузырьковой сортировки на некоторых типах файлов, однако в общем случае она не достигнет той эффективности, которая характерна для программы сортировки вставками, в которую внесены изменения, обеспечивающие своевременный выход из внутреннего цикла, о чем подробно рассказывается в разделе 6.5.

Упражнения

> 6.20. В стиле рис. 6.4 показать, как сортируется учебный файл EASYQUES Т I О N методом пузырьковой сортировки.

6.21. Дать пример файла, для которого пузырьковая сортировка выполняет максимально возможное количество перестановок элементов местами.

о 6.22. Является ли пузырьковая сортировка устойчивой?

6.23. Объясните, почему пузырьковая сортировка оказывается более предпочтительной, нежели неадаптивная версия сортировки выбором, описанная в упражнении 6.19.

6.24. Проделайте эксперимент с целью определения, сколько проходов файла с произвольной организацией из элементов экономится в результате добавления в пузырьковую сортировку возможностей прекращения сортировки по результатам проверки, отсортирован файл или нет.

6.25. Разработать эффективную реализацию пузырьковой сортировки с минимально возможным числом команд во внутреннем цикле. Убедиться в том, что проделанные усовершенствования не снижают быстродействия программы!

6.5. Характеристики производительности элементарных методов сортировки

Алгоритмы сортировки выбором, вставками и пузырьковая сортировка по времени выполнения находятся в квадратичной зависимости от числа элементов как в наиболее трудных, так и в обычных случаях, но в то же время они не нуждаются в дополнительной памяти. Таким образом, время их выполнения отличается только постоянным коэффициентом пропорциональности этой зависимости, хотя принципы их работы существенно различаются, о чем свидетельствуют рис. 6.5, 6.6 и 6.7.

В общем случае время выполнения алгоритма сортировки пропорционально количеству операций сравнения, выполняемых этим алгоритмом, количеству перемещений или перемен местами элементов, а, возможно, и обоим сразу. В случае ввода данных, упорядоченных случайным образом, сравнение указанных методов сортировки предполагает изучение различий между соответствующими постоянными коэффициентами пропорциональности в зависимости от числа выполняемых операций

сравнений и перемены сортируемых элементов местами, а также различий соответствующих постоянных коэффициентов пропорциональности в зависимости от числа выполняемых операций во внутренних циклах. В случае ввода данных со специальными характеристиками времена выполнения различных видов сортировок могут отличаться в большей степени, нежели по значениям указанных выше постоянных коэффициентов пропорциональности. В данном разделе подробно рассматриваются аналитические результаты, свидетельствующие в пользу этого заключения.

Лемма 6.1. Сортировка выбором производит примерно N/2 операций сравнения и N операций обмена элементов местами.

Можно легко проверить это свойство на примере данных, приведенных на рис, 6.2, представляющих собой таблицу размерностью Л на Л, на которой незаштрихованные буквы соответствуют сравнениям. Примерно половина элементов этой таблицы не заштрихована, эти элементы расположены над диагональю. Каждому из - 1 элементов (за исключением завершающего элемента) на диагонали соответствует операции обмена. Точнее, исследование программного кода показывает, что на каждое / от 1 до - 1 приходится одна операция обмена и N - i сравнений, так что всего производится 7V - 1 операций обмена и {N - \) + {N- 2)+...+2+\ = N(N - I) / 2 операций сравнения. Эти свойства сохраняются независимо от природы входных данных; единственный показатель сортировки выбором, зависящий от характера входных данных - это число операций присваивания переменной min новых значений. В наихудшем случае эта величина также становится квадратично зависимой, однако в среднем она характеризуется значением 0(Nlo$N) (см. раздел ссылок), так что мы вправе рассчитывать на то, что время выполнения сортировки выбором не чувствительно к природе входных данных.

Лемма 6.2. Сортировка вставками производит в среднем приблизительно N/A операций сравнения и N/A операций полуобмена элементов местами (перемещений) и в два раза больше операций в наихудшем случае.

Сортировка, реализованная программой 6.3, выполняет одно и то же число сравнений и перемещений. Так же как и лемма 6.1, эта величина легко просле-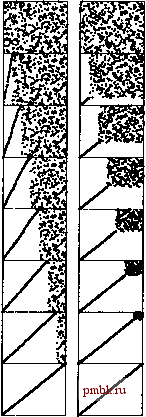

РИСУНОК 6.5. ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ СОРТИРОВОК ВЫБОРОМ И ВСТАВКАМИ

Эти снимки сортировки вставками (слева) и выбором (справа) на примере случайной последовательности иллюстрируют протекание процессов сортировки указанными выше методами. На рисунке процесс сортировки показан в виде графика зависимости afij от i для каждого L Перед началом сортировки на графике представлена равномерно распределенная случайная величина; по окончании сортировки график представлен диагональю, проходящий из левой нижнего угла в правый верхний угол. Сортировка вставками никогда не забегает вперед по отношению к текущей позиции в массиве, в то время как сортировка выбором никогда не возвращается назад.