РИСУНОК 5.35 ДИНАМИКА ОЧЕРЕДИ °

ПОИСКА В ШИРИНУ

075216 075216

7 S216124 7 S2164

5 21612443 5 2164

6124434 643

2 4 4 3 4 4 3

4 4 3 4 3 4 3 4 3

Обработка начинается с узла О в очереди, затем мы получаем узел О, посещаем его и г 1612443 г 1б4з

помещаем в очередь узлы 7 5 2 1 6 из его i 612443 1 б4з

списка смежности, причем именно в этом порядке. Затем мы получаем узел 7, посещаем его и помещаем в очередь узлы из его списка смежности, и т.д. В случае з 4 3

запрета дублирования через стратегию з 4 з

игнорирования нового элемента (справа)

мы получаем такой же результат без наличия каких-либо лишних записей очереди.

Программа 5.22 Поиск в ширину

Чтобы посетить в графе все узлы, связанные с узлом к, к помещается в очередь FIFO, затем выполняется цикл, в котором из очереди получается следующий узел и, если он еще не был посещен, он посещается и в стек заталкиваются все непосещенные узлы из его списка смежности; процесс продолжается до тех пор, пока очередь не опустеет.

void traverse(int к, void visit(int)) {

QUEUE<int> q(V*V); q.put(k);

while (! q. empty() )

if (visited[k = q.get()] == 0)

visit(k); visited[k] = 1;

for (link t = adjtk]; t =0; t = t->next) if (visited[t->v] == 0) q.put(t->v) ;

При использовании обоих методов поиска в ширину и в глубину посешаются все узлы графа, но их способ достижения этого различается коренным образом, что демонстрирует рис. 5.36. Поиск в ширину подобен армии исследователей, разосланной во все стороны с целью охвата всей территории; поиск в глубину соответствует единственному исследователю, который как можно дальше проникает вглубь неизведанной территории, возвращаясь только в случае, если наталкивается на тупик. Таковы базовые методы решения задач, играющие существенную роль во многих областях компьютерных наук, а не только в контексте поиска в графах.

Упражнения

5.92 Принимая во внимание диафаммы, соответствующие рис. 5.33 (слева) и 5.34 (справа), покажите, как происходит посещение узлов в графе, построенном для последовательности ребер 0-2, 1-4, 2-5, 3-6, 0-4, 6-0 и 1-3 (см. упражнение 3.70), при рекурсивном поиске в глубину.

5.93 Принимая во внимание диафаммы, соответствующие рис. 5.33 (слева) и 5.34 (справа), покажите, как происходит посещение узлов в графе, построенном для

последовательности ребер 0-2, 1-4, 2-5, 3-6, 0-4, 6-0 и 1-3 (см, упражнение 3.70), при поиске в глубину с использованием стека,

5.94 Принимая во внимание диаграммы, соответствующие рис, 5,33 (слева) и 5.35 (справа), покажите, как происходит посещение узлов в графе, построенном для последовательности ребер 0-2, 1-4, 2-5, 3-6, 0-4, 6-0 и 1-3 (см. упражнение 3.70), при поиске в ширину (с ncnojjb-зованием очереди).

о 5.95 Почему время выполнения, упоминаемое в лемме 5.10, пропорционально К + а не просто Е1

5.96 Принимая во внимание диаграммы, соответствующие рис. 5.33 (слева) и 5.35 (справа), покажите, как происходит посещение узлов в примере графа, приведенном в тексте (рис.3.15), при поиске в глубину с использованием стека с применением стратегии забывания старого элемента .

5.97 Принимая во внимание диаграммы, соответствующие рис. 5,33 (слева) и 5,35 (справа), покажите, как происходит посещение узлов в примере графа, приведенном в тексте (рис.3.15), при поиске в глубину с использованием стека с применением стратегии игнорирования нового элемента .

[> 5.98 Реализуйте поиск в глубину с использованием стека для графов, которые представлены списками смежности.

о 5.99 Реализуйте рекурсивный поиск в глубину для графов, которые представлены списками смежности.

5.9 Перспективы

Рекурсия лежит в основе ранних теоретических исследований природы вычислений. Рекурсивные функции и программы играют главную роль в математических исследованиях, в которых предпринимается попытка разделения задач на поддающиеся решению на компьютере и на непригодные для этого,

В ходе столь краткого рассмотрения просто невозможно полностью осветить столь обширные темы, как деревья и рекурсия. Многие наиболее показательные примеры рекурсивных программ будут пребывать в центре внимания на протяжении всей книги - к ним относятся алгоритмы типа разделяй и властвуй и рекурсивные структуры данных, которые успешно применяются для решения широкого спектра задач. Для многих приложений нет смысла вы-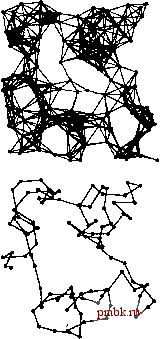

РИСУНОК 5.36 ДЕРЕВЬЯ ОБХОДА ГРАФОВ

На этой схеме показаны поиск в глубину (в центре) и поиск в ширину (внизу), выполненные на половину в большом графе (вверху). При поиске в глубину обход выполняется от одного узла к следующему, так что большинство узлов связано только с двумя другими. И напротив, при поиске в ширину перемещение по графу выполняется по всей области графа, с посещением всех узлов, связанных с данным, прежде чем двигаться дальше; поэтому некоторые узлы связаны со множеством других.

ходить за рамки простой непосредственной рекурсивной реализации; для других будут рассматриваться методы, производные от альтернативных нерекурсивных и восходящих реализаций.

В этой книге основное внимание уделено практическим аспектам построения рекурсивных программ и структур данных. Наша цель - применение рекурсии для создания изящных и эффективных реализаций. Для дрстижения этой цели необходимо особо учитывать опасности, сопряженные с использованием простых программ, которое ведет к экспоненциальному увеличению количества вызовов функций или недопустимо большой степени вложенности. Несмотря на этот недостаток, рекурсивные программы и структуры данных весьма привлекательны, поскольку часто они предоставляют индуктивные аргументы, которые помогают убедиться в правильности и эффективности разработанных программ.

На протяжении всей книги деревья используются как для упрощения понимания динамических свойств программ, так и в качестве динамических структур данных. В главах с 12 по 15 особенно большое внимание уделяется манипулированию явными древовидными структурами. Свойства, описанные в этой главе, предоставляют основную информацию, которая требуется для эффективного применения явных древовидных структур.

Несмотря на свою центральную роль в разработке алгоритмов, рекурсия - вовсе не панацея на все случаи жизни. Как было показано при исследовании алгоритмов обхода деревьев и графов, алгоритмы с использованием стека (которые рекурсивны по своей природе) - не единственная возможность при необходимости управлять задачами с множеством вычислений. Эффективная технология разработки алгоритмов для решения многих задач заключается в использовании обобщенных реализаций с применением очередей, отличающихся от стеков, которые предоставляют свободу выбирать следующую задачу в соответствии с каким-либо более субъективным критерием, нежели простой выбор чего-либо последнего. Структуры данных и алгоритмы, которые эффективно поддерживают такие операции - основная тема главы 9, а со многими примерами их применения мы встретимся во время исследования алгоритмов обработки графов в части 7.

Ссылки для чааи 2

Существует множество учебников для начинающих, посвященных структурам данных. Например, в книге Стендиша (Standish) темы связных структур, абстракций данных, стеков и очередей, распределения памяти и создания программ освещаются более подробно, чем здесь. Конечно, классические книги Кернигана и Ритчи (Kernighan-Ritchie) и Страуструпа (Stroustrup) - бесценные источники подробной информации по реализациям С и С++. Книги Мейерса (Meyers) также содержат полезную информацию о реализациях С++.

Разработчики PostScript, вероятно, не могли даже и предполагать, что разработанный ими язык будет представлять интерес для людей, которые изучают основы алгоритмов и структур данных. Сам по себе этот язык не представляет особой сложности, а справочные руководства по нему - основательны и доступны.