РИСУНОК 5.33 ПОИСК в ГЛУБИНУ И ПОИСК в ШИРИНУ

При поиске в глубину (слева) переход выполняется от узла к узлу, с возвратом к предшествующему узлу с целью проверки следующей возможности, когда все соседние связи данного узла проверены. При поиске в ширину (справа), до перехода к следующему узлу сначала должны быть перебраны все возможности для данного узла.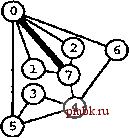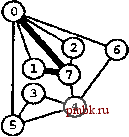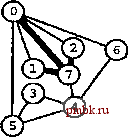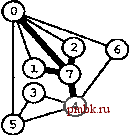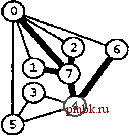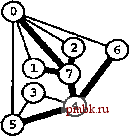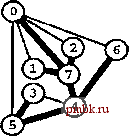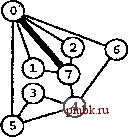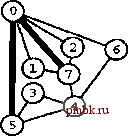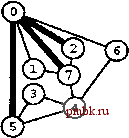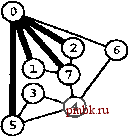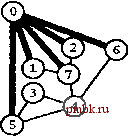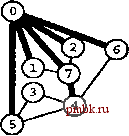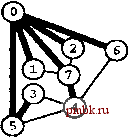

шине графа соответствует один указатель на начало списка. Поиск в глубину затрагивает каждый из них не более одного раза.

Поскольку время, необходимое для построения представления в виде списков смежности из последовательности ребер (см. программу 3.19), также пропорционально V + Е, поиск в глубину обеспечивает линейное по отношению к затрачиваемому времени решение задачи связности из главы 1. Однако для очень больших графов решения union-find все же могут оказаться предпочтительнее, поскольку для представления всего графа требуется объем памяти, пропорциональный Е, в то время как для решений union-find необходим объем памяти, который пропорционален только V.

Подобно тому как это было сделано в случае с обходом дерева, можно определить метод обхода графа, при котором используется явный стек, как показано на рис. 5.34. Моно представить себе абстрактный стек, содержащий двойные записи: узел и указатель на список смежности для этого узла. Когда стек инициализируется начальным узлом, а указатель - первым элементом списка смежности для этого узла, алгоритм поиска в глубину эквивалентен входу в цикл, в котором сначала посещается узел в верхней части стека (если он еще не был посещен); затем сохраняется узел, указанный текущим указателем списка смежности; далее, ссылка из списка смежности обновляется следующим узлом (с выталкиванием записи, если достигнут конец списка смежности); и, наконец, запись стека для сохраненного узла заталкивается со ссылкой на первый узел его списка смежности.

РИСУНОК 5.34 ДИНАМИКА СТЕКА ПОИСКА В ГЛУБИНУ

Стек, поддерживающий поиск в глубину, можно представить себе как содержащий узел и ссылку на список смежности для этого узла (он показан узлом, заключенным в окружность) (слева). Таким образом, обработка в стеке начинается с узла О, т.е. со ссылки на первый узел в его списке смежности - узел 7. Каждая строка отражает результат выталкивания из стека, занесения ссылки на следующий узел в списке посещенных узлов и занесения в стек записи для непосещенных узлов. Процесс также можно предстаёить в виде простого заталкивания в стек всех узлов, смежных с любым непосещенным узлом (справа).

7 1 7 О 2 7 О О 4 6 4 О S О 4 3 5 4 7 3 5 1 2 6

Или же, подобно тому, как это было сделано для обхода дерева, можно создать стек, содержащий только ссылки на узлы. Когда стек инициализируется начальным узлом, мы входим в цикл, в котором посещаем узел в верхней части стека (если он еще не был посещен), затем заталкиваем в стек все соседние узлы этого узла. Рисунок 5.34 иллюстрирует, что для нашего примера графа оба метода эквивалентны поиску в глубину, причем эквивалентность сохраняется и в общем случае.

Алгоритм посещения верхнего узла и заталкивания всех его соседей - простая формулировка поиска в глубину, но из рис. 5.34 понятно, что этому метод присущ недостаток возможного оставления в стеке нескольких копий каждого узла. Это происходит даже в случае проверки, посещался ли каждый узел, который должен быть помещен в стек, и если да, то отказа от занесения в стек такого узла. Во избежание упомянутой проблемы можно воспользоваться реализацией стека, которая запрещает дублирование за счет применения стратегии забывания старого элемента : поскольку ближайшая к верхушке стека копия всегда посещается первой, все остальные копии просто выталкиваются из стека.

Динамика состояния стека для поиска в глубину, показанная на рис. 5.34, основана на том, что узлы каждого списка соседних узлов появляются в стеке в том же порядке, что и в списке. Для получения этого порядка для данного списка смежности при заталкивании узлов по одному, вначале следовало бы затолкнуть в стек последний узел, затем предпоследний и т.д. Более того, чтобы ограничить размер стека числом вершин при одновременном посещении узлов в том же порядке, как и при поиске в глубину, необходимо использовать стек, в котором реализуется стратегия забывания старого элемента . Если посещение узлов в том же порядке, что и при поиске в глубину, не имеет значения, обоих этих осложнений можно избежать и непосредственно сформулировать нерекурсивный метод обхода графа с использованием стека, который выглядит так. После инициализации стека начальным узлом мы входим в цикл, в котором посещаем узел на верхушке стека, затем обрабатываем его список смежности, помещая в стек каждый узел (если он еще не был посещен) и используя реализацию стека, которая за счет применения стратегии игнорирования нового элемента запрещает дублирование. Этот алгоритм обеспечивает посещение всех узлов графа, подобно поиску в глубину, но не является рекурсивным.

Алгоритм, описанный в предыдущем абзаце, заслуживает внимания, поскольку можно было бы воспользоваться любым обобщенным абстрактным типом данных очереди и все же посетить каждый из узлов графа (плюс сгенерировать развернутое дерево). Например, если вместо стека задействовать очередь, то получится поиск в ширину, который аналогичен обходу дерева по уровням. Программа 5.22 - реализация этого метода (при условии, что используется реализация с применением очереди, подобная программе 4.12); пример этого алгоритма в действии показан на рис. 5.35. В части 6 будет исследоваться множество алгоритмов обработки графов, основанных на более сложных обобщенных абстрактных типах данных очереди.