Действительно, реализации с использованием деревьев для нескольких из обобщенных абстрактных типов данных (ATD) запросов, рассмотренных в разделе 4.6, относятся к основной теме большей части этой книги. В частности, многие из алгоритмов, приведенных в главах 12-15, основываются на деревьях бинарного поиска (binary search tree), которые являются явными деревьями, соответствующими бинарному поиску, аналогично тому, как явная структура на рис. 5.30 взаимосвязана с рекурсивным алгоритмом отыскания максимума (см. рис. 5.6). Сложность реализации и использования таких структур заключается в обеспечении эффективности алгоритмов после выполнения большого числа операций вставки, удаления и других операций.

Вторым примером программы создания бинарного дерева служит измененная версия программы оценки префиксного выражения, приведенной в разделе 5.1 (программа 5.4), которая создает дерево, представляющее префиксное выражение, а не просто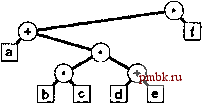

РИСУНОК 5.31 ДЕРЕВО СИНТАКСИЧЕСКОГО АНАЛИЗА

Это дерево создается программой 5.20 для префиксного выражения * + a**bc + def. Оно представляет собой естественный метод представления выражения: каждый операнд размещается в листе (который отображен в качестве внешнего узла), а каждая операция, которая должна применяться к выражению, представлена левым и правым поддеревьями узла, содержащего операцию.

оценивает его (см. рис. 5.31). В программе 5.20 используется та же рекурсивная схема, что и в программе 5.4, но рекурсивная функция возвращает ссылку на дерево, а не значение. Программа создает новый узел дерева для каждого символа в выражении: узлы, которые соответствуют операциям, имеют связи со своими операндами, а узлы листьев содержат переменные (или константы), которые являются входными данными выражения.

Программа 5.20 Создание дерева синтаксического анализа

Используй ту же стратегию, которая была задействована при оценке префиксных выражений (см. программу 5.4), эта программа создает дерево синтаксического анализа из префиксного выражения. Для простоты предполагается, что операндами являются одиночные символы. Каждый вызов рекурсивной функции создает новый узел, передавая в него в качестве лексемы следующий символ из массива входных данных. Если лексема представляет собой операнд, программа возвращает новый узел, а если операция - то устанавливает левый и правый указатели на дерево, построенное (рекурсивно) для двух аргументов.

char *а; int i; struct node

{ Item item; node *1,

node(Item x)

{ item = x; 1 = 0; r = 0; }

typedef node* link; link parse 0 { char t = a[i++]; link x = new node(t); if ((t -= + ) II (t == *))

{ x->l = parse (); x->r = parse (); } return x;

В программах трансляции, подобных компиляторам, часто используются такие внутренние представления программ в виде деревьев, поскольку деревья удобны для достижения многих целей. Например, можно представить операнд, соответствующие переменным, принимающим значения, и сгенерировать мащинный код для оценки выражения, представленного в виде дерева с обратным обходом. Либо же можно воспользоваться деревом с поперечным обходом для вывода выражения в инфиксной форме или дерево с обратным обходом - для вывода выражения в постфиксной форме.

В этом разделе было рассмотрено несколько примеров, подтверждающих концепцию о возможности создания и обработки структур явных связных деревьев с помощью рекурсивных программ. Чтобы этот подход стал эффективным, потребуется учесть производительность различных алгоритмов, альтернативные представления, нерекурсивные альтернативы и ряд других нюансов. Однако, более подробное рассмотрение программ обработки деревьев откладывается до главы 12, поскольку в главах 7-11 деревья используются, в основном, в описательных целях. К реализациям явных деревьев мы вернемся в главе 12, поскольку они служат основой для многих алгоритмов, исследуемых в главах 12-15.

Упражнения

о 5.85 Измените программу 5.18, чтобы она выводила PostScript-программу, которая рисует дерево в формате, подобном использованному на рис. 5.23, но без маленьких квадратов, представляющих внешние узлы. Используйте операторы moveto и lineto для рисования линий и оператор

/node {newpath moveto currentpoint 4 О 360 arc fill} def

ДЛЯ рисования узлов. После инициализации этого определения вызов node приводит к рисованию черной точки в точке с координатами, помещенными в стек (см. раздел 4.3).

о 5.86 Создайте программу, которая подсчитывает листья в бинарном дереве.

о 5.87 Создайте программу, которая подсчитывает количество узлов в бинарном дереве с одним внешним и одним внутренним дочерними деревьями.

о 5.88 Создайте рекурсивную программу, которая вычисляет длину внутреннего пути бинарного дерева, используя определение 5.6.

5.89 Определите количество вызовов функций, выполненных программой при вычислении длины внутреннего пути бинарного дерева. Докажите ответ методом индукции.

5.90 Создайте рекурсивную программу, которая вычисляет длину внутреннего пути бинарного дерева за время, которое пропорционально количеству узлов в дереве.

о 5.91 Создайте рекурсивную программу, которая удаляет из турнира все листья с заданным ключом (см. упражнение 5.59).

5.8 Обход графа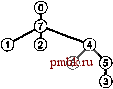

в качестве заключительного примера в этой главе рассмотрим одну из наиболее важных рекурсивных профамм: рекурсивный обход фафа, или поиск в глубину (depth-first search). Этот метод симметричного посещения всех узлов графа - непосредственное обобщение методов обхода деревьев, рассмотренных в разделе 5.6, и он служит основой для многих базовых алгоритмов обработки фафов (см. часть 7). Это простой рекурсивный алгоритм. Начиная с любого узла v, мы

посещаем v;

(рекурсивно) посещаем каждый {непосещенный) узел, связанный с v.

Если граф является связным, со временем будут посещены все узлы. Программа 5.21 демонстрирует реализацию этой рекурсивной процедуры.

Профамма 5.21 Поиск в глубину

Для посещения в графе всех узлов, связанных с узлом к, мы помечаем его как посещенный, а затем (рекурсивно) посещаем все непосещенные узлы в списке смежности для узла к.

void traverse(int к, void visit(int)) { visit(к); visited[к] = 1;

for (link t = adj[k]; t = 0; t = t->next) if (!visited[t->v]) traverse(t->v, visit);

Например, предположим, что используется представление в виде списка соседних узлов, описанное в примере фафа на рис. 3.15. На рис. 5.32 показаны последовательность вызовов, выполненных при поиске в глубину в этом фафе, а последовательность прохождения ребер графа находится в левой части рис. 5.33. При прохождении каждого из ребер графа возможны два исхода: если ребро приводит к уже посещенному узлу, мы игнорируем его; если оно приводит к еще не посещенному узлу, мы переходим к нему через рекурсивный вызов. Набор всех просмотренных таким образом ребер образует остовное дерево графа.

Различие между поиском в глубину и общим обходом дерева (см. программу 5.14) состоит в том, что необходимо явно исключить посещение уже посещенных узлов. В дереве мы никогда не встречаемся с такими узлами. Действительно, если граф является деревом, рекурсивный поиск в глубину, начинающийся с корня, эквивалентен прямому обходу.

Лемма 5.10 Время, требующееся для выполнения поиска в глубину в графе с V вершинами и Е ребрами, пропорционально V + Е, если использовать представление графа в виде списков смежности.

В представлении в виде списков смежности каждому ребру графа соответствует один узел в списке, а каждой вер-

visit О

visit 7 (first on Os list) visit 1 (first on 7s list) check 7 on 1 s list checl 0 on 1 s list visit 2 (second on 7s list) check 7 on 2s list check 0 on 2s list check 0 on 7s list visit 4 (fourth on 7s list) visit 6 (first on 4s list) check 4 on 6s list check 0 on 6s list visit 5 (second on 4s list) check 0 on 5s list check 4 on 5s list visit 3 (third on 5 s list) check 5 on 3s list check 4 on 3s list check 7 on 4s list check 3 on 4s list check 5 on Os list check 2 on Os list check 1 on Os list check 6 on Os list

РИСУНОК 5.32 ВЫЗОВЫ ФУНКЦИЙ ПОИСКА В ГЛУБИНУ

Эта последовательность вызовов функций реализует поиск в глубину для примера графа, приведенного на рис. 3.15. Дерево, которое описывает структуру рекурсивных вызовов (вверху), называется деревом поиска в глубину.

Распечатано nporpaHHoii FinePnnt - Купитылулу finepnnt с(