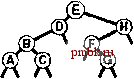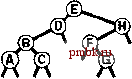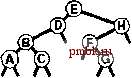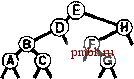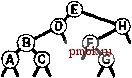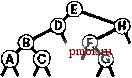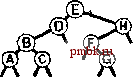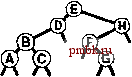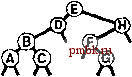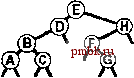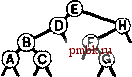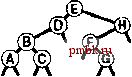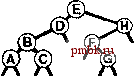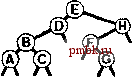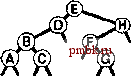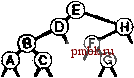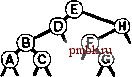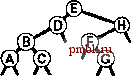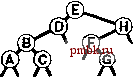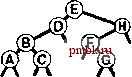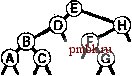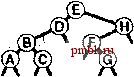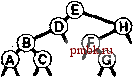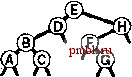РИСУНОК 5.26 ПОРЯДКИ ОБХОДА ДЕРЕВА

Эти последовательности показывают порядок посещения узлов для прямого (слева), поперечного (в центре) и обратного (справа) обхода дерева.

РИСУНОК 5.27 СОДЕРЖИМОЕ СТЕКА ДЛЯ АЛГОРИТМОВ ОБХОДА ДЕРЕВА

Эти последовательности отражают содержимое стека для прямого (слева), поперечного (в центре) и обратного (справа) обхода дерева (см. рис. 5.26) для идеализированной модели вычислений, аналогичной использованной в примере на рис. 5.5, когда элемент и два его поддерева помещаются в стек в указанном порядке.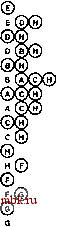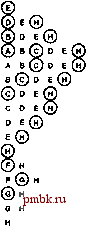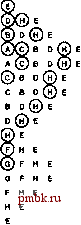

Описанная в предыдущем абзаце схема является концептуальной, охватывающей три метода обхода дерева, однако реализации, используемые на практике, несколько проще. Например, для выполнения прямого обхода не обязательно заталкивать узлы в стек (мы посещаем корень каждого выталкиваемого дерева), поэтому можно воспользоваться простым стеком, состоящим только из одного типа элементов (связей дерева), как это сделано в нерекурсивной реализации в программе 5.15. Системный стек, поддерживающий рекурсивную профамму, содержит адреса возврата и значения аргументов, а не элементы или узлы, но фактическая последовательность выполнения вычислений (посещения узлов) остается одинаковой для рекурсивного метода и метода с использованием стека.

Программа 5.15 Прямой обход (нерекурсивная реализация)

Эта нерекурсивная функция с использованием стека - функциональный эквивалент ее рекурсивного аналога, программы 5.14.

void traverse(link h, void visit(link)) { STACK<link> s(max); s.push(h); while ( s . en5)ty ()) {

visit(h = s.popO) ;

if (h->r != 0) s.push(h->r) ;

if (h->l != 0) s.push(h->l) ;

Четвертая естественная стратегия обхода - простое посещение узлов дерева в порядке, в котором они отображаются на странице - сверху вниз и слева направо. Этот метод называется обходом по уровням, поскольку все узлы каждого уровня посещаются вместе, по порядку. Посещение узлов дерева, показанного на рис, 5.26, при обходе по уровням показано на рис. 5.28.

Как ни удивительно, обход по уровням можно получить, заменив в программе 5.15 стек очередью, что демонстрирует профамма 5.16. Для реализации прямого обхода используется структура данных типа последним вошел, первым вышел (L1F0); для реализации обхода по уровням используется структура данных типа первым вошел, первым вышел (FIFO). Эти программы заслуживают внимательного изучения.

поскольку они представляют существенно различающиеся подходы к организации остающейся невыполненной работы. В частности, обход по уровням не соответствует рекурсивной реализации, связанной с рекурсивной структурой дерева.

Программа 5.16 Обход по уровням

Изменение структуры данных, лежащей в основе прямого обхода (см. программу 5.15) со стека на очередь приводит к преобразованию обхода в обход по уровням.

void traverse(link h, void visit(link)) { QUEUE<link> q(max) ; q.put(h);

while (iq.einpty 0 ) {

visit (h = q.getO) ;

if (h->l = 0) q.put(h->l);

if (h->r = 0) q.put(h->r);

Прямой обход, обратный обход и обход по уровням однозначно определяются и для боров. Чтобы определения были единообразными, представьте себе бор в виде дерева с воображаемым корнем. Тогда правило для прямого обхода формулируется следующим образом: посетить корень, а затем каждое из поддеревьев ; а правило для обратного обхода - посетить каждое из поддеревьев, а затем корень . Правило для обхода по уровням то же, что и для бинарных деревьев. Непосредственные реализации этих методов - простые обобщения программ прямого обхода с использованием стека (программы 5.14 и 5.15) и программы обхода по уровням с использованием очереди (программа 5.16) для бинарных деревьев, которые мы только что рассмотрели. Соображения по поводу реализаций не приводятся, поскольку в разделе 5.8 мы рассмотрели более общую проце-

ДУРУ-

Упражнения

> 5.79 Приведите порядок посещения узлов для прямого, поперечного, обратного и обхода по уровням для следующих бинарных деревьев: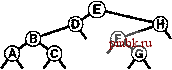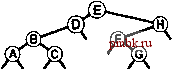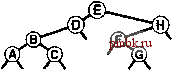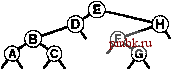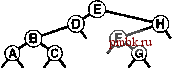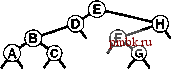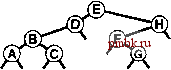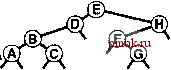

РИСУНОК 5.28 ОБХОД ПО УРОВНЯМ

Эта последовательность отображает результат посещения узлов дерева в порядке сверху вниз и слева направо.

t> 5.80 Отразите содержимое очереди во время обхода по уровням (программа 5.16) на рис. 5.28, аналогично показанному на рис. 5.27.