Опредление 5.2 М-арное дерево - это внешний узел, либо внутренний узел, связанный с упорядоченной последовательностью М деревьев, которые также являются М-ар-ными деревьями.

Обычно узлы в М-арных деревьях представляются либо в виде структур с М именованными связями (как в бинарных деревьях), либо в виде массивов М связей. Например, в главе 15 рассмотрены 3-арные (или троичные) деревья, в которых используются структуры с тремя именованными связями (левой, средней и правой), каждая из которых имеет специальное значение для связанных с ними алгоритмов. В остальных случаях использование массивов для хранения связей вполне подходит, поскольку значение М фиксировано, хотя, как будет показано, при использовании такого представления особое внимание потребуется уделить интенсивному использованию памяти.

Определение 5.3 Дерево (также называемое упорядоченным деревом) - это узел (называемый корнем), связанный с последовательностью несвязанных деревьев. Такая последовательность называется бором.

Различие между упорядоченными деревьями и М-арными деревьями состоит в том, что узлы в упорядоченных деревьях могут иметь любое количество дочерних узлов, в то время как узлы в Л/-арных деревьях должны иметь точно М дочерних узлов. Иногда в контекстах, в которых требуется различать упорядоченные и Л/-арные деревья, мы используем термин главное дерево (general tree).

Поскольку каждый узел в упорядоченном дереве может иметь любое количество связей, представляется естественным рассматривать его с использованием связного списка, а не массива, для хранения связей с дочерними узлами. Пример такого представления приведен на рис. 5.22. Из этого примера видно, что тогда каждый узел содержит две связи: одну для связного списка, соединяющего его с родственными узлами, и вторую для связного списка его дочерних узлов.

Лемма 5.4 Существует однозначное соответствие между бинарными деревьями и упорядоченными борами.

Это соответствие показано на рис. 5.22. Любой бор можно представить в виде бинарного дерева, сделав левую связь каждого узла указывающей на его левый дочерний узел, а правую связь каждого узла - указывающей на родственный узел, расположенный справа.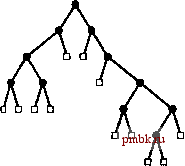

г-am ЕПЕп

azE]

РИСУНОК 5.21 ПРЕДСТАВЛЕНИЕ БИНАРНОГО ДЕРЕВА

В стандартном представлении бинарного дерева используются узлы с двумя связями: левой связью с левым поддеревом и правой связью с правым поддеревом. Нулевые связи соответствуют внешним узлам.

Определение 5.4 Дерево с корнем (или неупорядоченное дерево) - это узел (называемый корнем), связанный с множественным набором деревьев с корнем. (Такой множественный набор называется неупорядоченным бором.)

Деревья, с которыми мы встречались в главе 1, посвященной проблеме связности, являются неупорядоченными деревьями. Такие деревья могут быть определены в качестве упорядоченных деревьев, в которых порядок рассмотрения дочерних узлов узла не имеет значения. Неупорядоченные деревья можно было бы также определить в виде набора взаимосвязей между родительскими и дочерними узлами. Такое представление может казаться не связанным с рассматриваемыми рекурсивными структурами, но, вероятно, является конкретным представлением, которое в основном соответствует абстрактному подходу.

Неупорядоченное дерево можно было бы представить в компьютере упорядоченным деревом; при этом приходится признать, что несколько различных упорядоченных деревьев могут представлять одно и то же неупорядоченное дерево. Действительно, обратная задача определения того, представляют ли два различные упорядоченные дерева одно и то же неупорядоченное дерево (задача изоморфизма дерева) трудно подается рещению.

Наиболее общим типом деревьев является дерево, в котором не выделен ни один корневой узел. Например, остовные деревья, полученные в результате работы алгоритмов связности из главы 1, обладают этим свойством. Для правильного определения деревьев без корня, неупорядоченных деревьев и свободных деревьев потребуется начать с определения графов (graphs).

Определение 5.5 Граф - это набор узлов с набором ребер, которые соединяют пары отдельных узлов (причем любую пару узлов соединяет только одно ребро).

£

rSTE--ще--гш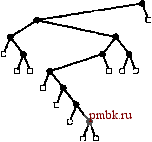

ГТТ1 I-FTTI EO

РИСУНОК 5.22 ПРЕДСТАВЛЕНИЕ ДЕРЕВА

Представление упорядоченного дерева за счет поддержания связного списка дочерних узлов каждого узла эквивалентно представлению его в виде двоичного дерева. На схеме справа вверху показано представление в виде связного списка дочерних узлов для дерева, показанного слева вверху; при этом список реализован в правых связях узлов, а левая связь каждого узла указывает на первый узел в связном списке его дочерних узлов. На схеме справа внизу приведена несколько измененная версия верхней схемы; она представляет бинарное дерево, изображенное слева внизу. Таким образом, бинарное дерево можно рассматривать в качестве представления дерева.

Представьте себе, что перемещаетесь вдоль ребра от одного какого-либо узла до другого, затем от этого узла к следующему и т.д. Последовательность ребер, ведущих от одного узла до другого, когда ни один узел не посещается дважды, называется простым путем. Граф является связным (connected), если существует простой путь, связывающий любую пару узлов. Простой путь, у которого первый и последний узел совпадают, называется циклом (cycle).

Каждое дерево является графом; а какие же фафы являются деревьями? Граф считается деревом, если он удовлетворяет любому из следующих четырех условий:

Граф имеет Л- 1 ребер и ни одного цикла.

Граф имеет N- 1 ребер и является связным.

Только один простой путь соединяет каждую пару вершин в графе.

Граф является связным, но перестает быть таковым при удалении любого ребра.

Любое из этих условий - необходимое и достаточное условие для выполнения остальных трех. Формально, одно из них должно было бы служить определением свободного дерева; неформально, они все вместе служат определением.

Мы представляем свободное дерево в виде коллекции ребер. Если представлять свободное дерево неупорядоченным, упорядоченным или даже бинарным деревом, придется признать, что в общем случае существует множество различных способов представления каждого свободного дерева.

Абстракция дерева используется часто, и рассмотренные в этом разделе различия важны, поскольку знание различных абстракций деревьев - существенная составляющая определения эффективного алгоритма и соответствующих структур данных для решения данной задачи. Часто приходится работать непосредственно с конкретными представлениями деревьев без учета конкретной абстракции, но в то же время часто имеет смысл поработать с соответствующей абстракцией дерева, а затем рассмотреть различные конкретные представления. В книге приведено множество примеров этого процесса.

Прежде чем вернуться к алгоритмам и представлениям, мы рассмотрим ряд основных математических свойств деревьев; эти свойства будут использоваться при разработке и анализе алгоритмов в виде деревьев.

Упражнения

> 5.56 Приведите представления свободного дерева, показанного на рис. 5.20, в форме дерева с корнем и бинарного дерева.

t 5.57 Сколько существует различных способов представления свободного дерева, показанного на рис. 5.20, в форме упорядоченного дерева?

> 5.58 Нарисуйте три упорядоченных дерева, которые изоморфны по отношению к упорядоченному дереву, показанному на рис. 5.20. Другими словами, должна существовать возможность преобразования всех четырех деревьев одного в другое путем обмена дочерними узлами.

о 5.59 Предположите, что деревья содержат элементы, для которых определена операция operator==. Создайте рекурсивную программу, которая удаляет в бинарном дереве все листья, содержащие элементы, равные данному (см. программу 5.5).