внутренний узел

РИСУНОК 5.20 ТИПЫ ДЕРЕВЬЕВ

На этих схемах приведены примеры двоичного дерева (вверху слева), троичного дерева (вверху справа), дерева с корнем (внизу слева) и свободного дерева (внизу справа).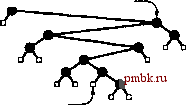

корень

лист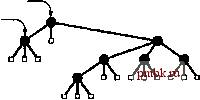

внешний узел

родительский

узел

родственный узел

дочерний узел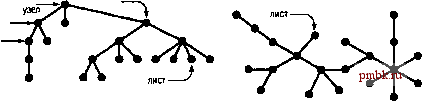

Дерево с корнем (единственным, rooted) - это дерево, в котором один узел назначен корнем (root) дерева. В области компьютеров термин дерево обычно применяется к деревьям с корнем, а термин свободное дерево (free tree) - к более общим структурам, описанным в предыдущем абзаце. В дереве с корнем любой узел является корнем поддерева, состоящего из него и расположенных под ним узлов.

Существует только один путь между корнем и каждым из других узлов дерева. Данное определение никак не определяет направление ребер; обычно считается, что все ребра указывают от корня или к корню, в зависимости от приложения. Обычно деревья с корнем рисуются с корнем, расположенным в верхней части (хотя на первый взгляд это соглащение кажется неестественным), и говорят, что узел у располагается под узлом x (а x располагается над у), если х находится на пути от к корню (т.е., у находится под х, как нарисовано на странице, и соединяется с х путем, который не проходит через корень). Каждый узел (за исключением корня) имеет только один узел над ним, который называется его родительским узлом (parent); узлы, расположенные непосредственно под данным узлом, называются его дочерними узлами (children). Иногда аналогия с генеалогическими деревьями расширяется еще больше и тогда говорят об узлах-предках (grand parent) или родственных (sibling) узлах данного узла.

Узлы, не имеющие дочерних узлов, называются листьями (leaves) или терминальными (оконечными, terminal) узлами. Для соответствия с последним применением узлы, имеющие хотя бы один дочерний узел, иногда называются нетерминальными (nonterminal) узлами. В этой главе мы уже встречались с примером утилиты, различающей эти типы узлов. В деревьях, которые использовались для представления структуры вызовов рекурсивных алгоритмов (например, рис. 5.14), нетерминальные узлы (окружности) представляют вызовы функций с рекурсивными вызовами, а терминальные узлы (квадраты) представляют вызовы функций без рекурсивных вызовов.

В определенных приложениях способ упорядочения дочерних узлов каждого узла имеет значение; в других это не важно. Упорядоченное (ordered) дерево - это дерево с корнем, в котором определен порядок следования дочерних узлов каждого узла. Упорядоченные деревья - естественное представление: например, при рисовании дерева дочерние узлы размещаются в определенном порядке. Действительно, многие тругие конкретные представления имеют аналогично предполагаемый порядок; на-

пример, обычно это различие имеет значение при рассмотрении представления деревьев в компьютере.

Если каждый узел должен иметь конкретное количество дочерних узлов, появляющихся в конкретном порядке, мы имеем М-арное дерево. В таком дереве часто можно определить специальные внешние узлы, которые не имеют дочерних узлов. Тогда внешние узлы могут действовать в качестве фиктивных, на которые ссылаются узлы, не имеющие указанного количества дочерних узлов. В частности, простейшим типом Л/-арного дерева является бинарное дерево. Бинарное дерево (binary tree) - это упорядоченное дерево, состоящее из узлов двух типов: внешних узлов без дочерних узлов и внутренних узлов, каждый из которых имеет ровно два дочерних узла. Поскольку два дочерних узла каждого внутреннего узла упорядочены, говорят о левом дочернем узле (left child) и правом дочернем узле (right child) внутренних узлов. Каждый внутренний узел должен иметь и левый, и правый дочерние узлы, хотя один из них или оба могут быть внешними узлами. Лист в Л/-арном дереве - это внутренний узел, все дочерние узлы которого являются внешними.

Все это общая терминология. Далее рассматриваются формальные определения, представления и приложения, в порядке расширения понятий:

бинарные и М-арные деревья

упорядоченные деревья

деревья с корнем

свободные деревья

Начав с наиболее характерной абстрактной структуры, мы должны быть в состоянии подробно рассмотреть конкретные представления, как станет понятно из дальнейшего изложения.

Определение 5.1 Бинарное дерево - это либо внешний узел, либо внутренний узел, связанный с парой бинарных деревьев, которые называются левым и правым поддеревьями этого узла.

Из этого определения становится понятно, что сами деревья - абстрактное математическое понятие. При работе с компьютерными представлениями мы работаем всего лишь с одной конкретной реализацией этой абстракции. Эта ситуация не отличается от представления действительных чисел значениями типа float, целых чисел значениями типа int и т.д. Когда мы рисуем дерево с узлом в корне, связанным ребрами с левым поддеревом, расположенным слева, и с правым поддеревом, расположенным справа, то выбираем удобное конкретное представление. Существует множество различных способов представления бинарных деревьев (см., например, упражнение 5.62), которые поначалу кажутся удивительными, но вполне отражают сущность, как и можно было ожидать, учитывая абстрактный характер определения.

Чаще всего применяется следующее конкретное представление при реализации программ, использующих и манипулирующих бинарными деревьями, - структура с двумя связями (правой и левой) для внутренних узлов (см. рис. 5.21). Эти структуры аналогичны связным спискам, но они имеют по две связи для каждого узла, а не по одной. Нулевые связи соответствуют внешним узлам. В частности, мы добавили связь

к стандартному представлению связного списка, приведенному в разделе 3.3, следующим образом:

struct node { Item item; node *1, *r; } typedef node *link;

ЧТО Представляет собой всего лищь код С++ для определения 5.1. Узлы состоят из элементов и пар указателей на узлы, и указатели на узлы называются также связями. Так, например, мы реализуем абстрактную операцию перехода к левому поддереву с помощью ссылки на указатель типа х = х->1.

Это стандартное представление позволяет построить эффективную реализацию операций, которые вызываются для перемещения по дереву вниз от корня, но не для перемещения по дереву вверх от дочернего узла к его родительскому узлу. Для алгоритмов, требующих использования таких операций, можно добавить третью связь для каждого узла, направленную к его родительскому узлу. Эта альтернатива аналогична двухсвязным спискам. Как и в случае со связными списками (см. рис. 3.6), в определенных ситуациях узлы дерева хранятся в массиве, а в качестве связей используются индексы, а не указатели. Конкретный пример такой реализации исследуется в разделе 12.7. Для определенных специальных алгоритмов используются другие представления бинарных деревьев, что наиболее полно исследуется в главе 9.

Из-за наличия такого множества различных возможных представлений можно было бы разработать ADT (Abstract Data Type) (абстрактный тип данных) бинарного дерева, инкапсулирующий важные операции, которые нужно выполнять, и разделяющий использование и реализацию этих операций. В данной книге данный подход не используется, поскольку

чаще всего мы используем представление с двумя связями;

мы используем деревья для реализации ADT более высокого уровня, и хотим сосредоточить внимание на этой теме;

мы работаем с алгоритмами, эффективность которых зависит от конкретного представления, - это обстоятельство может быть упущено в ADT.

По этим же причинам мы используем уже знакомые конкретные представления массивов и связных списков. Представление бинарного дерева, отображенное на рис. 5.21 - один из фундаментальных инструментов, который теперь добавлен к этому краткому списку.

Анализируя связные списки, мы начали рассмотрение с элементарных операций вставки и удаления узлов (см. рис. 3.3 и 3.4). При использовании стандартного представления бинарных деревьев такие операции необязательно являются элементарными из-за наличия второй связи. Если нужно удалить узел из бинарного дерева, приходится рещать принципиальную проблему наличия двух дочерних узлов и только одного родительского, с которыми нужно работать после удаления узла. Существуют три естественных операции, для которых подобное осложнение не возникает: вставка нового узла в нижней части дерева (замена нулевой связи связью с новым узлом), удаление листа (замена связи с ним нулевой связью) и объединение двух деревьев посредством создания нового корня, левая связь которого указывает на одно дерево, а правая - на другое. Эти операции интенсивно используются при манипулировании бинарными деревьями.