Программа 5.12 - прямое рекурсивное решение, основывающееся на приведенных рассуждениях. Эта программа также неприменима для решения встречающихся на практике задач, поскольку из-за большого объема повторных вычислений (см. рис. 5.17) время решения связано с количеством элементов экспоненциально. Но для решения проблемы можно автоматически задействовать нисходящее динамическое профаммирование, как показано в программе 5.13. Как и ранее, эта методика исключает все повторные вычисления (см. рис. 5.18).

Программа 5.12 Задача о ранце (рекурсивная реализация)

Аналогично тому, как мы предостерегали в отношении рекурсивного решения задачи вычисления чисел Фибоначчи, не следует использовать эту программу, поскольку для ее выполнения потребуется время, экспоненциально связанное с количеством элементов, и поэтому, возможно, даже небольшой задачи решение получить не удастся. Тем не менее, программа представляет компактное решение, которое легко можно усовершенствовать (см. программу 5.13). В ней предполагается, что элементы являются структурами с размером и стоимостью, которые определены следующим образом

typedef struct { int size; int val; } Item;

кроме того, в нашем распоряжении имеется массив N элементов типа Item. Для каждого возможного элемента мы вычисляем (рекурсивно) максимальную стоимость, которую можно было бы получить, включив этот элемент в выборку, а затем выбираем максимальную из всех стоимостей.

int knap(int cap) { int i, space, max, t ; for (i = 0, max = 0; i < N; i++) if ((space = cap-items[i].size) >= 0) if ((t = knap(space) + items [i] .val) > max) max = t ; return max;

РИСУНОК 5.17 РЕКУРСИВНАЯ СТРУКТУРА АЛГОРИТМА РЕЩЕНИЯ ЗАДАЧИ О РАНЦЕ.

Это дерево представляет структуру рекурсивных вызовов простого рекурсивного алгоритма решения задачи о ранце, реализованного в программе 5.12. Число в каждом узле представляет остающееся свободным пространство ранца. Недостатком алгоритма является то же экспоненциальное снижение производительности вследствие большого объема повторных вычислений, требуемых для решения перекрывающихся подзадач, которое рассматривалось при вычислении чисел Фибоначчи (см. рис. 5.14).

Программа 5.13 Задача о ранце (динамическое программирование)

Эта программа, которая представляет собой механически измененную программу 5.12, снижает с экспоненциальной до линейной зависимость времени выполнения от количества элементов. Мы просто сохраняем любые вычисленные значения функции, а затем вместо выполнения рекурсивных вызовов получаем любые сохраненные значения, когда они требуются (используя зарезервированное значение для представления неизвестных значений). Индекс элемента сохраняется, поэтому при жепаьт всегда можно восстановить содержимое ранца после вычисления: itemKnown[M] находится в ранце, остальное содержимое совпадает с оптимальной упаковкой ранца размера M-itemKnown[M].size, следовательно, iteniKnown[M-items[M].size] находится в ранце и т.д.

int knap(int М) { int i, space, tnax, maxi = 0, t; if (maxKnown[M] != unknown) return maxKnown[M]; for (i = 0, max = 0; i < N; i++) if ((space = M-items[i] .size) >= 0) if ((t = knap(space) + items [i] .val) >max) { max = t; maxi = i; } maxKnown[M] = max; itemKnown[M] = items [maxi] ; return max;

Динамическое программирование принципиально исключает все повторные вычисления в любой рекурсивной профамме, при условии, что мы можем себе позволить сохранять значения функции для аргументов, которые меньше чем интересующий вызов.

Лемма 5.3 Динамическое программирование уменьшает время выполнения рекурсивной функции до максимального значения, которое потребуется на вычисление функции для всех аргументов, которые меньше или равны данному аргументу, при условии, что стоимость рекурсивного вызова остается постоянной.

См. упражнение 5.50.

Применительно к задаче о ранце из леммы следует, что время выполнения пропорционально произведению NM. Таким образом, задача о ранце легко поддается решению, когда емкость ранца не очень велика; для очень больших емкостей время и требуемый объем памяти могут оказаться недопустимо большими.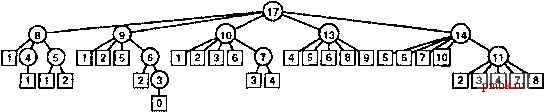

РИСУНОК 5.18 ПРИМЕНЕНИЕ МЕТОДА НИСХОДЯЩЕГО ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ ДЛЯ РЕАЛИЗАЦИИ АЛГОРИТМА РЕШЕНИЯ ЗАДАЧИ О РАНЦЕ

Подобно тому, как это было сделано для вычисления чисел Фибоначчи, методика с сохранением известных значений уменьшает нарастание затрат времени на выполнение алгоритма с экспоненциального (см. рис. 5.17) до линейного.

Восходящее динамическое программирование также применимо к задаче о ранце. Действительно, метод восходящего программирования можно применять во всех случаях, когда применим метод нисходящего программирования, хотя при этом необходимо убедиться, что значения функции могут быть вычислены в соответствующем порядке, чтобы каждое нужное значение вычислялось в требуемый момент. Для функций, имеющих только один целочисленный аргумент, подобных рассмотренным, можно просто увеличить порядок аргумента (см. упражнение 5.53); для более сложных рекурсивных функций определение правильного порядка может быть сложной задачей.

Например, мы не обязаны ограничиваться рекурсивными функциями только с одним целочисленным аргументом. При наличии функции с несколькими целочисленными аргументами рещения меньших подзадач можно сохранить в многомерных массивах, по одному для каждого аргумента. В других ситуациях целочисленные аргументы вообще не требуются, а вместо этого можно использовать абстрактную формулировку отдельной задачи, позволяющую разделить задачу на менее сложные. Примеры таких задач рассмотрены в частях 5-8.

При использовании нисходящего динамического программирования известные значения сохраняются; при использовании восходящего динамического программирования они вычисляются заранее. В общем случае нисходящее динамическое программирование предпочтительней восходящего, поскольку

оно представляет собой механическую трансформацию естественного решения задачи;

порядок решения подзадач определяется сам собой;

решение всех подзадач может не потребоваться.

Приложения, в которых применяется динамическое программирование, различаются по сущности подзадач и объему сохраняемой для них информации.

Важный момент, которым нельзя пренебрегать, заключается в том, что динамическое программирование становится неэффективным, когда количество возможных значений функции, которые могут потребоваться, столь велико, что мы не можем себе позволить их сохранять (при нисходящем программировании) или вычислять предварительно (при восходящем программировании). Например, если в задаче о ранце М и размеры элементов - 64-разрядные величины или числа с плавающей точкой, мы не сможем сохранять значения путем их индексирования в массиве. Это несоответствие - не просто небольшое неудобство - оно создает принципиальные трудности. Для подобных задач пока не известно ни одного достаточно эффективного решения; как будет показано в части 8, имеются веские причины считать, что эффективного решения вообще не существует.

Динамическое программирование - это методика разработка алгоритмов, которая рассчитана в первую очередь для решения сложных задач того типа, который будет рассмотрен в частях 5-8. Большинство рассмотренных в частях со 2 по 4 алгоритмов представляют собой реализацию методов типа разделяй и властвуй с неперекрывающимися подзадачами, и основное внимание было уделено скорее субквадратичной или сублинейной зависимости производительности, чем субэкспоненциальной. Однако, нисходящее динамическое программирование является базовой