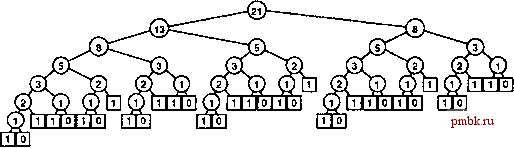РИСУНОК 5.14 СТРУКТУРА РЕКУРСИВНОГО АЛГОРИТМА ДЛЯ ВЫЧИСЛЕНИЯ ЧИСЕЛ ФИБОНАЧЧИ

Схема рекурсивных вызовов для вычисления Г по стандартному рекурсивному алгоритму иллюстрирует, как рекурсия с перекрывающимися подзадачами может приводить к экспоненциальному возрастанию затрат. В данном случае второй рекурсивный вызов игнорирует вычисление, выполненное во время первого вызова, что приводит к значительным повторным вычислениям, поскольку эффект нарастает в геометрической прогрессии с увеличением количества рекурсивных вызовов. Рекурсивные вызовы для вычисления Г= 8 (отраженные в правом поддереве корня и в левом поддереве левого поддерева корня) показаны ниже.

8F(6) б F(5) 3F(4) 2F(3) 1F(2) 1F(1) 0F(0) 1F(1) 1F(2) 1F(1) 0F(0)

2F(3) 1FC2) 1F(1) 0F(0) IFCl) 3F(4) 2 F(3) 1 F(2) IFCl) 0F(0) 1 F(l) 1 F(2) IFCl) OF(O)

Программа 5.10 Числа фибоначчи (рекурсивная реализация)

Эта программа, хотя она выглядит компактно и изящно, неприменима на практике, поскольку время вычисления Рц экспоненциально зависит от N. Время вычисления F+i в 0 = 1,6 раз больше времени вычисления Рц. Например, поскольку 0 > 60, если для вычисления Fn компьютеру требуется около секунды, то для вычисления F+g потребуется более минуты, а для вычисления - более часа.

int F(int i) {

if (i < 1) return o; if (i == 1) return 1; return F(i-l) + F(i-2);

Числа возрастают экспоненциально, поэтому размер массива невелик - например, f45 = 1836311903 - наибольщее число Фибоначчи, которое может быть представлено 32-разрядным целым, поэтому достаточно использовать массив с 46 элементами.

Этот подход предоставляет непосредственный способ получения численных решений для любых рекуррентных соотношений. В случае с числами Фибоначчи можно даже обойтись без массива и ограничиться только первыми двумя значениями (см. упражнение 5.37); для многих других часто встречающихся рекуррентных соотношений (см., например, упражнение 5.40) необходимо поддерживать массив, хранящий все известные значения.

Рекуррентное соотношение - это рекурсивная функция с целочисленными значениями. Рассуждения, приведенные в предьщущем абзаце, подсказывают, что любую такую функцию можно приближенно вычислить, вычисляя все значения функции, начиная с наименьшего, используя на каждом шаге ранее вычисленные значения для подсчета текущего значения. Эта технология называется восходящим динамическим про-

граммированием (battom-up dynamic programming). Она применима к любому рекурсивному вычислению при условии, что мы можем себе позволить хранить все ранее вычисленные значения. Такая технология разработки алгоритмов успешно используется для решения широкого круга задач. Поэтому следует уделить внимание простой технологии, которая может изменить зависимость времени выполнения алгоритма от значения аргументов с экспоненциальной на линейную!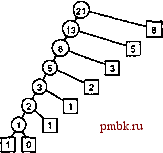

РИСУНОК 5.15 ПРИМЕНЕНИЕ НИСХОДЯЩЕГО ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ ДЛЯ ВЫЧИСЛЕНИЯ ЧИСЕЛ ФИБОНАЧЧИ

Из этой схемы рекурсивных вызовов, использованных для

вычисления методом нисходящего динамического программирования, видно, как сохранение вычисленных значений снижает нарастание затрат с экспоненциального (см. рис. 5.14) до линейного.

Нисходящее динамическое программирование (top-down dynamic programming) - еше более простая технология, которая позволяет автоматически выполнять рекурсивные функции при том же (или меньшем) количестве итераций, что и восходящее динамическое программирование. При этом рекурсивная программа используется для сохранения каждого вычисленного ею (в качестве заключительного действия) значения и для проверки сохраненных значений во избежание повторного вычисления любого из них (в качестве первого действия). Программа 5.11 - механически измененная программа 5.10, в которой за счет применения нисходящего динамического программирования достигается снижение времени выполнения - его зависимость от размера входного массива становится линейной. Рисунок 5.15 служит иллюстрацией радикального

уменьшения количества рекурсивных вызовов, достигнутого посредством этого простого автоматического изменения. Иногда нисходящее динамическое программирование называют также мемуаризацией (memoization).

Программа 5.11 Числа Фибоначчи (динамическое программирование)

Сохранение вычисляемых значений в статическом массиве (элементы которого в С++ инициализируются 0) явным образом исключает любые повторные вычисления. Эта программа вычисляет Рц за время, пропорциональное N, что разительно отличается от времени 0(ф), которое требуется для вычисления в программе 5.10.

int F(int i)

{ static int knownF [niaxN] ; if (lcnownF[i] 1= 0) return knownF[i] ; int t = i;

if (i < 0) return 0;

if (i > 1) t = F(i-l) + F(i-2);

return lcnownF[i] = t;

В качестве более сложного примера давайте рассмотрим задачу о ранце: вор, грабящий сейф, находит в нем видов предметов различных размеров и ценности, но имеет только небольшой ранец емкостью М, в котором может унести награбленное. Задача заключается в том, чтобы определить комбинацию предметов, которые вор должен уложить в ранец, чтобы общая стоимость похищенного оказалась наиболь-

шей. Например, при наличии типов предметов, представленных на рис. 5.16, вор, располагающий ранцем, размер которого равен 17, может взять только пять (но не шесть) предметов А общей стоимостью равной 20 или предметы D и Е суммарной стоимостью равной 24 или предметы в одной из множества других комбинаций. Наша цель - найти эффективный алгоритм для определения максимума среди всех возможностей при любом заданном наборе предметов и вместимости ранца.

Решения задачи о ранце важны во многих приложениях. Например, транспортной компании может требоваться определение наилучшего способа загрузки грузовика или транспортного самолета. В подобных приложениях могут встречаться и другие варианты этой задачи: например, количество элементов каждого вида может быть ограничено или могут быть доступны два грузовика. Многие из таких вариантов могут решаться путем применения того же подхода, который мы собираемся исследовать для решения только что сформулированной базовой задачи; другие варианты оказываются гораздо более сложными. Можно четко разграничить решаемые и нерешаемые задачи этого типа, что исследуется в части 8.

В рекурсивном решении задачи о ранце при каждом выборе предмета мы предполагаем, что можем (рекурсивно) определить оптимальный способ заполнения остающегося пространства в ранце. Для ранца размера cap, для каждого доступного типа элемента i определяется общая стоимость элементов, которые можно было бы унести, укладывая 1-ый элемент в ранец при оптимальной упаковке остальных элементов. Этот оптимальный способ упаковки - просто способ упаковки, определенный (или который будет определен) для меньшего ранца размера cap-items[i].size. В этом решении используется следующий принцип: оптимальные принятые решения в дальнейшем не требуют пересмотра. Как только установлено, как оптимально упаковать ранцы меньших размеров, эти задачи не требуют повторного исследования независимо от следующих элементов.

предмеФ

размер

ценность

2 3 4

С D Е

7 8 9

10 11 13

А В

А с с

г-г-Г

ААВ С

I I I

АААВ в

РИСУНОК 5.16 ПРИМЕР ЗАДАЧИ О РАНЦЕ

Входными данными примера задачи о ранце (вверху) являются емкость ранца и набор предметов различных размеров (которые представлены значениями на горизонтальной оси) и стоимости (значения на вертикальной оси). На этом рисунке показаны четыре различных способа заполнения ранца, размер которого равен 17; два из этих способов ведут к получению максимальной суммарной стоимости, равной 24.