той же причине, что каждое второе число является нечетным, а каждая вторая метка на линейке является самой короткой. Вероятно, наши монах знали этот секрет, поскольку трудно себе представить, как иначе они могли бы определить нужные перемещения.

Формальное доказательство методом индукции того, что в решении задачи о ханойских башнях каждое второе перемещение затрагивает маленький диск (все начинается и завершается такими перемещениями), весьма поучительно: Для п = 1 существует только одно перемещение, затрагивающее маленький диск, следовательно, утверждение подтверждается. При л > 1 из предположения, что утверждение справедливо для п-1, следует его справедливость и для п. Это можно подтвердить, прибегнув к следующей рекурсивной конструкции: первое решение для п - 1 начинается с перемещения маленького диска, а второе решение для п ~ 1 завершается перемещением маленького диска, следовательно, решение для п начинается и завершается перемещением маленького диска. Мы поместили перемещение, не затрагивающее маленький диск, между двумя перемещениями, которые его затрагивают (перемещением, завершающим первое решение для л - 1, и перемещением, начинающим второе решение для п- 1), следовательно, утверждение, что каждое второе перемещение затрагивает маленький диск, подтверждается.

Программа 5.9 представляет альтернативный способ рисования линейки, на который натолкнуло соответствие с двоичными числами (см. рис. 5.10). Эту версию алгоритма называют восходящей (bottom-up) реализацией. Она не является рекурсивной, но определенно навеяна рекурсивным алгоритмом. Это соответствие между алгоритмами типа разделяй и властвуй и двоичными представлениями чисел часто способствует углубленному пониманию при анализе и разработке усовершенствованных версий, таких как восходящие подходы. Данную возможность следует учитывать, чтобы понять и, возможно, усовершенствовать каждый из исследуемых алгоритмов типа разделяй и властвуй .

Программа 5.9 Не рекурсивная программа для рисования линейки

в противоположность программе 5.8, линейку можно нарисовать, вначале изобразив все метки длиной 1, затем все метки длиной 2 и т.д. Переменная t представляет длину меток, а переменная j - количество меток между двумя последовательными метками длиной t. Внешний цикл for увеличивает значение t при сохранении соотношения j=2* Внутренний цикл for рисует все метки длиной t.

void rule (int 1, int r, int h)

for (int t = 1, j = 1;

t <= h; j += j, t++) for (int i = 0; 1+j+i <= r; i += j+j)

mark(1+j+i, t);

РИСУНОК 5.10 РИСОВАНИЕ ЛИНЕЙКИ В ВОСХОДЯЩЕМ ПОРЯДКЕ

Для рисования линейки не рекурсивным методом вначале рисуются все метки длиной I и пропускаются позиции, затем рисуются метки длиной 2 и пропускаются остающиеся позиции, затем рисуются метки длиной 3 с пропуском остающихся позиций и т.д.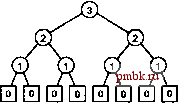

Восходящий подход предполагает изменение порядка выполнения вычислений при рисовании линейки. На рис. 5.11 показан еще один пример, в котором порядок следования трех вызовов функций в рекурсивной реализации изменяется. Этот пример отражает выполнение рекурсивного вычисления первоначально описанным способом: рисование средней метки, затем рисование левой половины, а затем правой. Последовательность рисования меток сложна, но является результатом простой перемены мест двух операторов в профамме 5.8. Как будет показано в разделе 5.6, взаимосвязь между рис. 5.8 и 5.11 сродни различию между постфиксными и префиксными арифметическими выражениями.

Рисование меток в порядке, показанном на рис. 5.8, может оказаться более предпочтительным по сравнению с выполнением вычислений в измененном порядке, содержащихся в программе 5.9 и приведенных на рис. 5.11, поскольку можно нарисовать линейку произвольной длины. Достаточно представить себе графическое устройство, которое просто перемещается вдоль непрерывной ленты к следующей метке. Аналогично, при решении задачи о ханойских башнях мы ограничиваемся перемещением дисков в требуемом порядке перемещения. Вообще говоря, многие рекурсивные программы основываются на решениях подзадач, которые должны быть выполнены в конкретном порядке. Для других вычислений (например, см. программу 5.6) порядок решения подзадач роли не играет. Для таких вычислений единственным Офаничением служит необходимость решения подзадач перед тем, как можно будет решить главную задачу. Понимание того, когда можно изменять порядок вычисления, не только служит ключом к успешной разработке алгоритма, но и оказывает непосредственное практическое влияние во многих случаях. Например, этот вопрос исключительно важен при исследовании возможности реализации алгоритмов в параллельных процессорах.

Восходящий подход соответствует общему методу разработки алгоритмов, при котором задача решается путем решения вначале элементарных подзадач с последующим объединением этих решений для получения решения несколько больших подзадач и т.д., пока вся задача не будет решена. Подобный подход можно было бы назвать подходом объединяй и властвуй .

mle(0, 8, 3) mark(4, 3) ruleCO, 4, 2) mark(2, 2) rule (О, 2, 1) markCl, 1) ruleCO, 1, 0) rule CI. 2, 0) rule(2, 4, 1) тагкСЗ, 1) rule(2, 3, 0) ruleC3, 4, 0) rule(4, 8, 2) mark(6, 2) rule (4, 6, 1) mark(5, 1) rule(4, 5, 0) rule(5, 6, 0) rule(6. 8, 1) mark(7, 1) rule (6, 7, 0) rule(7, 8, 0)

РИСУНОК 5.11 ВЫЗОВЫ ФУНКЦИЙ для РИСОВАНИЯ ЛИНЕЙКИ (ВЕРСИЯ С ИСПОЛЬЗОВАНИЕМ ПРЯМОГО ОБХОДА)

Эта последовательность отображает результат рисования меток перед рекурсивными вызовами, а не между ними.

(5 < + . -

i4 .

Лишь небольшой шаг отделяет рисование линеек от рисования двумерных узоров, похожих на показанный на рис. 5.12. Этот рисунок иллюстрирует, как простое рекурсивное описание может приводить к сложным вычислениям (см. упражнение 5.30).

Рекурсивно определенные геометрические узоры, наподобие показанного на рис. 5.12, иногда называют фракталами. При использовании более сложных примитивов рисования и более сложных рекурсивных функций (особенно, включая рекурсивно определенные функции, работающие как с действительными значениями, так и в комплексной плоскости), можно разрабатывать поразительно разнообразные и сложные узоры. На рис. 5.13 приведен еще один пример - звезда Коха, которая определяется рекурсивно следующим образом: звезда Коха О порядка - простой выступ, показанный на рис. 4.3, а звезда Коха п порядка - это звезда Коха порядка л - 1, в которой каждый линейный сегмент заменен соответствующим образом отмасштабированной звездой О порядка.

Подобно решениям задач рисования линейки и ханойских башен, эти алгоритмы линейны по отношению к количеству шагов, но это количество связано экспоненциальной зависимостью с максимальной глубиной рекурсии (см. упражнения 5.29 и 5.33). Кроме того, они могут быть непосредственно связаны с подсчетом в соответствующей системе счисления (см. упражнение 5.34).

Задача о ханойских башнях, рисование линейки и фракталы весьма занимательны, а связь с двоичным числами поражает, однако все эти вопросы интересуют нас прежде всего потому, что облегчают понимание одного из основных методов разработки алгоритмов - деление задачи пополам и независимое решение одной или обеих половин задачи; возможно, это - наиболее важная из подобного рода технологий, рассматриваемых в книге. В табл. 5.1 подробно описаны бинарный поиск и сортировка слиянием, которые не только являются важными и широко используемыми на практике алгоритмами, но и служат типичными примерами разработки алгоритмов типа разделяй и властвуй .

Таблица 5.1 Основные алгоритмы типа

разделяй и влаавуй

Бинарный поиск (см. главы 2 и 12) и сортировка слиянием (см. главу 8) - прототипы алгоритмов типа разделяй и властвуй , которые обеспечивают гарантированную оптимальную производительность, соответственно, поиска и сортировки. Рекуррентное соотношение демонстрирует сущность вычислений методом разделяй и властвуй для

йшййШй

РИСУНОК 5.12 ДВУМЕРНАЯ ФРАКТАЛЬНАЯ ЗВЕЗДА

Этот фрактал - двумерная версия рис. 5.10. Очерненные квадраты на нижнем рисунке подчеркивают рекурсивную структуру вычисления.