6 10

Программа 5.6 - типичный пример для многих алгоритмов типа разделяй и властвуй , имеющих совершенно одинаковую рекурсивную структуру, но другие примеры могут отличаться от приведенного в двух аспектах. Во-первых, программа 5.6 выполняет одинаковый объем вычислений для каждого вызова функции, и поэтому ее общее время выполнения линейно связано с количеством вызовов. Как будет показано, другие алгоритмы типа разделяй и властвуй могут выполнять различный объем вычислений для различных вызовов функций, и поэтому для определения общего времени выполнения требуется более сложный анализ. Время выполнения таких алгоритмов зависит от конкретного способа разделения на части. Во-вторых, программа 5.6 - типичный пример алгоритмов типа разделяй и властвуй , для которых сумма размеров частей равна общей размерности. Другие алгоритмы типа разделяй и властвуй могут разделять задачу на части, сумма размеров которых меньше или больше размерности всей задачи. Эти алгоритмы все же относятся к рекурсивным алгоритмам типа разделяй и властвуй , поскольку каждая часть меньше целого, но анализировать их труднее, нежели программу 5.6. Мы подробно рассмотрим процесс анализа таких типов алгоритмов, как только столкнемся с ними.

Например, алгоритм бинарного поиска, приведенный в разделе 2.6, является алгоритмом типа разделяй и властвуй , который делит задачу пополам, а затем работает только с одной из этих половин. Рекурсивная реализация бинарного поиска исследуется в главе 12.

На рис. 5.5 показано содержимое внутреннего стека, поддерживаемого средой программирования для реализации вычислений, изображенных на рис. 5.4. Приведенная на рисунке модель является идеализированной, но она позволяет взглянуть на структуру вычисления по методу разделяй и властвуй изнутри. Если программа имеет два рекурсивных вызова, фактический внутренний стек содержит одну запись, соответствующую первому вызову функции во время выполнения (эта запись содержит значения аргументов, локальные переменные и адрес возврата), и аналогичную запись, соответствующую второму вызову функции во время ее выполнения. Альтернатива продемонстрированному на рис. 5.5 подходу - помещение в стек сразу двух значений с сохранением всех подстеков, которые должны явно создаваться в стеке. Такая организация проясняет структуру вычислений и закладывает основу

РИСУНОК 5.5 ПРИМЕР ДИНАМИКИ ВНУТРЕННЕГО СТЕКА

Эта последовательность - идеализированное представление содержимого внутреннего стека во время вычисления примера из рис. 5.4. Обработка начинается с левого и правого индексов всего подмассива в стеке. Каждая строка представляет результат помещения в стек двух индексов и, если они не равны, проталкивания четырех индексов, которые ограничивают левый и правый подмасивы после разделения помещенного подмассива на две части. На практике вместо выполнения упомянутых действий система хранит в стеке адреса возврата и локальные переменные, тем не менее, приведенная модель вполне адекватно описывает вычисление.

для более общих вычислительных схем, подобных исследуемым в разделах 5.6 и 5.8.

На рис. 5.6 показана структура алгоритма разделяй и властвуй для поиска максимального значения. Эта структура является рекурсивной: верхний узел содержит размер входного массива; структура левого подмассива изображена слева, а правого - справа. Формальное определение и описание структур деревьев такого типа можно найти в разделах 5.4 и 5.5. Они облегчают понимание структуры любых программ, в которых используются вложенные вызовы функций - в частности, рекурсивных программ. На рис. 5.6 показано также это же дерево, но с узлами, помеченными возвращаемым значением из соответствующего обращения к функции. Процесс создания явно связанных структур, которые представляют деревья, подобные этому, рассматривается в разделе 5.7.

Ни одно рассмотрение рекурсии не было бы полным без рассмотрения старинной задачи о ханойских башнях. Имеется три стержня и N дисков, которые помещаются на трех стержнях. Диски различаются размерами и вначале размещаются на одном из стержней от самого большого (диск ЛО внизу до самого маленького (диск 1) вверху. Задача состоит в перемещении дисков на соседнюю позицию (стержень) при соблюдении следующих правил: (i) одновременно можно перемещать только один диск; и (ii) ни один диск не может быть помещен поверх диска меньшего размера. Легенда гласит, что конец света наступит раньше, чем группа монахов справится с задачей размещения 40 золотых дисков на трех алмазных стержнях.

Программа 5.7 предоставляет рекурсивное решение этой задачи. Программа указывает диск, который должен бьггь сдвинут на каждом шагу, и направление его перемещения (+ означает перемещение на один стержень вправо с переходом к крайнему слева стержню при достижении крайнего справа стержня, а - означает перемещение на один стержень влево с переходом к крайнему справа стержню при достижении крайнего слева стержня). Рекурсия основывается на следующей идее: для перемещения N дисков вправо на один стержень вначале верхние Л - 1 дисков нужно переместить на один стержень влево, затем переместить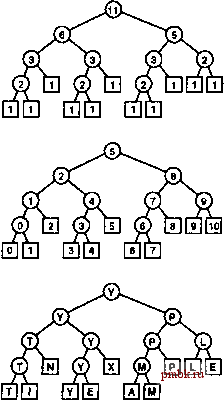

РИСУНОК 5.6 РЕКУРСИВНАЯ СТРУКТУРА АЛГОРИТМА ПОИСКА МАКСИМУМА.

Алгоритм разделяй и властвуй разделяет представляющий задачу массив, размер которого равен 11, на массивы с размерами 6 и 5, массив с размером 6 - на два массива с размерами 3 и т.д., пока не будет получен массив с размером 1 (верхний). Каждая окружность на этих схемах представляет вызов рекурсивной функции для расположенных непосредственно под ней узлов, связанных с ней линиями (квадраты представляют вызовы, для которых рекурсия завершается). На схеме в центре показано значение индекса в середине файла, который использовался для выполнения разделения; на нижней схеме показано возвращаемое значение.

диск N на один стержень вправо, после чего еше раз переместить 7V - 1 дисков на один стержень влево (поверх диска Л. В правильности работы этого решения можно удостовериться методом индукции. На рис. 5.7 показаны перемещения для N - 5 и рекурсивные вызовы для = 3. Структура алгоритма достаточно очевидна; давайте рассмотрим его подробно.

Программа 5.7 Решение задачи о ханойских башнях

Мы сдвигаем башню из дисков вправо, сдвигая (рекурсивно) все диски, кроме нижнего, влево, затем сдвигаем нижний диск вправо, после чего перемещаем (рекурсивно) башню поверх нижнего диска.

void hanoi(int N, int d) {

if (N = 0) return; hanoi(N-l, -d) ; shift(N, d) ; hanoi(N-1, -d) ;

Во-первых, рекурсивная структура этого решения немедленно диктует количество необходимых перемещений.

Лемма 5.2 Рекурсивный алгоритм разделяй и властвуй решения задачи о ханойских башнях дает решение, приводящее к 2 - \ перемещениям.

Как обычно, из кода немедленно следует, что количество перемещений удовлетворяет условию рекуррентности. В данном случае количество перемещений дисков, удовлетворяющее условию рекуррентности, определяется формулой, аналогичной формуле 2.5:

Tn = 2Tn~i + \, при N>2,T, = \.

Предсказанный результат можно непосредственно проверить методом индукнии: мы имеем Г(1) = 2 - 1 = 1; и, если Т(к) = 2* - 1 для к < N, то T{N) = 2(2-- 1) + 1= 2- 1.

Если монахи перемещают по одному диску в секунду, для заверщения работы им потребуется, по меньшей мере, 348 столетий (см. рис. 2.1), разумеется, если они не допускают ошибок. Скорее всего, конец света может наступить даже позже этого срока, поскольку монахи никак не смогли бы воспользоваться программой 5.7 для быстрого выяснения, какой диск нужно перемещать следующим. А теперь давайте проанализируем метод, который ведет к простому (не рекурсивному) решению, упрощающему принятие решения. Хоть и не хочется оставлять бедных монахов в неведении, однако этот метод имеет большое значение для множества важных применяемых на практике алгоритмов.

Чтобы понять решение задачи о ханойских башнях, давайте рассмотрим простую задачу рисования меток на линейке. Каждые 1/2 дюйма на линейке отмечаются черточкой, каждые 1/4 дюйма отмечаются несколько более короткими черточками, 1/8 дюйма - еще более короткими и т.д. Задача состоит в создании программы для рисования этих меток при любом заданном разрешении, при условии, что в нашем распоряжении имеется процедура mark(x, h) для рисования меток высотой h условных единиц в позиции х.