Предположим, что граф с количеством вершин V и количеством ребер Е описывается набором из Е пар целых чисел в диапазоне от О до V-1. Это означает, что вершины обозначены целыми числами О, 1, V-1, а ребра определяются парами вершин. Как и в главе 1, пара i-j обозначает связь между вершинами i и j, и имеет то же значение, что и пара j-i. Составленные из таких ребер графы называются неориентированными (undirected). Другие типы графов рассматриваются в части 7.

Один из простых методов представления графа заключается в использовании двумерного массива, называемого матрицей смежности (adjacency matrix). Она позволяет быстро определять, существует ли ребро между вершинами i и j путем простой проверки наличия ненулевого значения в записи матрицы, находящейся на пересечении строки i и столбца j. Для неориентированных графов, к которым принадлежит рассматриваемый, при наличии записи в строке i и столбце j обязательно существует запись в строке j и столбце i. Поэтому матрица симметрична. На рис. 3.14 показан пример матрицы смежности для неориентированного графа. Программа 3.18 демонстрирует создание матрицы смежности для вводимой последовательности ребер.

Программа 3.18 Предаавление графа в виде матрицы смежности

Эта программа выполняет чтение набора ребер, описывающих неориентированный граф, и создает для него представление в виде матрицы смежности. При этом элементам a[i][j] и a[j][l] присваивается значение 1, если существует ребро от i до j либо от j до i. В противном случае элементам присваивается значение 0. В программе предполагается, что во время компиляции количество вершин V постоянно. Иначе пришлось бы динамически выделять память под массив, представляющий матрицу смежности (см. упражнение 3.71).

#include <iostreeun.h> int main О { int i , j , adj [V] [V] ; for (i = 0; i < V; i++) for (j = 0; j < V; j++) adj[i] [j] = 0; for (i = 0; i < V; i++) adj[i][i] = 1; while (cin i j)

{ adj[i][j] = 1; adj[j][i] = 1; }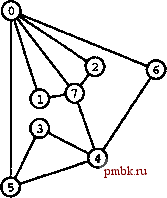

0 1 2 3 4 5 6 7

01234567

1 1 1 0 0

1 1 1

0 0 0 0 0

0 0 0

0 0 0

1 1 1

0 0 0

1 1 1 1 1

0 0 0

0 0 0

0 0 0 0

РИСУНОК 3.14 ПРЕДСТАВЛЕНИЕ ГРАФА В ВИДЕ МАТРИЦЫ СМЕЖНОСТИ

Граф представляет собой набор вершин и ребер, которые их соединяют. Для простоты вершинам присваиваются индексы (последовательность неотрицательных целых чисел, начиная с нуля). Матрица смежности - это двумерный массив, где граф представляется за счет установки разряда (значения 1) в строке i и столбце j в том и только том случае, когда между вершинами i и j существует ребро. Массив симметричен относительно диагонали. По соглашению разряды устанавливаются во всех позициях диагонали (каждая вершина соединена сама с собой). Например, шестая строка (и шестой столбец) показывают, что вершина б соединена с вершинами О, 4 и 6.

Другой простой метод представления графа предусматривает использование массива связанных списков, называемых списками смежности (adjacency lists). Каждой вершине соответствует связный список с узлами ддя всех вершин, связанных с данной, В неориентированных графах, если существует узел для вершины j в i-том списке, то должен существовать узел для вершины i в j-том списке. На рис. 3.15 показан пример представления неориентированного графа с помощью списков смежности. Программа 3.19 демонстрирует метод создания такого представления для вводимой последовательности ребер.

Программа 3.19 Представление графа в виде списков смежности

Эта программа считывает набор ребер, которые описывают граф, и создает его представление в виде списков смежности. Список смежности представляет собой массив списков, по одному для каждой вершины, где j-тый список содержит связный список узлов, присоединенных к j-той вершине.

finclude <iostream.h> struct node { int v; node* next; node(int X, node* t) { V = x; next = t; }

typedef node *lin]c; int mainO { int i, j; link adj[V] ; for (i = 0; i < V; i++) adj[i] while (cin i j) {

adjlj] = new node(i, adj[j]); adj[i] = new node(j, adj [i]) ;

РИСУНОК 3.15 ПРЕДСТАВЛЕНИЕ ГРАФА В ВИДЕ СПИСКОВ СМЕЖНОСТИ

В этом представлении графа, изображенного на рис. 3.14, применен массив списков. Необходимое для данных пространство пропорционально сумме количеств вершин и ребер. Для поиска индексов вершин, присоединенных к данной вершине i, анализируется i-тая позиция массива, содержащая указатель связного списка, который содержит по одному узлу для каждой присоединенной к i вершины.

Оба представления фафа являются массивами более простых структур данных (по одной для каждой вершины), которые описывают ребра, связанные с данной вершиной. Для матрицы смежности более простая структура данных реализована в виде индексированного массива, а для списка смежности - в виде связного списка.

Таким образом, представление графа различными методами создает альтернативные возможности расхода пространства. Для матрицы смежности необходимо пространство, пропорциональное V; для списков смежности расход памяти пропорционален величине V + Е. При небольшом количестве ребер (такой граф называется разреженным), представление/: использованием списков смежности потребует намного меньшего размера пространства. Если большинство пар вершин соединены ребрами (такой фаф называется насыщенным), использование матрицы смежности предпочтительнее, поскольку оно не связано со ссылками. Некоторые алгоритмы более эффективны для представлений на базе матрицы смежности, поскольку требуют постоянных затрат времени для ответа на вопрос: существует ли ребро между вершинами i и j? . Другие алгоритмы более эффективны для представлений на базе списков смежности, поскольку они позволяют обрабатывать все ребра графа за время, пропорциональное V + Е, а не V. Показательный пример этой альтернативы продемонстрирован в разделе 5.8.

Оба типа представлений можно элементарно распространить на другие типы графов (для примера см. упражнение 3.70). Они служат основой большинства алгоритмов обработки графов, которые будут исследоваться в части 7.

В завершение главы рассмотрим пример, демонстрирующий использование составных структур данных для эффективного решения простой геометрической задачи, о которой шла речь в разделе 3.2. Для данного значения d необходимо узнать количество пар из множества N точек внутри единичного квадрата, которые можно соединить отрезком прямой с длиной меньшей d. Программа 3.20 призвана снизить время выполнения профаммы 3.8 с приблизительным коэффициентом 1/d при больших значениях N. Для этого в программе задействован двумерный массив связных списков. Единичный квадрат разбивается на сетку меньших квадратов одинакового размера. Затем для каждого квадрата создается связный список всех точек, попадающих в квадрат. Двумерный массив обеспечивает немедленный доступ к набору точек, который является ближайшим по отношению к данной точке. Связные списки обладают гибкостью, позволяющей хранить все точки без необходимости знать заранее, сколько точек попадает в каждую ячейку сетки.

Используемое программой 3.20 просфанство пропорционально 1/d + N, но время выполнения составляет 0(dW), что дает большое преимущество перед прямолинейным алгоритмом из программы 3.8 при небольших значениях d. Например, для N = 10 и d = 0.001 зафаты времени и пространства на решение задачи будут практически линейно зависеть от N. При этом прямолинейный алгоритм потребует неоправданно высоких затрат времени. Эту структуру данных можно использовать в качестве основы для решения многих других геомефических задач. Например, совместно с алгоритмом union-find из главы 1 это даст близкий к линейному алгоритм определения факта возможности соединения отрезками длиной d набора из N случайных точек на плоскости. Это фундаментальная задача из области проектирования сетей и цепей.