Выполнение вставок требует всего лишь добавления элемента в страницу, но на основании структуры результирующего дерева можно определить важные события, происходящие во время его построения. Дерево содержит семь внешних страниц, поэтому должно было быть выполнено шесть разделений внешних узлов, и поскольку его высота равна 3, корень дерева должен был разделяться дважды. Эти события описаны в сопровождающих рисунки комментариях.

В программе 16.1 приведены определения типа для узлов рассматриваемой реализации В-дерева. Мы не указываем подробно структуру узлов, что следовало бы сделать в реальной реализации, поскольку для этого потребовалась бы ссылка на конкретные страницы диска. Для простоты мы используем один тип узлов, когда каждый узел состоит из массива записей, каждая из которых содержит элемент, ключ и связь. Каждый узел содержит также счетчик, указывающий количество активных записей. Мы не обращаемся к элементам во внутренних узлах, мы не обращаемся к связям во внешних узлах, и мы не обращаемся к ключам внутри элементов дерева. При использовании конкретной структуры данных в реальном приложении можно сэкономить память за счет применения таких конструкций, как union (объединение) или производные классы. Можно было бы также сэкономить память ценой увеличения времени выполнения, используя везде в дереве связи с элементами вместо ключей. Такие конструктивные решения сопряжены с очевидными изменениями кода и зависят от конкретного характера ключей, элементов и связей в приложении.

153 I 176 I 373 I 513H 524 I

601 706

153 : 17 6 275.

373:

524?

SOli 706 742 ; 766 ; 773

153:

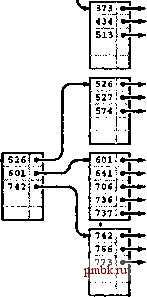
373 513 524

601 706 737

742 766 773

РИСУНОК 16.6 ПОСТРОЕНИЕ В-ДЕРЕВА, ЧАСТЬ 2

После вставки четырех ключей 742, 373, 524 и 766 в крайнее справа В-дерево, показанное на рис. 16.5, обе внешние страницы оказываются заполненными (рисунок слева). Затем, при вставке ключа 275 первая страница разделяется с пересылкой связи с новой страницей (вместе с наименыиим ее ключом 373) вверх в индексе (рисунок в центре). Далее, при вставке ключа 737разделяется нижняя страница, также с пересылкой связи с новой страницей вверх в индексе (рисунок справа).

Программа 16.1 Определения типов узлов В-дерева

Каждый узел в В-дереве содержит массив и счетчик количества активных записей в массиве. Каждая запись массива представляет собой ключ, элемент и связь с узлом. Во внутренних узлах используются только ключи и связи; во внешних узлах используются только ключи и элементы. Новые узлы инициализируются в виде пустых узлов путем установки значения поля счетчика равным 0.

tenlate <class Item, class Кву> struct entry

{ Key key; Item item; struct node *next; }; struct node

{ int m; entry<Item, Key> b[M] ; nodeO { m = 0; }

typedef node *link;

2071

17 6 т-*

60l< 742.

>W 373

513 It

ООО?: -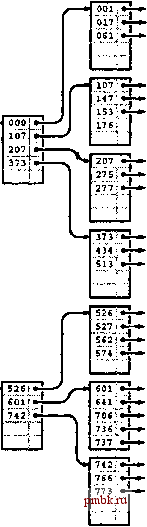

РИСУНОК 16.7 ПОСТРОЕНИЕ В-ДЕРЕВА, ЧАСТЬ 3

Продолжая приведенный пример, мы вставляем 13 ключей 574, 434, 641,207, 001,227, 061, 736,526, 562, 017, 107 и 147 в крайнее справа В-дерево из рис. 16.6. Разделение узла происходит при вставке ключей 277 (рисунок слева), 526 (рисунок в центре) и 107 (рисунок справа). Разделение узла, вызванное вставкой ключа 526, приводит также к разделению индексной страницы и к увеличению высоты дерева на единицу.

После ознакомления с этими определениями и с рассмотренными примерами деревьев, код выполнения операции search, приведенный в программе 16.2, становится вполне понятным. Для внешних узлов мы выполняем просмотр массива узлов с целью нахождения ключа, который соответствует искомому ключу, возвращая связанный с ним элемент в случае успеха и нулевой элемент в случае неудачи. Для внутренних узлов мы выполняем просмотр массива узлов для нахождения связи с уникальным поддеревом, которое могло бы содержать искомый ключ.

Программа 16.2 Поиск в В-дереве

Как обычно, эта реализация операции search для В-деревьев основывается на рекурсивной функции. Для внутренних узлов (имеющих положительную высоту) мы выполняем просмотр с целью отыскания ключа, который больше искомого, и осуществляем рекурсивный вызов поддерева, указанного предыдущей связью. Для внешних узлов (высота которых равно 0) мы ввтолняем просмотр, чтобы выяснить, содержат ли они элемент, ключ которого равен искомому.

private:

Item searchR (link h, Key v, int ht) { int j;

if (ht == 0) for (j = 0; j < h->m; j++) { if (V == h->b[j].key) return h->b[j].item; }

else

for (j = 0; j < h->m; j++)

if ((j+1 == h->m) II (V < h->b[j+l] .key) ) return searchR(h->b[j].next, v, ht-1); return nullltem;

public: Item search (Key v)

{ return searchR(head, v, HT) ; }

Программа 16.3 содержит реализацию операции insert щха В-деревьев; кроме того, в ней применяется рекурсивный подход, используемый во многих других реализациях деревьев поиска, описанных в главах 13 и 15. Эта реализация является восходящей, поскольку проверка на предмет разделения узла выполняется после рекурсивного вызова, и, следовательно, первый разделяемый узел является внешним. Разделение требует передачи новой связи вверх родительскому узлу разделяемого узла, который, в свою очередь, может нуждаться в разделении и передаче связи его родительскому узлу и т.д., возможно, вплоть до корня дерева (при разделении корня создается новый корень с двумя дочерними поддеревьями). И наоборот, в реализации 2-3-4-дерева из программы 13.6 проверка на предмет разделения выполняется перед рекурсивным вызовом, и поэтому разделение выполняется в ходе перемещения вниз по дереву. Для В-деревьев можно было бы воспользоваться также нисходящим подходом (см. упражнение 16.10). Это различие между нисходящим и восходящим подходами во многих приложениях, использующих В-деревья, несущественно, поскольку эти деревья являются очень плоскими.