О 16.4 Предположите, что затраты на зондирование составляют около а условных единиц времени, а средние затраты на поиск элемента на странице составляют около ЗМ условных единиц времени. Найдите значение М, при котором затраты на поиск в структуре индексного последовательного файла минимальны, при а/р = 10, 100 и 1000 и = 10 10 10 и 10

105 10 10

16.3 В-деревья

слов в словаре

слов в романе Моби Дик

номеров карточек социального страхования

телефонных номеров в мире

людей, когда-либо живших на Земле

10° песчинок на побережье Кони-Айленда

10 разрядов во всех

изготовленных модулях памяти

10 электронов во Вселенной

РИСУНОК 16.3 ПРИМЕРЫ РАЗМЕРОВ НАБОРОВ ДАННЫХ

Эти впечатляющие граничные значения демонстрируют, что на практике вряд ли встретится таблица символов, содержащая более 10 элементов. Даже в такой неимоверно большой базе данных элемент с заданным ключом можно было бы найти посредством менее 10 зондирований при 1 ООО-позиционном ветвлении. Даже если бы как-то удалось сохранить информацию о каждом электроне во Вселенной, 1000-позиционное ветвление позволило бы получить доступ к любому конкретному элементу через менее чем 27 зондирований.

Для построения структур поиска, которые могут быть эффективны в динамических ситуациях, мы будем строить многопозиционные деревья, но при этом откажемся от ограничения, в соответствии с которым каждый узел должен иметь в точности М записей. Вместо этого выдвинем условие, что каждый узел должен иметь максимум М записей, чтобы они помещались на странице, но при этом узлы могут иметь и меньше записей. Чтобы гарантировать, что узлы имеют достаточное количество записей для обеспечения ветвления, необходимого ради предотвращения увеличения длины путей, мы потребуем, чтобы все узлы имели, по меньшей мере (скажем) по Л 2 записей, за исключением, быть может, корня, который должен иметь не менее одной записи (двух связей). Причина этого исключения для корня станет понятна при подробном рассмотрении алгоритма. Такие деревья были названы В-деревьями благодаря Байеру (Bayer) и МакКрейту (McCreight), которые в 1970 г. первыми воспЪльзовались много путевыми сбалансированными деревьями для внешнего поиска. Термин В-дерево часто используется для описания именно той структуры данных, которая строится алгоритмом, предложенным Байером и МакКрейтом; мы же будем использовать его в качестве общего термина для обозначения семейства связанных алгоритмов.

Мы уже встречались с реализацией В-дерева: из определений 13.1 и 13.2 видно, что В-деревья четвертого порядка, в которых каждый узел имеет не более 4 и не менее 2 связей, являются ни чем иным, как сбалансированными 2-3-4-деревьями, описанными в главе 13. Действительно, лежащую в их основе абстракцию можно непосредственно обобщить и реализовать В-деревья, обобщив реализации нисходящего 2-3-4-дерева, описанные в разделе 13.4. Однако, различия между внешним и внутренним поиском, упомянутые в разделе 16.1, приводят к ряду различий в реализациях. В этом разделе мы рассмотрим реализацию, которая

обобщает 2-3-4-деревья до деревьев, имеющих от М/2 до М узлов

представляет многопутевые узлы при помощи массива элементов и связей

Глава 16, Внешний поиск

реализует индекс, а не структуру поиска, содержащую элементы

выполняет восходящее разделение

отделяет индексы от элементов

Два последних свойства в этом перечне несущественны, однако удобны во многих ситуациях и обычно встречаются в реализациях В-деревьев.

На рис. 16.4 показано абстрактное 4-5-6-7-8-дерево, являющееся обобщением 2-3-4-дерева из раздела 13.3. Обобщение очевидно: 4-узлы имеют три ключа и четыре связи, 5-узлы - четыре ключа и пять связей и т.д., при использовании одной связи для каждого возможного интервала между ключами. Поиск начинается с корня и выполняется переход от одного узла к другому с определением соответствующего интервала для искомого ключа в текущем узле. Далее осуществляется выход по соответствующей связи, чтобы добраться до следующего узла. Поиск заверщается попаданием, если искомый ключ отыскивается в любом рассмотренном узле, и промахом, если нижняя часть дерева достигается без попадания. Подобно тому как это было возможно в 2-3-4-деревьях, новый ключ можно вставить в нижнюю часть дерева после выполнения поиска, если по дороге вниз по дереву выполняется разделение полных узлов: если корень - 8-узел, он заменяется 2-узлом, связанным с двумя 4-узлами. Затем, каждый раз когда встречается А:-узел, он заменяется {к + 1)-узлом, соединенным с двумя 4-узлами. Этот подход гарантирует наличие места для вставки нового узла в случае достижения нижней части дерева.

Или же, как описывалось в разделе 13.3 применительно к 2-3-4-деревьям, разделение можно выполнять снизу вверх: вставка реализуется через поиск и помещение нового ключа в нижний узел, если только последний не является 8-узлом - в этом случае он делится на два 4-узла со вставкой среднего ключа и двух связей в его родительский узел. Восходящее разделение выполняется до тех пор, пока не встретится узел-потомок, отличный от 8-узла.

Путем замены в предьщущих двух абзацах 4 на Л 2, а 8 - на Л/, приведенные описания преобразуются в описания поиска и вставки для Л 2-...-Л/-деревьев при любом положительном целочисленном значении М, кратном 2 (см. упражнение 16.9).

( ABCD )-С FGH Г ( J К L М N оТ) ( RST ) ( V W X Y Z~) РИСУНОК 16.4 4-5-6-7-8-ДЕРЕВО

На рисунке показано обобщение 2-3-4-деревьев, построенных из узлов с от 4 до 8 связей (и от 3 до 7 связей, соответственно). Как и в случае 2-3-4-деревьев, мы поддерживаем высоту деревьев постоянной за счет разделения 8-узлов с использованием либо нисходящего, либо восходящего алгоритма. Например, для вставки в показанное дерево еще одного J следовало бы сначала разделить 8-узел на два 4-узла, а затем вставить Мв корень, преобразуя его в 6-узел. Если дело доходит до разделения корня, то не остается ничего другого, кроме как создание нового корня, который будет 2-узлом. В результате корень освобождается от ограничения, что узлы должны иметь по меньшей мере четыре связи.

Определение 16.2 В-дерево порядка М - это дерево, которое либо пусто, либо состоит из к-узлов с к-1 ключами и к связями с деревьями, представляющими каждый из к ограниченных ключами интервалов, и обладающее следующими структурными свойствами: к должно находиться в интервале между 2 и М для корня и между М/2 и М для любого другого узла; все связи с пустыми деревьями должны находиться на равном расстоянии от корня.

Алгоритмы В-деревьев строятся на основе этого базового набора абстракций. Как и в главе 13, существует значительная свобода в выборе конкретных представлений таких деревьев. Например, можно использовать расширенное RB-представление (см. упражнение 13.69). Для внешнего поиска мы используем еще более простое представление в виде упорядоченного массива, при условии, что значение М достаточно велико, чтобы Л/-узлы заполняли страницу. Коэффициент ветвления равен, по меньшей мере, М/2, поэтому, как следует из леммы 16.1, количество зондирований, необходимое для выполнения любого поиска или вставки, по сути, постоянно.

Вместо того чтобы реализовать только что описанный метод, рассмотрим вариант, обобщающий стандартный индексный указатель, рассмотренный в главе 16.1. Мы храним ключи со ссылками на элементы на внешних страницах в нижней части дерева, а копии ключей со ссылками на страницы - на внутренних страницах. Мы вставляем новые элементы в нижнюю часть, а затем используем базовую абстракцию М/2-...-М дерева. Когда страница содержит М записей, мы разделяем ее на две страницы с М/2 записями в каждой и вставляем ссылку на новую страницу в родительскую страницу. При разделении корня мы создаем новый корень с двумя дочерними узлами, тем самым увеличивая высоту дерева на I.

На рис. 16.5-16.7 показано В-древо, которое было построено в результате вставки ключей, показанных на рис. 16.1 (в приведенном порядке) в первоначально пустое дерево при Л/= 5.

176J

6oij Y-

153 и

176И

siT

706N

ООО!

ioil-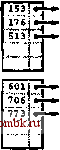

РИСУНОК 16.5 ПОСТРОЕНИЕ В-ДЕРЕВА. ЧАСТЬ 1

В этих примерах показаны шесть вставок в первоначально пустое В-дерево, построенное из страниц, которые могут содержать пять ключей и связей, при использовании ключей, являющихся 3-значными восьмеричными числами (9-разрядными двоичными числами). Ключи в страницах хранятся по порядку. Шесть вставок приводят к разделению на два внешних узла с тремя ключами в каждом и внутренний узел, служащий в качестве индекса: его первый указатель указывает на страницу, содержащую все ключи, которые больше или равны ключу ООО, но меньше ключа 601, а второй указатель - на страницу, содержащую все ключи, которые больше или равны ключу 601.