С помощью TST-деревьев легко рещается еще несколько аналогичных задач. Например, можно посетить все ключи в структуре данных, которые отличаются от ключа поиска не более чем в одной позиции цифры (см, упражнение 15,59). Операции этого типа требуют больших затрат или невозможны в случае применения других реализаций таблиц символов. Эти и многие другие задачи, когда не требуется строгое соответствие со строкой поиска, будут подробно рассматриваться в части 5,

Patricia-деревья предоставляют несколько аналогичных преимуществ; основное практическое преимущество TST-деревьев по сравнению с patricia-деревь-ями заключается в том, что они обеспечивают доступ к байтам, а не к разрядам ключей. Одна из причин, почему это различие рассматривается как преимущество, связана с тем, что предназначенные для этого машинные операции реализованы во многих компьютерах, а С++ обеспечивает непосредственный доступ к байтам символьных строк в стиле С. Другая причина состоит в том, что в некоторых приложениях работа с байтами в структуре данных естественным образом отражает байтовую ориентацию самих данных в некоторых приложениях - например, при решении задачи поиска частичного соответствия, описанной в предыдущем абзаце (хотя, как будет показано в главе 18, поиск частичного соответствия можно ускорить за счет продуманного использования доступа к разряда).

Исходя из желания избежать однопутевого ветвления в TST-деревьях, стоит заметить, что большинство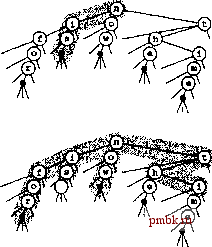

РИСУНОК 15.19 ПОИСК ЧАСТИЧНОГО СООТВЕТСТВИЯ В TST-ДЕРЕВЬЯХ

Для нахождения всех ключей в TST-дереве, которые соответствуют шаблону i* (верхний рисунок), мы выполняем поиск / в BST-дереве для первого символа. В данном примере мы находим слово is (единственное слово, соответствующее шаблону), пройдя две однопутевых ветви. Для поиска в соответствии с менее строгим шаблоном наподобие *о * (нижний рисунок) в BST-дереве первого символа мы посещаем все узлы, но в дереве второго символа только те, которые соответствуют символу о, со временем выходя на слова for и now.

однопутевых ветвлений происходит на концах ключей

и не происходит, если развить структуру до стандартной реализации многопутевого trie-дерева, в которой записи хранятся в листьях, помещенных в самом верхнем уровне trie-дерева различения ключей. Можно также поддерживать индексацию байтов, подобно тому как это делается в patricia-деревьях (см, упражнение 15,65), однако для простоты мы опускаем это изменение. Комбинация многопутевого ветвления и представления в виде TST-дерева и сама по себе достаточно эффективна во многих приложениях, но свертывание однопутевого ветвления в стиле patricia-деревьев еще больше повышается производительность в тех случаях, когда ключи, скорее всего, совпадают с длинными последовательностями (см. упражнение 15,72),

Еще одно простое усовершенствование поиска, основанного на использовании TST-деревьев, - использование большого явного многопутевого узла в корне. Для этого проще всего хранить таблицу R TST-деревьев: по одному для каждого возможного значения первой буквы в ключах. Если значение R невелико, можно использовать первые две буквы ключей (и таблицу размером /?). Чтобы этот метод был эф-

фективен, ведущие цифры ключей должны быть равномерно распределенными. Результирующий гибридный алгоритм поиска соответствует тому, как человек мог бы искать фамилии в телефонном справочнике. Вначале принимается многопутевое рещение ( Так, посмотрим, слово начинается с А ), вслед за чем, вероятно, принимается несколько двухпутевых рещений ( Оно должно располагаться перед Andrews, но после Aitken ), после чего сравнивается следующий символ ( Algonquin, ...Нет, Algoritms отсутствует, поскольку ни одно слово не начинается с Algor! ).

Программы 15.10-15.12 включают в себя основанную на применении TST-дерева реализацию операций search и insert, в которой используется /?-путевое ветвление в корне и хранение элементов в листьях (чтобы не было однопутевых ветвей, если ключи различны). Скорее всего, эти программы будут относиться к наиболее быстрым программам выполнения поиска с использованием строковых ключей. Лежащая в их основе структура TST-дерева может поддерживать также набор других операций.

Программа 15.10 Определения типов узлов в гибридном TST-дереве

Этот код определяет структуры данных, связанные с программами 15.11 и 15.12, которые предназначены для реализации таблицы символов с использованием TST-деревьев. В корневом узле используется Я-путевое ветвление: корень - это массив heads, состоящий из Я связей и индексированный по первым цифрам ключей. Каждая связь указывает на TST-дерево, построенное из всех ключей, которые начинаются с соответствующих цифр. Этот гибрид сочетает в себе преимущества trie-деревьев (быстрый поиск при помощи индексации, реализуемый в корне) и TST-деревьев (эффективное использование памяти, обусловленное существованием по одному узлу для каждого символа, не считая корня).

struct node { Item item; int d; node *1, *m, *r; node (Item x, int k)

{ item = x; d = k; 1 = 0; m = 0; r = 0; } node (node* h, int k)

{ d = k; 1 = 0; m = h; r = 0; } int internal 0

{ return d != NULLdigit; }

typedef node *link; link heads[R]; Item nullltem;

Программа 15.11 Вставка в гибридное TST-дерево для АТД таблицы символов

В этой реализации операции insert с использованием TST-деревьев элементы хранятся в листьях, что, по существу, является обобщением программы 15.3. В ней Я-путевое ветвление испо;1Ьзуется для первого символа, а отдельные TST-деревья - для всех слов, начинающихся с каждого символа. Если поиск завершается на нулевой связи, мы создаем лист для хранения элемента. Если поиск завершается в листе, мы создаем внутренние узлы, необходимые для различения найденного и искомого ключей.

private:

link split (link p, link q, int d) { int pd = digit (p->item. key 0 , d) , qd = digit(q->item.key 0, d) ; link t = new node (nullltem, qd) ;

if (pd < qd)

{ t->m - q; t->l = new node(p, pd) ; } if (pd = qd)

{ t->m = split(p, q, d+1); } if (pd > qd)

{ t->m = q; t->r = new node(p, pd) ; } return t;

link newext(Item x)

{ return new node(x, NULLdigit); } void insertR (links h. Item x, int d) { int i = digit(x.key 0 , d) ; if (h = 0)

{ h = new node (newext (x) , i) ; return; } if (!h->internal())

{ h = split (newext (x) , h, d) ; return; } if (i < h->d) insertR(h->l, x, d) ; if (i == h->d) insertR(h->m, x, d+1); if (i > h->d) insertR(h->r, x, d) ;

public; ST(int maxN)

{ for (int i = 0; i < R; i++) heads[i] =0; } void insert(Item x)

{ insertR(heads[digit(x.key0, 0)], x, 1); }

Программа 15.12 Поиск в гибридном TST-дереве для АТД таблицы символов

Эта реализация операции search для TST-деревьев (построенных с помощью программы 15.11) подобна поиску с применением многопутевого trie-дерева, но в ней используются только три, а не R связей для каждого узла (за исключением корня). Цифры ключа используются для перемещения вниз по дереву, которое завершается либо на нулевой связи (промах при поиске), либо в листе, содержащем ключ, который либо равен (попадание при поиске), либо не равен (промах при поиске) искомому.

private:

Item searchR (link h. Key v, int d) { if (h ~ 0) return nullltem; if (h->internal()) { int i = digit(v, d) , к = h->d;

if (i < k) return searchR(h->l, v, d) ; if (i == k) return searchR(h->m, v, d+1); if (i > k) return searchR(h->r, v, d) ;

if (v == h->item.key ()) return h->item; return nullltem;

public: Item search (Key v)

{ return searchR(heads[digit(v, 0)], v, 1); }

В таблице символов, которая разрастается до очень больших размеров, может потребоваться согласовать коэффициент ветвления с размером таблицы. В главе 16 будет показан систематический способ увеличения многопутевого trie-дерева, чтобы