ции search за время, которое пропорционально длине ключа, при затратах памяти, в худшем случае пропорциональных общему количеству символов в ключе. Однако общий объем используемой памяти может оказаться весьма большим, поскольку для каждого символа имеется около R связей. В конечном итоге необходимы более эффективные реализации. Как было показано для случая бинарных trie-деревьев, в качестве конкретного представления абстрактной структуры, которая хорошо определяет используемый набор ключей, имеет смысл рассматривать чистое trie-дерево. Далее можно исследовать и другие представления той же абстрактной структуры, которые, возможно, обеспечат более высокие показатели производительности.

Определение 15.3 Многопутевое trie-дерево - это многопутевое дерево, имеющее Связанные с каждым из его листьев ключи, которое рекурсивно определяется следующим образом: trie-дерево для пустого набора ключей представляет собой нулевую связь; trie-дерево для единственного ключа - лист, содержащий этот ключ; и, наконец, trie-дерево для набора ключей, количество которых значительно превышает 1 - внутренний узел со связями, ссылающимися на trie-деревья для ключей с каждым из возможных значений цифр, причем для конструирования поддеревьев ведущая цифра должна удаляться.

Предполагается, что ключи в структуре данных различны и ни один ключ не является префиксом другого. При выполнении поиска в стандартном многопутевом trie-дереве цифры ключа используются для направления поиска вниз по дереву. При этом возможны три исхода. Если достигнута нулевая связь, значит, имеет место промах при поиске; если достигнут лист, содержащий ключ поиска, имеет место попадание; если достигнут лист, содержащий другой ключ, имеет место промах при поиске. Все листья имеют R нулевых связей, следовательно, как упоминалось в разделе 15.2, узлы-листья и узлы, не являющиеся листьями, могут быть представлены различным образом. Такая реализация рассматривается в главе 16, а в этой главе предлагается другой подход к реализации. В любом случае аналитические результаты, полученные в разделе 15.3, являются достаточно общими, чтобы дать представление о характеристиках производительности стандартных многопутевых деревьев.

Лемма 15.6. Для выполнения поиска или вставки в стандартном R-арном trie-дереве в среднем требуется выполнение приблизительно logRN сравнений байтов в дереве, построенном из N случайных строк байтов. Количество связей в R-арном trie-дереве, построенном из N случайных ключей, приблизительно равно RN/\nR. Количество сравнений байтов, необходимое для выполнения поиска или сравнения, не превышает количества байтов в искомом ключе.

Эти результаты - ни что иное, как обобщение утверждений, приведенных в леммах 15.3 и 15.4. Их можно получить, подставив в доказательствах этих лемм R вместо 2. Однако, как упоминалось ранее, для выполнения точного математического анализа требуются исключительно сложные математические выкладки.

Характеристики производительности, указанные в лемме 15.6, представляют крайний случай компромисса между временем выполнения и занимаемым объемом памяти. С одной стороны, имеется большое количество неиспользуемых нулевых связей - лишь несколько узлов вблизи вершины дерева используют более одной-двух из своих связей. С другой стороны, высота дерева невелика. Предположим, например.

что используется типичное значение /?==256 и имеется jV случайных 64-разрядных ключей. В соответствии с леммой 15.6 для выполнения поиска потребуется (lgjV)/8 сравнений символов (максимум 8) и при этом будет задействовано менее A1N связей. Если объем доступной памяти не офаничен, этот метод предоставляет весьма эффективную альтернативу. Для этого примера зафаты на выполнение поиска можно было бы сократить до 4 сравнений символов, приняв /=65536, однако при этом пофебовалось бы свыше 5900 связей.

В разделе 15.5 мы вернемся к стандартным многопутевым деревьям. В остальной части этого раздела рассматривается альтернативное представление trie-деревьев, построенных программой 15.7: trie-дерево тернарного поиска (ternary search trie - TST), или просто TST-дерево, полная форма которого показана на рис. 15.16. В TST-дереве каждый узел содержит символ и три связи, соответствующие ключам, текущие цифры которых меньше, равны и больше символа узла. Подход эквивалентен реализации узлов trie-дерева в виде BST-деревьев, в который в качестве ключей используются символы, соответствующие ненулевым связям. В стандартных trie-деревьях существования из профаммы 15.7 узлы trie-дерева представляются R+\ связью, и выводы о символе, представленном каждой ненулевой связью, делаются на основании его индекса. В соответствующем TST-дереве существования все символы, соответствующие ненулевым связям, явно появляются в узлах - мы находим символы, соответствующие ключам, только при прохождении по средним связям.

Алгоритм поиска для TST-деревьев существования столь прост, что читатели вполне могли бы описать его самостоятельно. Алгоритм вставки несколько сложнее, но прямо отражает вставку в trie-деревьях существования. Для выполнения поиска первый символ в ключе сравнивается с символом в корне. Если он меньше, поиск продолжается по левой связи, если больше - по правой, а если равен, поиск выполняется вдоль средней связи и осуществляется переход к следующему символу ключа. В любом случае алгоритм применяется рекурсивно. Поиск завершается промахом, если встречается нулевая связь или конец искомого ключа встречается раньше, чем NULLdigit. Поиск завершается попаданием, если пересекается средняя связь в узле, символ которого - NULLdigit. Для вставки нового ключа выполняется поиск, а затем добавляются новые узлы для символов в заключительной части ключа, как это имело место в trie-деревьях. Подробности реализации этих алгоритмов приведены в профамме 15.8, а на рис. 15.17 показаны TST-деревья, соответствующие trie-деревьям из рис. 15.15.

Продолжая использовать соответствие между деревьями поиска и алгоритмами сортировки, мы видим, что TST-деревья соответствуют фехпутевой сортировке, точно так же как BST-деревья соответствуют быстрой сортировке, trie-деревья - бинарной быстрой сортировке, а М-путевые trie-деревья - М-путевой сортировке. Структура рекурсивных вызовов для трехпутевой сортировки, показанная на рис. 10.13, представляет собой TST-дерево для этого набора ключей. Проблема нулевых связей, характерная для trie-деревьев, похожа на проблему пустых корзин, характерную для поразрядной сортировки; фехпутевое ветвление обеспечивает эффективное решение обоих проблем.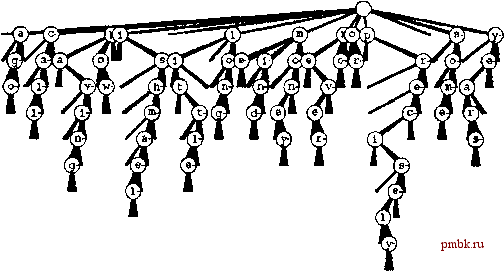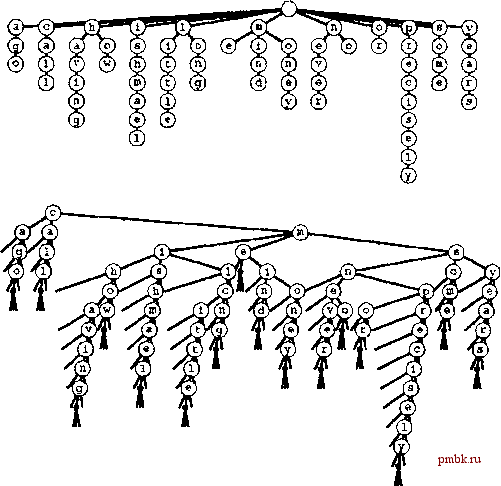

РИСУНОК 15.16 СТРУКТУРЫ TRIE-ДЕРЕВЬЕВ СУЩЕСТВОВАНИЯ

На этих рисунках показаны три различных реализации trie-дерева существования для 16 слов call те ishmael some years ago never mind how long precisely having little or no money: 26-nymeeoe trie-дерево существования (вверху); абстрактное trie-дерево с удаленными нулевыми связями (в центре); представление в виде TST-depeea (внизу). 26-путевое trie-дерево содержит слишком много связей, в то время как TST-depeeo служит эффективным представлением абстрактного trie-дерева. В двух верхних trie-деревьях предполагается, что ни один ключ не является префиксом другого. Например, добавление ключа not привело бы к потере ключа по. Для решения этой проблемы в конец каждого ключа можно добавить нулевой символ, как показано на примере TST-depeea на нижнем рисунке.