15.46 Измените программу поиска с использованием patricia-дерева (программа 15.4), чтобы в процессе перемещения вниз по дереву она сравнивала ключи с целью повышения производительности обнаружения попаданий при поиске. Экспериментально оцените эффективность произведенного изменения (см. упражнение 15.45).

15.47 Воспользуйтесь patricia-деревом для построения структуры данных, которая может поддерживать АТД таблицы существования для -разрядных целых чисел (см. упражнение 15.32).

15.48 Создайте программу, которая преобразует patricia-дерево в стандартное trie-дерево с такими же ключами, и наоборот.

15.4 Многопутевые trie-деревья и TST-деревья

Было установлено, что производительность поразрядной сортировки можно существенно увеличить, рассматривая одновременно более одного разряда. То же самое справедливо и в отношении поразрядного поиска: исследуя одновременно по г разрядов, скорость поиска можно увеличить в г раз. Однако, существует скрытая опасность, вынуждающая применять эту идею более осторожно, чем в случае поразрядной сортировки. Проблема заключается в том, что одновременное рассмотрение г разрядов соответствует использованию узлов дерева с =2 связями, а это может приводить к значительным напрасным затратам памяти для неиспользуемых связей.

В trie-деревьях (бинарных), описанных в разделе 15.2, узлы, соответствующие разрядам ключей, имеют две связи: одну для случая, когда разряд ключа равен О, и вторую для случая, когда он равен 1. Подходящим обобщением служат /?-путевые trie-деревья, когда цифрам ключа соответствуют узлы с R связями, по одной для каждого возможного значения цифры. Ключи хранятся в листьях (узлах, все связи которых являются нулевыми). Поиск в Л-путевом trie-дереве начинается с корня и с самой левой цифры ключа, а цифры ключа используются для управления перемещением вниз по дереву. Если значение цифры равно /, выполняется перемещение вниз по /-той связи (и переход на следующую цифру). В случае достижения листа, он содержит единственный ключ в trie-дереве, ведущие цифры которого соответствуют пройденному пути, поэтому для определения того, имеет ли место попадание или промах при поиске, можно сравнить этот ключ с искомым. В случае достижения нулевой связи понятно, что имеет место промах при поиске, поскольку эта связь соответствует последовательности ведущих цифр, не найденной ни в одном ключе trie-дерева. На рис. 15.14 показано 10-путевое trie-дерево, представляющее тестовый набор десятичных чисел. Как отмечалось в главе 10, встречающиеся на практике числа обычно различаются сравнительно небольшим количеством узлов trie-дерева. Эта же особенность более общих типов ключей служит основой для ряда эффективных алгоритмов поиска.

Прежде чем создавать реализацию полной таблицы символов с несколькими типами узлов, давайте начнем изучение многопутевых деревьев с задачи таблицы существования, в которой хранятся только ключи (без каких-либо записей и связанной с ними информации). Требуется разработать алгоритмы вставки ключа в структуру данных и поиска в структуре данных с целью определения, был ли вставлен заданный ключ.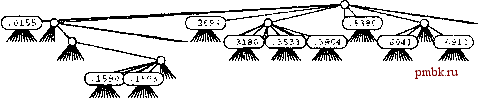

Чтобы использовать тот же интерфейс, что и для более общих реализаций таблиц символов, давайте примем соглашение, что функция поиска возвращает nullltem при промахе и фиктивный элемент, содержащий искомый ключ, при попадании. Это соглашение способствует упрощению кода и наглядному представлению структуры многопутевых trie-деревьев. В разделе 15.5 исследуются более общие реализации таблиц символов, в том числе индексация строк.

Определение 15.2 trie-дерево существования, соответствующее набору ключей, рекурсивно определяется следующим образом: trie-дерево для пустого набора ключей - нулевая связь; trie-дерево для непустого набора ключей - внутренний узел, содержащий связи, ссылающиеся на trie-дерево для каждой возможной цифры ключа, причем при построении поддеревьев ведущая цифра должна удаляться.

Для простоты в этом определении предполагается, что ни один ключ не является префиксом другого. Как правило, удовлетворение такого ограничения достигается тем, что все ключи различны и либо имеют фиксированную длину, либо содержат завершающий символ со значением NULLdigit - служебный символ, который не используется ни для каких других целей. Основное в этом определении то, что trie-деревья существования можно применять для реализации таблиц существования без сохранения внутри trie-дерева какой-либо информации. Вся информация неявно определяется внутри структуры trie-дерева. Каждый узел содержит R+\ связь (по одной для каждого возможного значения символа плюс одну связь для NULLdigit) и не содержит никакой другой информации. Для управления перемещением вниз по trie-дереву во время поиска используются цифры из ключа. Если связь с NULLdigit встречается одновременно с завершением цифр ключа, то имеет место попадание при поиске, в противном случае имеет место промах. Для вставки нового ключа поиск выполняется до тех пор, пока не встретится нулевая связь, а затем добавляются узлы для каждого из остальных символов в ключе. На рис. 15.15 показан пример 27-путевого trie-дерева; программа 15.7 содержит реализацию процедур поиска и вставки в базовом (многопутевом) trie-дереве существования.

РИСУНОК 15.14 10-ПУТЕВОЕ TRIE-ДЕРЕВО ДЛЯ ДЕСЯТИЧНЫХ ЧИСЕЛ.

На этом рисунке показано trie-дерево, которое позволяет различать набор чисел

.396465048 .353336658 .318693642 .015583409 .159369371 .691004885 .899854354 .159072306 .604144269 .269971047 .538069659

(см. рис. 12.1). Каждый узел имеет 10 связей (по одной для каждой возможной цифры). В корне связь О указывает на trie-дерево для ключей, первая цифра которых равна О (присутствует только одно такое дерево); связь 1 указывает на trie-дерево для ключей, первая цифра которых - 1 (таких деревьев два), и т.д. Ни одно из этих чисел не имеет первой цифры, равной 4, 7, 8 или 9, поэтому данные связи являются нулевыми. В дереве присутствует только по одному числу, первая цифра которого равна О, 2 ы 5, поэтому для каждой из этих цифр имеется лист, содержащий соответствующее число. Остальная часть структуры строится рекурсивно за Счет смещения на одну цифру вправо.

Программа 15.7 Поиск и ваавка в trie-дерево существования

В этой реализации операций search и insert для многопутевых trie-деревьев ключи неявно сохраняются внутри структуры trie-дерева. Каждый узел содержит R указателей на следующий, более низкий уровень trie-дерева. Когда f-той цифрой ключа будет /, перемещение выполняется вдоль /-той связи на уровне f. Функция search возвращает фиктивный элемент, содержащий переданный в аргументе ключ, если он присутствует в таблице, или nullltem в противном случав. В качестве альтернативы можно было бы изменить интерфейс, чтобы в нем использовался только тип Key, или в созданном нами классе элементов реализовать преобразование типа из Item в Key.

private: struct node

{ node **next; nodeO { next = new node* [R] ; for (int i = 0; i <

typedef node *linlc; link head;

Item searchR (link h, Key v, int d) { int i = digit(v, d) ;

if (h - 0) return nullltem; if (i == NULLdigit)

{ Item dummy(v); return dummy; } return searchR(h->next[i], v, d+1)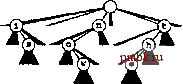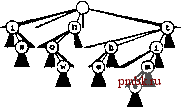

R; i++) next[i] = 0;}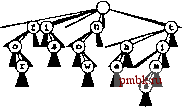

РИСУНОК 15.15 ПОИСКИ ВСТАВКА В R-ПУТЕВОМ TRIE-ДЕРЕВЕ СУЩЕСТВОВАНИЯ

26-путевое trie-дерево для слов now, is и the (рисунок вверху) имеет девять узлов: корень плюс по одному узлу для каждой буквы. На этих рисунках узлы помечены, но в структурах данных явные метки узлов не используются, поскольку метка каждого узла может быть получена, исходя из позиции его связи в массиве связей родительского узла. Для вставки ключа time в существующем узле для t

создается новая ветвь и

добавляются новые узлы для Если ключи различны и имеют фиксированную длину, ключейi,mue(рисунокв

можно обратиться к связи с конечным символом и прекра- центре); для вставки ключа щать поиск по достижении длины ключа (см. упражнение fof выполняется переход от 15.55). Мы уже встречались с примером подобного типа сорня и добавляются новые trie-дерева, когда использовали trie-деревья для описания уз - /> о и г. сортировки ключей фиксированной длины сначала по самому старшему разряду (MSD).

В определенном смысле это чисто абстрактное представление структуры trie-дерева является оптимальным, поскольку оно может поддерживать выполнение опера-

void insertR (link& h. Item x, int d) { int i = digit (X.keyO , d) ; if (h =: 0) h = new node; if (i = NULLdigit) return; insertR(h->next[i] , x, d+1);

ptiblic: ST(int naxN)

{ head =0; } Item search (Key v)

{ return searchR(head, void insert (Item x)

{ insertR(head, x, 0) ;

V, 0); }