Программа 15.4 Поиск в patricia-дереве

Рекурсивная функция searchR возвращает уникальный узел, который может содержать запись с ключом v. Она выполняет продвижение вниз по trie-дереву, используя разряды для управления поиском, но проверяет только один разряд каждого встреченного узла - указанный в поле bit. Функция прерывает поиск, встретив внешнюю связь, указывающую вверх. Функция поиска search вызывает функцию searchR, а затем проверяет ключ в этом узле для определения того, имеет ли место попадание и промах при поиске.

private:

Item searchR (link h, Key v, int d) {

if (h->bit <= d) return h->item; if (digit (V, h->bit) = 0)

return searchR(h->l, v, h->bit) ; else return searchR(h->r, v, h->bit);

public: Item search (Key v)

{ Item t = searchR(head, v, -1) ;

return (v == t.keyO) ? t : nullltem;

Ha рис. 15.10 показан поиск в patricia-дереве. В случае промаха, обусловленного тем, что поиск направляется по нулевой связи в trie-дереве, соответствующий поиск в patricia-дереве будет следовать несколько иным путем, нежели поиск в стандартном trie-дереве, поскольку при перемещении вниз по дереву разряды, соответствующие однонаправленному ветвлению, вообще не проверяются. В то время как поиск в trie-дереве завершается в листе, поиск в patricia-дереве завершается сравнением с тем же ключом, что и при поиске в trie-дереве, но без проверки разрядов, соответствующих однонаправленному ветвлению в trie-дереве.

Реализация вставки для patricia-деревьев отражает два случая, возникающих при вставке в trie-деревьях (см. рис. 15.11). Как обычно, информация о местоположении нового ключа извлекается из промаха при поиске. При использовании trie-деревьев промах может происходить либо из-за нулевой связи, либо из-за несовпадения ключа в листе. При использовании patricia-деревьев приходится выполнять дополнительные действия для определения требуемого типа вставки, поскольку во время поиска соответствующие однонаправленному ветвлению разряды были пропущены. Поиск в patricia-деревьях всегда завершается сравнением ключа, и этот ключ содержит требуемую информацию. Мы находим самый левый разряд, в котором отличаются искомый ключ и ключ, прервавший поиск, затем снова выполняем поиск в trie-дереве, сравнивая этот разряд с разрядами в узлах по пути поиска. Посещение узла, определяющего более старшую позицию разряда, чем у того, где различаются искомый и найденный ключи, свидетельствует о пропуске разряда во время поиска в particia-дереве, который должен был бы приводить к нулевой связи при аналогичном поиске, но в trie-дереве. Поэтому мы добавляем новый узел, чтобы обеспечить проверку этого разряда. Если не удается отыскать узел, определяющий более старшую позицию разряда, чем у того, где различаются искомый и найденный ключи, значит, поиск в patricia-дереве соответствует поиску в trie-дереве, который завершается в листе. В

таком случае мы добавляем новый узел, который различает искомый ключ и ключ, прервавший поиск. Мы всегда добавляем только один узел, ссылающийся на самый левый разряд, в котором ключи отличаются, в то время как при использовании стандартного trie-дерева для достижения этого разряда могло бы потребоваться добавление нескольких узлов с однонаправленными ветвями. Помимо обеспечения требуемого различения разрядов, новый узел будет использоваться также и для хранения нового элемента. Начальный этап построения примера trie-дерева показан на рис. 15.12,

Профамма 15.5 содержит реализацию алгоритма вставки в patricia-дерево. Код вытекает непосредственно из описания, приведенного в предыдущем абзаце, с учетом одного дополнительного обстоятельства, что выполняется просмоф связей с узлами, содержащими индексы разрядов, длина которых не превышает индекс текущего разряда и которые служат связями с внешними узлами. Код вставки просто проверяет это свойство связей, но не должен перемещать ключи или связи. На первый взгляд направленные вверх связи в patricia-деревьях кажутся странными, но выбор связей, которые должны использоваться при вставке каждого узла, удивительно прост. Суть же заключается в том, что использование одного типа узла вместо двух существенно упрощает код.

Профамма 15.5 Ваавка в patricia-дерево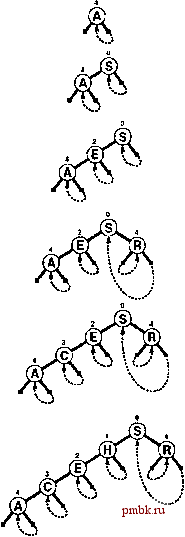

РИСУНОК 15.12 ПОСТРОЕНИЕ PATRICIA-ДЕРЕВА

Эта последовательность рисунков отражает результат вставки ключей А S Е RC Не первоначально пустое patricia-дерево. На рис. 15.11 находится результат вставки ключей I и Ne дерево, показанное на нижнем рисунке.

Процесс вставки ключа в patricia-дерево начинается с поиска. Функция searchR из программы 15,5 приводит к уникальному ключу в дереве, который должен отличаться от вставляемого. Мы определяем самый левый разряд, в котором отличаются этот и искомый ключи, а затем при помощи рекурсивной функции InsertR перемещаемся вниз по дереву и вставляем новый узел, содержащий v в этой позиции.

В функции insertR имеется два случая, которые соответствуют случаям, проиллюстрированным на рис, 15.11, Новый узел может замещать внутреннюю связь (если ключ поиска отличается от ключа, найденного в позиции разряда, который был пропущен) или внешнюю связь (если разряд, который отличает искомый ключ от найденного, не потребовался для различения найденного ключа от всех других ключей в trie-дереве).

private:

link insertR (link h, Item x, int d, link p) { Key V = X.keyO ;

if ((h->bit >= d) II (h->bit <= p->bit)) {

link t = new node(x); t->bit = d; t->l = (digit(V, t->bit) ? h : t) ; t->r = (digit(v, t->bit) ? t : h) ; return t;

if (digit (V, h->bit) = 0)

h->l = insertR (h->l, X, d, h) ; else h->r = insertR (h->r, x, d, h) ; return h;

public: void insert (Item x)

{ Key V = X. key () ; int i ;

Key w = searchR(head->l, v, -1).key(); if (v = w) return;

for (i = 0; digit(v, i) = digit(w, i) ; i++) head->l = insertR(head->1, x, i, head);

ST(int maxN)

{ head = new node (nullltem) ; head->l = head->r = head; }

В соответствии с принципом конструирования, все внешние узлы, расположенные ниже узла с индексом разряда к, начинаются с тех же самых к разрядов (в противном случае следовало бы создать узел с индексом разряда, который меньше к, чтобы два узла различались). Следовательно, patricia-дерево можно преобразовать в стандартное trie-дерево, создав соответствующие внутренние узлы между узлами, в которых разряды были пропущены, и заменив указывающие вверх связи на связи с внешними узлами (см. упражнение 15.48). Однако, лемма 15.2 выполняется для patricia-деревьев не полностью, поскольку присваивание ключей внутренним узлам зависит от порядка вставки ключей. Структура внутренних узлов зависит от порядка вставки ключей, а внешние связи и размещение значений ключей - нет.

Важное следствие того, что patricia-дерево представляет лежащую в его основе структуру стандартного trie-дерева, заключается в том, что рекурсивный поперечный обход дерева можно использовать для посещения узлов по порядку, как демонстрируется в программе 15.6. Мы посещаем только внешние узлы, которые выявляются за счет проверки на наличие не увеличивающихся индексов разрядов.

Программа 15.6 Сортировка в patricia-дереве

Эта рекурсивная процедура отображает записи в patricia-дереве в порядке следования их ключей. В программе предполагается, что элементы располагаются во внешних (виртуальных) узлах, которые могут быть выявлены при помощи проверки того, что индекс разряда в текущем узле не превышает индекс разряда его родительского узла. В остальном эта программа - суть реализация стандартного поперечного обхода.

private:

void showR(link h, ostreamfi os, int d) {

if (h->bit <= d) { h->item.show(os); return; } showR(h->l, OS, h->bit); showR(h->r, OS, h->bit);

public: void show(ostream& os)

{ showR(head->l, os, -1); }