О 15.20 Воспользуйтесь конструкцией union из С++ для реализации операций search и insert, в которых применяются trie-деревья с узлами, не являющимися листьями; которые содержат связи, но не содержат элементов; и с листьями, которые содержат элементы, но не содержат связей.

о 15.21 Воспользуйтесь парой производных классов для реализации операций search и insert, в которых используются trie-деревья с узлами, не являющимися листьями; которые содержат связи, но не содержат элементов; и с листьями, которые содержат элементы, но не содержат связей.

15.22 Измените программы 15.3 и 15.2 так, чтобы они сохраняли ключ поиска в машинном регистре и выполняли сдвиг на один разряд для обращения к следующему разряду при перемещении в trie-дереве на уровень вниз.

15.23 Измените программы 15.3 и 15.2 так, чтобы они поддерживали таблицу 2 tne-деревьев для фиксированной константы г, причем первые г разрядов ключа должны использоваться для индексирования таблицы, а к остальным разрядам ключа применяются стандартные алгоритмы доступа. Это изменение позволяет сэкономить около г шагов, если только таблица не содержит большого количества нулевых записей,

15.24 Какое значение следовало бы выбрать для г в упражнении 15,23 при наличии /V случайных ключей (которые достаточно длинны, чтобы их можно было считать различными)?

15.25 Создайте программу для вычисления количества узлов в trie-дереве, соответствующих данному набору различных ключей фиксированной длины, путем их сортировки и сравнения соседних ключей в отсортированном списке,

15.26 Методом индукции докажите, что

ЛХ(1-(1-2-)*)

- ЭТО решение рекуррентного соотношения наподобие быстрой сортировки, приведенного после леммы 15.3, для длины внешнего пути в случайном trie-дереве.

15.27 Из выражения леммы 15.4 получите выражение для среднего количества узлов в случайном trie-дереве.

15.28 Создайте профамму для вычисления среднего количества узлов в случайном trie-дереве, состоящем из узлов, и вывода значения с точностью до 10 , для N= \Q\ 10 10 и 10

15.29 Докажите, что высота trie-дерева, построенного из случайных строк разрядов, приблизительно равна 2 IgA. Совет: рассмофите задачу о дне рождения (см. лемму 14.2).

15.30 Докажите, что средние затраты на поиск в DST-дереве, посфоенном из случайных ключей, асимптотически приближаются к Ig/V (см. леммы 15.1 и 15,2),

15.31 Измените программы 15,2 и 15.3 так, чтобы они обрабатывали строки разрядов переменной длины с единственным ограничением, что в структуре данных не должны храниться записи с дублированными ключами. В частности, решите в рамках этого соглашения возвращать значение bit(v, d) для случая, когда d больше длины V.

15.32 Воспользуйтесь trie-деревом для построения структуры данных, которая может поддерживать АТД таблицы существования для w-разрядных целых чисел. Программа должна поддерживать операции construct, insert и search при условии, что insert и search принимают целочисленные аргументы, а search возвращает nuUItem.keyO в случае промаха и полученный аргумент в случае попадания при поиске.

15.3 pdtricid-деревья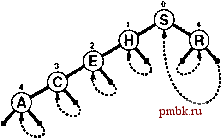

Основанный на trie-деревьях поиск, описанный в разделе 15.2, обладает двумя недостатками. Во-первых, однонаправленное ветвление приводит к созданию дополнительных узлов в trie-дереве, что кажется необязательным. Во-вторых, в trie-дереве присутствуют два различных типа узлов, что приводит к усложнениям (см. упражнения 15.20 и 15.21). В 1968 г. Моррисон (Morrison) изобрел способ ликвидации обоих проблем за счет применения метода, который назвал patricia (practical algorithm to retrieve information coded in alphanumeric - практический алгоритм получения информации, закодированной алфавитно-цифровыми символами). Моррисон разработал свой алгоритм в контексте приложений, использующих индексирование по строкам, наподобие рассмотренных в разделе 15.5, но этот алгоритм не менее эффективен и в плане реализации таблицы символов. Подобно DST-дере-вьям, patricia-деревья позволяют выполнять поиск ключей в дереве, содержащем всего vV узлов; подобно деревьям, они требуют выполнения всего лищь около IgvV сравнений разрядов и одного сравнения полного ключа для выполнения одного поиска, а также поддерживают другие операции с АТД. Более того, эти характеристики производительности не зависят от длины ключей, и структура данных подходит для ключей переменой длины.

Начиная со структуры данных стандартного trie-дерева, мы избегаем однонаправленного ветвления благодаря применению простого приема: в каждый узел помещается индекс разряда, который должен проверяться с целью выбора пути из этого узла. Таким образом, мы переходим непосредственно к разряду, в котором должно приниматься важное рещение, пропуская сравнения разрядов в узлах, в которых все ключи в поддереве имеют одинаковое значение этого разряда. Более того, внещние узлы исключаются при помощи еще одного простого приема: данные хранятся во внутрен-

РИСУНОК 15.10

ПОИСК В PATRICIA-ДЕРЕВЕ

При успешном поиске ключа R=10010 в этом pairicia-depeee выполняется перемещение вправо (поскольку нулевой разряд равен 1), затем влево (поскольку 4 разряд равен 0), что приводит к ключу R (единственному ключу в дереве, начинающемуся с последовательности 1***0). По пути вниз в дереве выполняется проверка только тех разрядов ключа, которые указаны цифрами над узлами (ключи в узлах игнорируются). При первой встрече связи, которая указывает вверх в дереве, искомый ключ сравнивается с ключом в узле, указанном идущей вверх связью, поскольку это единственный ключ в дереве, который может быть равен иско.чому ключу. При безуспешном поиске ключа 1=01001 выполняется перемещение влево от корня (поскольку нулевой бит равен 0), затем по правой (направленной вверх) связи (поскольку первый бит равен 1) и выясняется, что ключ Н (единственный ключ в дереве, начинающийся с последовательности 01) не равен I.

них узлах, а связи с внешними узлами заменяются связями, которые указывают в обратном направлении вверх на требуемый внутренний узел в trie-дереве. Эти два изменения позволяют представлять trie-деревья как бинарные деревья, состояшие из узлов с ключом и двумя связями (а также дополнительным полем под индекс); такие деревья называются patricia-деревъями. При использовании patricia-деревьев ключи хранятся в узлах, как при использовании DST-деревьев, а обход дерева выполняется в соответствии с разрядами искомого ключа, но для управления поиском нет необходимости использовать ключи в узлах при перемещении вниз по дереву. Они хранятся там просто для возможного обращения к ним впоследствии, при достижении нижней части дерева.

Как было вскользь отмечено в предыдущем абзаце, отследить работу алгоритма проще, если вначале принять во внимание, что стандартные trie-деревья и patricia-деревья можно считать различными представлениями одной и той же абстрактной структуры trie-дерева. Например, trie-деревья, показанные на рис. 15.10 и на верхней схеме рис. 15.11, иллюстрирующие поиск и вставку для patricia-деревьев, представляют ту же абстрактную структуру, что и trie-деревья на рис. 15.6. В алгоритмах поиска и вставки для patricia-деревьев используется, создается и поддерживается конкретное представление АТД trie-дерева, отличающееся от используемого в алгоритмах поиска и вставки, которые рассматривались в разделе 15.2. Тем не менее, лежащая в их основе абстракция остается той же самой.

Программа 15.4 содержит реализацию алгоритма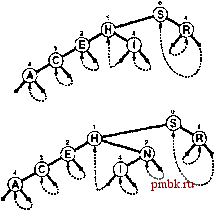

РИСУНОК 15.11 ВСТАВКА В PATRICIA-ДЕРЕВО

Чтобы вставить ключ 1в приведенный на рис. 15.10 пример patricia-дерева, мы добавляем новый узел для проверки 4 разряда, поскольку ключи Н=01000 и 1=01001 отличаются только этим разрядом (рисунок вверху). В процессе последующего поиска в trie-дереве, который достигает нового узла, необходимо проверить ключ Н (левую связь), если 4 разряд ключа поиска равен 0; если этот разряд равен 1 (правая связь), следует проверить ключ I. Для вставки ключа N=01110 (рисунок внизу) мы добавляем новый узел между ключами Н и I для проверки 2 разряда, поскольку именно этот разряд отличает Nom Ни I.

поиска в patricia-дереве. Используемый метод отличается от поиска в trie-дереве в трех отношениях: не существует никаких явных нулевых связей, в ключе проверяется не следующий разряд, а указанный, и поиск завершается сравнением ключа в точке, в которой выполняется перемещение по дереву вверх. Легко проверить, указывает ли связь вверх, поскольку индексы разрядов в узлах (по определению) увеличиваются по мере перемещения вниз по дереву. При выполнении поиска он начинается от корня и перемещение выполняется вниз по дереву с использованием индекса разряда в каждом узле для определения разряда в искомом ключе, который следует проверять - если этот разряд равен 1, перемещение выполняется вправо, а если О - влево. При перемещении вниз по дереву ключи в узлах вообще не проверяются. Со временем встречается связь, указывающая вверх: каждая направленная вверх связь указывает на уникальный ключ в дереве, содержащий разряды, которые могли бы направить поиск вдоль этой связи. Таким образом, если ключ в узле, указанный первой направленной вверх связью, равен искомому ключу, поиск является успешным; в противном случае он будет безуспешным.