Для успешного поиска ключа Н = 01000 в этом примере trie-дерева (верхние! рисунок) выполняется перемещение влево от корня (поскольку первый разряд в двоичном представлении ключа равен 0), затем вправо (поскольку второй разряд равен 1), где происходит обнаружение Н, который является единственным ключом в дереве, начинающимся с последовательности 01. Ни один ключ в trie-дереве не начинается с 101 или 11; эти последовательности разрядов ведут к нулевым связям, находящимся в узлах, которые не являются листьями.

Для вставки ключа I (нижний рисунок) потребуется добавить три узла, не являющиеся листьями: узел, соответствующий последовательности 01, с нулевой связью, соответствующей последовательности 011; узел, соответствующий 010, с нулевой связью, которая соответствует 0101; и узел, соответствующий последовательности 0100, с ключом Н = 01000 в листе слева и с ключом I = 01001 в листе справа от него.

Программа 15.3 Вставка в trie-дерево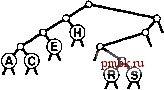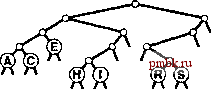

РИСУНОК 15.6 ПОИСК И ВСТАВКА В TRIE-ДЕРЕВЕ

Ключи в trie-дереве хранятся в листьях (узлах с обоими нулевыми связями); нулевые связи в узлах, которые не являются листьями, соответствуют последовательностям разрядов, не найденным ни в одном ключе trie-дерева.

Для вставки нового узла в trie-дерево вначале, как обычно, выполняется поиск. В случае промаха возможны два варианта.

Если промах имел место не в листе, нулевая связь, приведшая к выявлению промаха, как обычно, заменяется связью с новым узлом.

Если промах имел место в листе, функция split используется для создания по одному нового внутреннему узлу для каждой разрядной позиции, в которой ключ поиска и найденный ключ совпадают. Процесс завершается созданием одного внутреннего узла для самой левой разрядной позиции, в которой эти ключи различаются. Оператор switch в функции split преобразует два проверяемых разряда в число для управления четырьмя возможными случаями. Если разряды одинаковы (случай ООг = О или На = 3), разделение продолжается; если разряды различны (случай Ola = 1 или Юг = 2), разделение прекращается.

private:

link split (link p, link q, int d)

{ link t = new node (nullltem) ; t->N = 2;

Key V = p->item.key 0 ; Key w = q->item. key () ; switch (digit (v, d) *2 + digit (w, d)) { case 0: t->l = split(p, q, d+1); break; t->l = p; t->r = q; break; t->r = p; t->l = q; break; t->r = split(p, q, d+1); break;

case 1: case 2: case 3:

return t;

void insertR(link& h. Item x, int d)

{ if (h == 0) { h = new node(x); return; } if (h->l ==x 0 && h->r = 0)

{ h = split(new node(x), h, d); return; }

if (digit (X. key О , d) = 0)

insertR(h->l, X, d+1) ; else insertR(h->r, x, d+1);

piiblic: ST(int maxN)

{ head = 0; } void insert (Item item)

{ insertR(head, item, 0) ;

Мы не обращаемся к нулевым связям в листьях и не храним элементы в узлах, не являющихся листьями, поэтому можно сократить объем используемой памяти, применив union или пару производных классов для определения узлов, как принадлежащих к одному из этих двух типов (см. упражнения 15.20 и 15.21). Пока стоит пойти более простым путем, используя единственный тип узлов, который имел место в BST-деревьях, DST-деревьях и других структур бинарных деревьев, внутренние узлы которых характеризуются нулевыми ключами, а листья - нулевыми связями, памятуя, что при необходимости можно воспользоваться памятью, теряемой из-за этого упрощения. В разделе 15.3 будет рассмотрено усоверщен-ствование алгоритма, исключающее потребность в нескольких типах узлов, а в главе 16 приводится реализация, в которой применяется union.

Теперь давайте рассмотрим основные свойства trie-деревьев, вытекающие из определения и приведенных примеров.

Лемма 15.2 Структура trie-дерева не зависит от порядка вставки ключей: для каждого данного набора различных ключей существует уникальное trie-дерево.

Этот основополагающий факт, который можно доказать методом математической индукции, примененным к поддеревьям - отличительная особенность trie-деревьев: для всех остальных рассмотренных структур деревьев поиска создаваемое дерево зависит как от набора ключей, так и от порядка их вставки.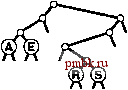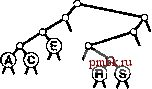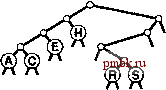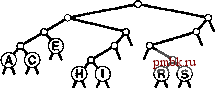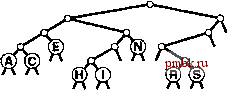

РИСУНОК 15.7 ПОСТРОЕНИЕ TRIE-ДЕРЕВА

На этой последовательности рисунков показан результат вставки ключей ASERCHINe первоначально пустое trie-дерево.

Левое поддерево trie-дерева содержит все ключи, ведущий разряд которых равен О, а правое поддерево - все ключи, ведущий разряд которых равен 1. Это свойство trie-деревьев обусловливает прямое соответствие с поразрядным поиском: при поиске с использованием бинарного trie-дерева файл делится соверщено так же, как при бинарной быстрой сортировке (см. раздел 10.2). Такое соответствие становится оче-

ВИДНЫМ при сравнении trie-дерева, показанного на рис. 15.6, со схемой разделения на рис. 10.4 (с учетом незначительного различия в ключах); это аналогично соответствию между поиском с использованием бинарного дерева и быстрой сортировкой (см. главу 12).

В частности, в отличие от DST-деревьев, trie-деревья не обладают свойством упорядоченности ключей, поэтому операции sort и select в таблице символов могут быть реализованы непосредственно (см. упражнения 15.17 и 15.18). Более того, trie-деревья столь же хорошо сбалансированы, как и DST-деревья.

Лемма 15.3. Для выполнения вставки или поиска случайного ключа в trie-дереве, построенном из N случайных (различных) строк разрядов, требуется в среднем около IgN сравнений разрядов. В худшем случае количество сравнений разрядов не превышает количество разрядов в искомом ключе.

К анализу trie-деревьев необходимо подходить очень внимательно в связи с требованием, что ключи должны быть различными, или, в более обшем случае, что ни один ключ не должен быть префиксом другого ключа. Одна из простых моделей, соответствующая этому условию, требует, чтобы ключи были случайной (бесконечной) последовательностью разрядов - из нее выбираются разряды, необходимые для построения trie-дерева.

Тогда производительность для среднего случая можно обосновать, исходя из следующих вероятностных соотношений. Вероятность того, что каждый из Л ключей в случайном trie-дереве отличается от случайного ключа поиска по меньшей мере в одном из / ведущих разрядов, равна

Вычитание этого значения из 1 дает вероятность того, что один из ключей в trie-дереве совпадает с ключом поиска во всех / ведущих разрядах. Другими словами.

ЭТО вероятность того, что для выполнения поиска требуется выполнение более / сравнений разрядов. В соответствии с элементарными соотношениями теории вероятностей для />0 сумма вероятностей того, что случайная переменная будет больше 1, совпадает со средним значением этой случайной переменной, и, следовательно, средние затраты на поиск определяются выражением

t>0

Воспользовавшись элементарной аппроксимацией (1 - \lxf~ е\ находим, что затраты на поиск должны быть приблизительно равны

t>0