встретится внешний узел. Программа 15.1 содержит реализацию операции поиска (search); реализация операции вставки (insert) аналогична. Вместо того чтобы для сравнения ключей использовать операцию <, мы исходим из предположения о наличии функции digit, обеспечивающей доступ к отдельным разрядам ключей. Этот код буквально совпадает с кодом реализации поиска в бинарном дереве (см. программу 12.8), но, как будет показано, имеет существенно иные характеристики производительности.

Программа 15.1 Бинарное DST-дерево

Чтобы разработать реализацию таблицы символов, в которой используются DST-деревья, мы изменили реализации операций search и insert в стандартном BST-дереве (см. программу 12.8), что должно быть заметно в этом примере операции search. Для принятия решения о том, следует ли выполнять перемещение влево или вправо, вместо сравнения полных ключей выполняется проверка единственного (ведущего) разряда ключа. Рекурсивные вызовы функции имеют третий аргумент, позволяющий смещать вправо позицию проверяемого разряда при перемещении вниз по дереву. Для проверки разрядов используется функция digit, как было описано в разделе 10.1. Эти же изменения применяются к реализации операции insert; в остальном используется код программы 12,8.

private: Item searchR(link

h, Key V, int d)

if (h == 0) return nullltem;

if (v == h->item.key 0 ) return h->item;

if (digit (V, d) ==0)

return searchR(h->l, v, d+1) ; else return searchR(h->r, v, d+1);

public: Item search (Key v)

{ return searchR(head, v, 0); }

В главе 10 было показано, что при использовании поразрядной сортировки особое внимание должно быть уделено совпадающим ключам; то же самое справедливо и по отношению к поразрядному поиску, В этой главе предполагается, что все значения ключей в таблице символов являются различными. Это предположение не ведет к нарушению общности, поскольку для подержания приложений, содержащих записи с дублированными ключами, можно воспользоваться одним из методов, рассмотренных в разделе 12.1. При исследовании поразрядного поиска важно сосредоточиться на различных значениях ключей, поскольку значения ключей являются важными компонентами нескольких структур данных, которые рассматриваются в дальнейшем.

На рис, 15,1 приведены двоичные представления однобуквенных ключей, используемых на остальных рисунках этой главы. На рис. 15.2 показан пример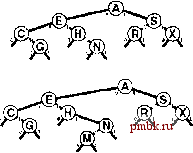

РИСУНОК 15.2 DST-ДЕРЕВО И ВСТАВКА

При выполнении безуспешного поиска ключа М=01101 в этом примере DST-depeea (вверху) мы перемещаемся влево от корня (поскольку первый разряд в двоичном представлении ключа содержит 0), а затем вправо (поскольку второй разряд содержит 1), затем вправо, влево и завершаем поиск на нулевой связи под ключом N. Для вставки ключа М(внизу) мы заменяем нулевую связь в месте завершения поиска связью с новым узлом, как это делается при вставке в BST-дерево.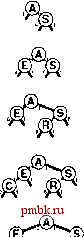

вставки в DST-дерево, а на рис. 15.3 - процесс вставки ключей в первоначально пустое дерево.

Разряды ключей управляют поиском и вставкой, но обратите внимание, что DST-деревья не обладают свойством упорядоченности, характерным для BST-деревьев. Другими словами, ключи в узлах слева от данного не обязательно меньше, а ключи в узлах справа от данного не обязательно больше ключей данного узла, как это было бы в BST-дереве с различными ключами. Ключи слева от данного узла действительно меньше ключей справа от него - если узел находится на уровне к, все они совпадают в первых к разрядах, но следующий разряд равен О для ключей слева и 1 для ключей справа - но сам ключ узла может быть наименьшим, наибольшим или любым в диапазоне всех ключей из поддерева этого узла.

DST-деревья характеризуются тем, что каждый ключ размещается где-то вдоль пути, определенного разрядами ключа (следующими слева направо). Этого свойства достаточно, чтобы реализации операций search и insert в программе 15.1 работали правильно.

Предположим, что ключи - слова фиксированной длины, каждое из которых состоит из w разрядов. Требование, чтобы ключи были различными, обусловливает, что N = 2*, и обычно предполагается, что Л значительно меньше 2 , поскольку в противном случае имело бы смысл использовать поиск с индексированием по ключу (см. раздел 12.2). Этому условию соответствует множество реальных задач. Например, использование DST-деревьев вполне подходит для таблицы символов, содержащей вплоть до 10 записей с 32-разрядными ключами (но, скорее всего, не 10 записей), или любое количество записей с 64-разрядными ключами. DST-деревья работают также и в случае ключей переменной длины; отложим подробное рассмотрение этого случая до раздела 15.2, где будет рассматриваться и ряд других альтернатив.

Производительность для худшего случая деревьев, построенных по методу поразрядного поиска, значительно выше производительности для худшего случая BST-деревьев, если количество ключей велико, а длина ключей мала по сравнению с их количеством. Вероятней всего, во многих приложениях (например, если ключи образованы случайными значениями разрядов) длина самого длинного пути в DST-дереве оказывается сравнительно небольшой. В частности, самый длинный путь ограничивается длиной самого длинного ключа; более того, если ключи имеют фиксированную длину, то время поиска ограничивается длиной. Сказанное иллюстрируется на рис. 15.4.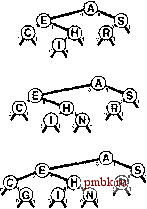

РИСУНОК 15.3 ПОСТРОЕНИЕ DST-ДЕРЕВА

На этой

последовательности рисунков показан результат вставки ключей ASERCHINGe первоначально пустое DST-дерево.

Лемма 15.1 Для выполнения поиска или вставки в DST-дереве, построенном из N случайных ключей, требуется около \$N сравнений в среднем и около 2 IgN сравнений в худшем случае. Количество сравнений никогда не превышает количество разрядов в ключе поиска.

Утверждения этой леммы для случайных ключей можно доказать при помощи рассуждений, которые аналогичны приведенным для более естественной задачи в следующем разделе, поэтому здесь мы предоставляем читателям самостоятельно вывести доказательство (см. упражнение 15.30). Доказательство основывается на интуитивном представлении о том, что невидимая часть случайного ключа с равной вероятностью должна начинаться с О или 1 разряда, поэтому половина приходится на любую сторону любого ключа. При каждом перемещении вниз по дереву мы используем разряд ключа, поэтому ни для какого поиска в DST-дере-ве не может требоваться больше сравнений, чем разрядов в ключе поиска. Для типового случая, когда имеются w-разрядные слова и количество ключей Л значительно меньше общего возможного количества ключей, равного 2 длины путей близки к IgN. Поэтому для случайных ключей количество сравнений значительно меньше количества разрядов в ключах.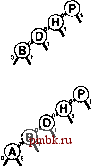

РИСУНОК 15.4 DST-ДЕРЕВО ДЛЯ ХУДШЕГО СЛУЧАЯ

В этой последовательности рисунков отображены результаты вставки ключей Р 10000, Н =01000,0 = 00100, в = 00010 uA = 00001 в первоначально пустое DST-дерево. Последовательность деревьев кажется вырожденной, но длина пути ограничивается длиной двоичного представления ключей. Ни один 5-разрядный ключ, за исключением 00000, не приводит к дальнейшему увеличению высоты дерева.

На рис. 15.5 показано большое DST-дерево, образованное случайными 7-разрядными ключами. Это дерево почти идеально сбалансировано. Использование DST-де-ревьев заманчиво во многих реальных приложениях, поскольку эти деревья обеспечивают практически оптимальную производительность даже при решении очень сложных задач, требуя лишь минимальных усилий на реализацию. Например, DST-дерево, построенное из 32-разрядных ключей (или четырех 8-разрядных символов), гарантировано требует менее 32 сравнений, а DST-дерево, построенное из 64-разрядных ключей (или восьми 8-разрядных символов), гарантировано требует менее 64 сравнений, даже при наличии миллионов ключей. Для большого значения подобные гарантии сравнимы с теми, которые обеспечивают красно-черные (RB-) деревья, но для их реализации требуются почти такие же усилия, как и для реализации стандартных BST-деревьев (которые могут гарантировать только производительность, пропорциональную Л). Это свойство делает DST-деревья привлекательной альтернативой использованию сбалансированных деревьев для практической реализации функций search и insert в таблице символов, при условии наличия эффективного доступа к разрядам ключей.