пример, а на рис. 13.26 показано конструирование списка пропусков для тех же ключей, которые показаны на рис. 13.24, но вставленных в порядке возрастания. Подобно рандомизованным BST-деревьям, стохастические свойства списков пропусков не зависят от порядка вставки ключей.

Лемма 13Л0 Для поиска и вставки в рандомизованный список пропусков с параметром t в среднем требуется около (/ log, )/2 = ( (2 Ig О) IgA сравнений.

Мы ожидаем, что список пропусков должен иметь около log,yV уровней, поскольку log,A больше наименьшего значения у, для которого t- = N. На каждом уровне мы ожидаем, что на предыдущем уровне было пропущено около t узлов, а перед переходом на следующий уровень придется пройти приблизительно половину из них. Как видно из примера на рис. 13.25, количество уровней мало, но точное аналитическое обоснование этого не столь элементарно (см. раздел ссылок).

Лемма 13 Л1 Списки пропусков имеют в среднем (t/ (t- \))N связей.

На нижнем уровне имеется N связей, N/t связей - на первом уровне, около N/связей - на втором уровне и т.д., при общем количестве связей в списке равном примерно

N{\ + \/t+ \/t+ \/t\..) = N/(\ - 1/0

Выбор подходящего значения / немедленно приводит к необходимости отыскания компромисса между временем выполнения и занимаемым объемом памяти. При / = 2 в списках пропусков требуется в среднем около IgA сравнений и 2N связей - этот уровень производительности сравним с лучшей производительностью при использовании BST-деревьев. Для больших значений / время поиска и вставки удлиняется, но дополнительный объем памяти, требуемый для связей, уменьшается. Продифференцировав выражение из леммы 13.10, мы находим, что

а в ш S

ЗШШжШШИ

3*Ё я. ЖШи I

РИСУНОК 13.24 ПОСТРОЕНИЕ СПИСКА ПРОПУСКОВ

Эта последовательность рисунков показывает результат вставки элементов с ключами А SER CHING в первоначально пустой список пропусков. Узлы содержат j связей с вероятностью 1/2-.

выбор значения / = е ми-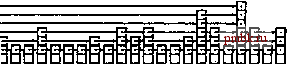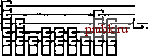

ffiffiSM

РИСУНОК 13.25 БОЛЬШОЙ СПИСОК ПРОПУСКОВ

Этот список пропусков - результат вставки в случайном порядке 50 ключей в первоначально пустой список. Доступ к каждому из ключей можно получить, следуя вдоль не более чем 7 связей.

нимизирует ожидаемое количество сравнений, требуемое для выполнения поиска в списке пропусков.

В следующей таблице приведены значения коэффициента TVlgTVB выражении, определяющем количество сравнений, необходимых для конструирования таблицы из Л элементов:

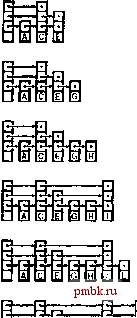Если для рекурсивного выполнения сравнений, следования связям и перемещения вниз требуются затраты, которые существенно отличаются от приведенных значений, можно выполнить более точные расчеты (см. упражнение 13.83).

Поскольку время выполнения поиска определяется логарифмической зависимостью, перерасход памяти можно уменьшить до объема, не слишком превышающего требуемый для односвязных списков (если объем памяти офани-чен), увеличив значение t. Точная оценка времени выполнения зависит от распределения относительных затрат на следование связям в списках и на переход вниз на следующий уровень. Мы вернемся к этому компромиссу между временем и объемом памяти в главе 16 при рассмотрении проблемы индексирования очень больших файлов.

Реализация других функций таблиц символов с помощью списков пропусков не представляет сложности. Например, в программе 13.10 приведена реализация функции remove, в которой применяется та же рекурсивная схема, которая использовалась для функции insert в программе 13.9. Для выполнения удаления мы разрываем связь узла со списком на каждом уровне (где он связывался для функции insert). Затем мы освобождаем узел после разрыва его связи с нижней частью списка (в отличие от его создания перед пересечением списка для вставки). Для реализации операции join списки объединяются (см. упражнение 13.78); для реализации

операции select к каждому узлу добавляется поле, содержащее количество узлов, пропущенных его связью самого высокого уровня (см. упражнение 13.77).

Программа 13.10 Удаление в списках пропусков

Для удаления узла с заданным ключом из списка пропусков мы разрываем его связь на каждом уровне, где находим связь к нему, а затем удаляем его по достижении нижнего уровня.

РИСУНОК 13.26 ПОСТРОЕНИЕ СПИСКА ПРОПУСКОВ, СОДЕРЖАЩЕГО УПОРЯДОЧЕННЫЕ КЛЮЧИ Эта последовательность рисунков показывает результат вставки элементов с ключами АСЕ GHINRSe первоначально пустой список пропусков. Стохастические свойства списка не зависят от порядка вставки ключей.

private:

void removeR (link t. Key v, int k) { link X = t->next[k];

if (! (x->item.key() < v)) {

if (v == x->item. key ())

{ t->next[k] = x->next[k]; } if (k == 0) { delete x; return; } removeR(t, v, k-1); return;

removeR(t->next[k] , v, k) ;

p\iblic: void remove (Item x)

{ removeR (head, x.keyO, 1?N) ; }

Хотя СПИСКИ пропусков легко обобщить в качестве систематического способа быстрого перемещения по связному списку, важно понимать, что лежащая в основе структура данных - всего лишь альтернативное представление сбалансированного дерева. Например, на рис. 13.27 приведено представление сбалансированного 2-3-4-дерева из рис. 13.10 в виде списка пропусков. Алгоритмы для сбалансированного 2-3-4-дерева из раздела 13.3, можно реализовать, используя абстракцию списка пропусков, а не абстракцию RB-дерева, описанную в разделе 13.4. Результирующий код несколько сложнее кода рассмотренных представлений (см. упражнение 13.80). В главе 16 мы еще вернемся к этой взаимосвязи между списками пропусков и сбалансированными деревьями.

Идеальный список пропусков, показанный на рис. 13.22 - жесткая структура, которую трудно поддерживать при вставке нового узла, как это имело место и в случае упорядоченного массива для реализации бинарного поиска, поскольку вставка сопряжена с изменением всех связей во всех узлах, следующих за вставленным. Один из способов сделать структуру более гибкой заюточается в построении списков, в которых каждая связь пропускает одну, две или три связи на расположенном ниже уровне: эта организация соответствует 2-3-4-деревьям (см. рис. 13.27). Рандомизованный алгоритм, рассмотренный в этом разделе - еще один эффективный способ уменьшения жесткости структуры; в главе 16 будут рассматриваться и другие альтернативы.

JL м1 3 f.

РИСУНОК 13.27 ПРЕДСТАВЛЕНИЕ 2-3-4-ДЕРЕВА В ВИДЕ СПИСКА ПРОПУСКОВ

Этот список пропусков - представление 2-3-4-дерева, показанного на рис. 13.10. В общем случае списки пропусков соответствуют сбалансированным многопозиционным деревьям с одной или более связью на узел (допускаются 1-узлы, не имеющие ключей и имеющие / связь). Для построения списка пропусков, соответствующего дереву, мы присваиваем каждому узлу количество связей, равное его высоте в дереве, а затем связываем узлы по горизонтали. Для построения дерева, соответствующего списку пропусков, мы группируем пропущенные узлы и рекурсивно связываем их с узлами на следующем уровне.