ный, сравнительно компактный алгоритм вставки с использованием структуры бинарного дерева, который гарантирует логарифмическую зависимость для количества шагов для всех поисков и вставок. Это одна из немногих реализаций таблиц символов, обладающих подобным свойством, и ее использование оправдано в библиотечной реализации, когда свойства обрабатываемой последовательности ключей нельзя точно охарактеризовать.

Лемма 13.8 Дпя поиска в RB-дереве с N узлами требуется менее 2 IgN + 2 сравнений.

Только для разделений, которые в 2-3-4-дереве соответствуют 3-узлу, соединенному с 4-узлом, требуется ротация в RB-дереве; таким образом эта лемма - следствие леммы 13.2. Худший случай возн1кает тогда, когда путь к точке вставки состоит из чередующихся 3-узлов и 4-узлов.

Более того, программа 13.6 устраняет небольшие накладные расходы, требуемые для балансировки, и создаваемые ею деревья почти оптимальны, поэтому она привлекательна также в качестве быстрого метода поиска общего назначения.

Лемма 13.9 Для поиска в RB-дереве с N узлами, построенном из случайных ключей, в среднем используется около 1.002 \gN сравнений.

Константа 1.002, установленная путем частичного анализа и моделирования (см. раздел ссылок), достаточно мала, чтобы можно было считать RB-деревья оптимальными для практического применения, но вопрос о том, действительно ли RB-деревья являются асимптотически оптимальными, остается открытым. Можно ли считать константу равной 1?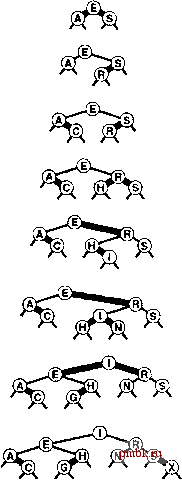

РИСУНОК 13.20 ПОСТРОЕНИЕ RB-ДЕРЕВА

Эта последовательность рисунков демонстрирует результат вставки записей с ключами AS ER CHINXe первоначально пустое RB-дерево.

Поскольку в рекурсивной реализации из программы 13.6 определенные действия выполняются перед рекурсивными вызовами, а определенные - после рекурсивных вызовов, ряд модификаций дерева выполняется при перемещении по пути поиска вниз, а ряд - на обратном пути вверх. Следовательно, в ходе одного нисходящего прохождения балансировка не выполняется. Это обстоятельство мало влияет на большинство приложений, поскольку глубина рекурсии гарантировано мала. Для некоторых приложений, связанных с несколькими независимыми процессами, обращающимися к одному и тому же дереву, может потребоваться нерекурсивная реализация, которая в каждый заданный момент времени активно оперирует только постоянным количеством узлов (см. упражнение 13.66).

Для приложения, которое хранит в дереве и другую информацию, операция ротации может оказаться дорогостоящей, возможно принуждая обновлять информацию во

РИСУНОК 13.21 БОЛЬШОЕ RB-ДЕРЕВО БИНАРНОГО ПОИСКА

Это RB-depeeo - результат вставки случайным образом упорядоченных ключей в первоначально пустое дерево. Для обнаружения всех промахов при поиске в этом дереве требуется от 6 до 12 сравнений.

всех узлах поддеревьев, затрагиваемых ротацией. Для таких приложений можно обеспечить, чтобы каждая вставка требовала не более одной ротации, используя RB-деревья для реализации восходящих 2-3-4-деревьев поиска, которые описаны в конце раздела 13.3. Вставка в эти деревья сопряжена с разделением 4-узлов вдоль пути поиска, которое требует изменений цвета, но не выполнения ротаций в RB-представ-лении, за которыми следует одна одиночная или двойная ротация (один из случаев, показанных на рис. 13.17), когда первый 2-узел или 3-узел встречается вверх вдоль пути поиска (см. упражнение 13.59).

Если в дереве необходимо поддерживать дублированные ключи, то, подобно тому как это делалось в расширенных BST-деревьях, следует разрешить элементам с ключами, равными ключу данного узла, размещаться по обе стороны от этого узла. В противном случае длинные строки дублированных ключей могут привести к серьезному дисбалансу. И снова, это наблюдение свидетельствует, что для отыскания всех элементов с данным ключом требуется специализированный код.

Как упоминалось в конце раздела 13.3, RB-представления 2-3-4-деревьев входят в число нескольких аналогичных стратегий, которые были предложены для реализации сбалансированных бинарных деревьев {см. раздел ссылок). Как было показано, балансировка деревьев достигается операциями ротации: мы рассмотрели специфическое представление деревьев, которое упрощает принятие решения о необходимости выполнения ротации. Другие представления деревьев ведут к другим алгоритмам, часть из которых мы кратко рассмотрим в данном разделе.

Старейшая и наиболее изученная структура данных для сбалансированных деревьев - сбалансированное по высоте, или AVL-, дерево, исследованное Адельсоном-Вельским (Adelson-Velskii) и Ландисом (Landis). Для этих деревьев характерно, что высоты двух поддеревьев каждого узла различаются максимум на 1. Если вставка приводит к тому, что высота одного из поддеревьев какого-либо узла увеличивается на 1, условие баланса может быть нарушено. Однако, одна одиночная или двойная ротация в любом случае вернет узел в сбалансированное состояние. Основанный на этом наблюдении алгоритм аналогичен методу восходящей балансировки 2-3-4-деревьев: для узла выполняется рекурсивный поиск, затем, после рекурсивного вызова, выполняется проверка разбалансировки и, при необходимости, одиночная или двойная ротация с целью корректирования баланса (см. упражнение 13.61). Для принятия решения о том, какие ротации нужно выполнять (если это необходимо), требуется знать, является ли высота каждого узла на 1 меньше, равна или на 1 больше высоты его родственного узла. Для прямого кодирования этой информации требуется по два

разряда на каждый узел, хотя, используя RB-абстракцию, можно обойтись и без использования дополнительного объема памяти (см. упражнения 13.62 и 13.65).

Поскольку 4-узлы не играют никакой специальной роли в алгоритме с использованием 2-3-4-деревьев, сбалансированные деревья можно строить по существу так же, используя только 2-узлы и 3-узлы. Построенные таким образом деревья называют 2-3-деревьями. Такие деревья были исследованы Хопкрофтом (Hopcroft) в 1970 г. 2-3-деревья не обладают достаточной гибкостью, чтобы можно было построить удобный алгоритм нисходящей вставки. Кроме того, RB-структура может упростить реализацию но восходящие 2-3-деревья не обеспечивают особых преимуществ по сравнению с восходящими 2-3-4-деревьями, поскольку для поддержания баланса по-прежнему требуются одиночные и двойные ротации. Восходящие 2-3-4-деревья несколько лучше сбалансированы и обладают тем преимушеством, что для каждой вставки требуется максимум одна ротация.

В главе 16 исследуется еще один важный тип сбалансированных деревьев - расширение 2-3-4-деревьев, называемое В-деревьями. В-деревья допускают существование до М ключей в одном узле для больших значений Л/и широко используются в приложениях поиска, работающих с очень большими файлами.

Мы уже определили RB-деревья их соответствием 2-3-4-деревьям. Интересно также сформулировать непосредственные структурные определения.

Определение 13.3 RB-дерево бинарного поиска - это дерево бинарного поиска, в котором каждый узел помечен как красный (R) либо черный (В), с наложением дополнительного ограничения, что никакие два красных узла не могут появляться друг за другом в любом пути от внешней связи к корню.

Определение 13.4 Сбалансированное RB-depeeo бинарного поиска - это RB-depe-во бинарного поиска, в котором все пути от внешних связей к корню содержат одинаковое количество черных узлов.

А теперь давайте рассмотрим альтернативный подход к разработке алгоритма с использованием сбалансированного дерева, заключающийся в полном игнорировании абстракции 2-3-4-дерева и формулировании алгоритма вставки, который сохраняет определяющее свойство сбалансированных RB-деревьев бинарного поиска за счет применения ротаций. Например, использование восходящего алгоритма соответствует присоединению нового узла в нижней части пути поиска с помощью R-связи, затем продвижению вверх по пути поиска с выполнением ротаций или изменений цвета, как это делалось в случаях, представленных на рис. 13.17, с целью разбиения любой встретившейся пары последовательных R-связей. Основные операции не отличаются от выполняемых в программе 13.6 и в ее восходящем аналоге, но при этом имеются незначительные различия, поскольку 3-узлы могут быть ориентированы в любом направлении, операции могут выполняться в ином порядке и различные решения в отношении различных ротаций могут приниматься с равным успехом.

Давайте подведем итоги: используя RB-деревья для реализации сбалансированных 2-3-4-деревьев, можно разработать таблицу символов, в которой операция search для ключа в файле, состоящем, скажем, из 1 миллиона элементов, может быть выполнена путем сравнения этого ключа приблизительно с 20 другими ключами. В худшем случае требуется не более 40 сравнений. Более того, с каждым сравнением связаны лишь