выполняющий прохождение вниз по дереву (аналогичный операциям вставки или поиска и вставки в стандартных BST-деревьях), с добавлением одной дополнительной проверки: если узел имеет два дочерних R-узла, он является частью 4-узла.

Столь небольшая перегрузка - основной фактор, определяющий эффективность RB-деревьев бинарного поиска.

Теперь давайте рассмотрим RB-представление двух преобразований, выполнение которых может потребоваться при встрече 4-узла. При наличии 2-узла, который соединен с 4-узлом, эту пару необходимо преобразовать в 3-узел, соединенный с двумя 2-узлами; при наличии 3-узла, соединенного с 4-узлом, пара должна быть преобразована в 4-узел, соединенный с двумя 2-узлами. Когда в нижнюю часть дерева добавляется новый узел, его можно представить в виде 4-узла, который должен быть разделен, причем его средний узел передается на один уровень вверх для вставки в нижний узел, где завершится поиск. Самой сущностью нисходящего процесса гарантируется, что этот узел должен быть либо 2-узлом, либо 3-узлом. Преобразование, требуемое при встрече 2-узла, соединенного с 4-узлом, выполняется без труда, и такое же преобразование работает применительно к 3-узлу, правильно соединенному с 4-узлом, как показано в двух первых примерах на рис. 13.17.

Остаются еще две ситуации, которые могут возникать при наличии 3-узла, соединенного с 4-узлом, как показано в последних двух примерах на рис. 13.17. (Фактически, существует четыре таких ситуации, поскольку 3-узлы другой ориентации могут также создавать зеркальные отражения представлений.) В этих случаях простое разделение 4-узла приводит к образованию двух последовательных R-связей - т.е. результирующее дерево не представляет 2-3-4-дерево в соответствии с принятыми

О

РИСУНОК 13.17 РАЗДЕЛЕНИЕ 4-УЗЛОВ В RB-ДЕРЕВЕ

В RB-depeee операция разделения 4-узла, который не является дочерним 4-узла, реализуется изменение цветов узлов дерева, образующих 4-узел с последующим возможным выполнением одной или двух ротаций. Если родительский узел является 2-узлом (верхний рисунок) или 3-узлом с подходящей ориентацией (второй сверху рисунок), ротации не потребуются. Если 4-узел располагается на центральной связи 3-узла (нижний рисунок), требуется двойная ротация; в противном случае достаточно одиночной ротации (третий сверху рисунок).

соглашениями. Эта ситуация не так уж плоха, поскольку имеется три узла, соединенные R-связями: достаточно преобразовать дерево так, чтобы R-связи указывали вниз из одного и того же узла.

К счастью, уже использованные операции ротации - это именно то, что необходимо для достижения требуемого эффекта. Давайте начнем с более простого из двух оставшихся случаев: третьего из представленных на рис. 13.17, когда 4-узел, соединенный с 3-узлом, разделяется, оставляя две идущие подряд и одинаково ориентированные R-связи. Эта ситуация не возникла бы, если бы 3-узел был ориентирован иначе. Соответственно, мы изменяем структуру дерева для изменения ориентации 3-узла и тем самым сводим этот случай ко второму, когда простого разделения 4-узла оказывается достаточно. Изменение структуры дерева для переориентации 3-узла заключается в выполнении единственной ротации с дополнительным требованием изменения цвета двух узлов.

И наконец, для обработки случая, когда 4-узел, соединенный с 3-узлом, разделяется, оставляя две идущие подряд R-связи, которые ориентированы по-разному, мы выполняем ротацию, чтобы свести этот случай к случаю с одинаково ориентированными связями, который затем обрабатывается, как было описано выше. Это преобразование сводится к выполнению тех же операций, что и при выполнении двойных ротаций влево-вправо и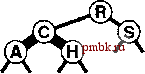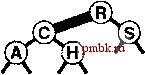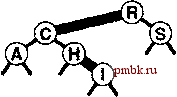

РИСУНОК 13.18 ВСТАВКА В RB-ДЕРЕВО

На этом рисунке показан результат (внизу) вставки записи с ключом I в пример RB-depeea, показанный вверху. В этом случае процесс вставки состоит из разделения 4-узла С с изменением цвета (в центре), последующим добавлением нового 2-узла в нижней части и преобразованием узла, содержащего ключ Н, в 3-узел.

вправо-влево, которые использовались для расширенных

BST-деревьев в разделе 13.2, хотя для правильной поддержки цветов потребуются незначительные дополнительные действия. Примеры операций вставки в RB-деревья приведены на рис. 13.18 и 13.19.

Программа 13.6 содержит реализацию операции insert тя RB-деревьев, выполняющую преобразования, которые обобщены на рис. 13.17. Рекурсивная реализация позволяет изменять цвета 4-узлов на пути вниз по дереву (перед рекурсивными вызовами), а затем выполнять ротации на пути вверх по дереву (после рекурсивных вызовов). Эту программу было бы трудно понять без двух уровней абстракции, разработанных для ее реализации. Несложно убедиться, что рекурсивный подход реализует ротации, изображенные на рис, 13.17; затем можно убедиться, что программа реализует высокоуровневый алгоритм в 2-3-4-деревьях - разделяет 4-узлы на пути вниз по дереву, а затем вставляет новый элемент в 2- или 3-узел в месте завершения пути поиска в нижней части дерева.

Программа 13.6 Вставка в RB-деревья бинарного поиска

Эта функция реализует вставку в 2-3-4-деревья за счет использования RB-представления. К типу node добавляется разряд цвета red (и соответствующим образом расширяется его конструктор), причем 1 означает, что узел является красным, а О - черным. На пути вниз

по дереву (перед рекурсивным вызовом) выполняется проверка на присутствие 4-узлов и их разделение с изменением разрядов цвета во всех трех узлах. По достижении нижней части дерева создается новый R-узел для вставляемого элемента и возвращается указатель на него. На пути вверх по дереву (после рекурсивного вызова) осуществляется проверка необходимости выполнения ротации. Если путь поиска содержит две R-связи с одинаковой ориентацией, выполняется единственная ротация от верхнего узла, затем разряды цвета изменяются с целью образования соответствующего 4-узла. Если путь поиска содержит две R-связи с различными ориентациями, выполняется единственная ротация от нижнего узла, в результате которой случай сводится к предыдущему.

private: int red(link x)

{ if (x == 0) return void RBinsert(links h,

0; return x->red; Item x, int sw)

if (h == 0) { if (red(h->l) { h->red = 1; if (x.keyO < {

Reinsert(h->l, if (red(h) && (red(h->l)

h = new node(x) && red(h->r)) h->l->red = 0; h->r->red h->item.key 0)

return; }

= 0; }

rotR(h); h->red = 0; h->r->red =1; }

if { }

else {

Reinsert(h->r, if (red(h) && (red(h->r)

X, 0);

red(h->l) && sw) && red(h->l->l))

rotR(h)

if {

X, 1) ;

red(h->r) && !sw) && red(h->r->r) )

rotL(h)

rotL(h) ; h->red = 0; h->l->red = 1; }

РИСУНОК 13.19 ВСТАВКА В RB-ДЕРЕВО С ИСПОЛЬЗОВАНИЕМ РОТАЦИЙ

На этом рисунке показан результат (внизу) вставки записи с ключом G в RB-depeeo, приведенное вверху. В этом случае процесс вставки состоит из разделения 4-узла с ключом I с изменением цвета (второй сверху рисунок), затем добавления нового узла в нижней части дерева (третий сверху рисунок), и, наконец, выполнения (с возвратом к каждому узлу на пути поиска - после вызовов рекурсивных

На рис. 13.20, который можно считать более подроб- ФУ<Ц*й) ротации влево в уме

. Си ротации вправо в узле R с НОИ версией рис. 13.13, показано, как программа 13.6

к к целью завершения процесса

строит RB-деревья, представляющие сбалансированные разделения 4-узла. 2-3-4-деревья при вставке тестового набора ключей. На

рис. 13.21 присутствует дерево, построенное на основе более объемного примера, чем тот, который был использован. Среднее количество узлов, посещенных во время поиска случайного ключа в этом древе, равно всего лищь 5.81. Можете сравнить это значение со значением 7.00 для дерева, построенного из этих же ключей в главе 12, и с 5.74 - наименьщим возможным для случая идеально сбалансированного дерева. Ценой всего нескольких ротаций мы получаем дерево, сбалансированное гораздо лучще любого другого, состоящего из этих же ключей. Программа 13.6 - эффектив-

public: void insert(Item { Reinsert(head,

X) X,

0); head->red =0; }