РИСУНОК 13.14 Это 2-3-4-дерево - результат 200 случайных вставок в первоначально пустое дерево. Все пути поиска в дереве содержат не более шести узлов.

ты ДЛЯ ЭТОГО были низкими, а также чтобы не приходилось идти на дополнительные затраты при каждом выполнении алгоритма. К счастью, как будет показано в разделе 13.4, существует простое представление 2-, 3- и 4-узлов, которое позволяет выполнять преобразования единообразно при небольших дополнительных затратах по сравнению со стандартным поиском в бинарном дереве.

Описанный алгоритм - всего лишь один из возможных способов поддержания баланса в 2-3-4-деревьях поиска. Разработано несколько других методов, которые позволяют достичь таких же результатов.

Например, можно выполнять балансировку снизу вверх. Вначале в дереве выполняется поиск с целью нахождения расположенного в нижней части дерева узла, к которому должен принадлежать вставляемый элемент. Если этот узел является 2-ух10м или 3-узлом, он преобразуется в 3-узел или 4-узел, как описывалось ранее. Если он - 4-узел, он делится, как и ранее (со вставкой нового элемента в один из результирующих 2-узлов в нижней части), и средний элемент вставляется в родительский узел, если тот является 2- или 3-узлом. Если родительский узел является 4-узлом, он делится на два (со вставкой среднего узла в соответствующий 2-узел), а средний элемент вставляется в его родительский узел, если тот является 2- или 3-узлом. Если узел предок также является 4-узлом, мы продолжаем такой подъем по дереву, разделяя 4-узлы до тех пор, пока на пути поиска не встретится 2-узел или 3-узел.

Такой вид восходящей балансировки можно выполнять в деревьях, которые содержат только 2- или 3-узлы (и не имеют 4-узлов). Это подход ведет к большему количеству операций разделения узлов во время выполнения алгоритма, но его проще профаммировать, поскольку приходится учитывать меньше случаев. В рамках еще одного подхода уменьшение количества операций разделения узлов достигается за счет отыскания родственных узлов, не являющихся 4-узлами, когда есть готовность приступать к разделению 4-узла.

Реализации всех этих методов требуют применения одной и той же рекурсивной схемы, как будет показано в разделе 13.14. В главе 16 рассматриваются также обобщения этих методов. Основное преимущество рассматриваемого нисходящего подхода по сравнению с другими методами заключается в том, что необходимая сбалансированность может быть достигнута в результате одного нисходящего прохода по дереву.

Упражнения

> 13.39 Нарисуйте сбалансированное 2-3-4-дерево поиска, образованное в результате вставки элементов с ключами EASYQUTIONb указанном порядке в первоначально пустое дерево с использованием метода нисходящей вставки.

[> 13.40 Нарисуйте сбалансированное 2-3-4-дерево поиска, образованное в результате вставки элементов с ключами EASYQUTIONb указанном порядке в первоначально пустое дерево с использованием метода восходящей вставки.

о 13.41 Какова минимальная и максимальная возможная высота сбалансированных 2-3-4-деревьев, содержащих узлов?

о 13.42 Какова минимальная и максимальная возможная высота сбалансированных деревьев бинарного поиска, содержащих узлов?

о 13.43 Нарисуйте все структурно различные сбалансированные 2-3-4-деревья бинарного поиска, содержащие ключей, при 2 < < 12.

13.44 Определите вероятность того, что каждое из деревьев, нарисованных в упражнении 13.43, является результатом вставки Л различных случайных элементов в первоначально пустое дерево.

13.45 Создайте таблицу, в которой будет отображаться количество деревьев из упражнения 13.43 для каждого значения Л, которые являются изоморфными в том смысле, что они могут быть преобразованы одно в другое за счет обмена поддеревьев в узлах.

[> 13.46 Опишите алгоритмы поиска и вставки в сбалансированные 2-3-4-5-6-дере-вья поиска.

[> 13.47 Нарисуйте несбалансированное 2-3-4-дерево поиска, образованное в результате вставки элементов с ключами EASYQUTIONb указанном порядке в первоначально пустое дерево с использованием следующего метода. Если поиск завершается в 2- или 3-узле, его следует преобразовать в 3- или 4-узел, как в сбалансированном алгоритме; если поиск завершается в 4-узле, соответствующую связь в этом 4-узле следует заменить новым 2-узлом.

13.4 Красно-черные деревья, или RB-деревья

Описанный в предыдущем разделе алгоритм нисходящей вставки в 2-3-4-деревья прост для понимания, но его непосредственная реализация весьма громоздка в связи со множеством различных случаев, которые могут возникать. Приходится поддерживать три различных типа узлов, сравнивать ключи поиска с каждым из ключей в узлах, копировать связи и другую информацию из узлов одного типа в узлы другого типа, создавать и удалять узлы и т.д. В этом разделе мы исследуем простое абстрактное представление 2-3-4-деревьев, которое позволяет создавать естественную реализацию алгоритмов таблиц символов с почти оптимальными гарантиями производительности для худшего случая.

Основная идея заключается в представлении 2-3-4-деревьев в виде стандартных BST-деревьев (содержащих только 2-узлы), но с добавлением к каждому узлу дополнительного информационного разряда для кодирования 3-узлов и 4-узлов. Мы будем представлять связи двумя различными типам связей: красными (red) связями (R-связями), которые объединяют воедино небольшие бинарные деревья, образующие 3-узлы и 4-узлы, и черными (black) связями (В-связями), которые объединяют воедино 2-3-4-дерево. В частности, как показано на рис. 13.15, 4-узлы представляются тремя 2-узлами, соединенными R-связями, а 3-узлы представляются двумя 2-узлами, соеди-

ненными одной R-связью. R-связь в 3-узле может быть левой или правой, следовательно, существует два способа представления каждого 3-узла.

В любом дереве каждый узел указывается одной связью, поэтому окрашивание связей эквивалентно окрашиванию узлов. Соответственно, мы используем по одному дополнительному разряду на каждый узел для хранения цвета связи, указывающей на этот узел. 2-3-4-деревья, представленные таким образом, называются красно-черными (или RB-) деревьями бинарного поиска. Ориентация каждого 3-узла определяется динамикой алгоритма, которую мы опишем. Можно было бы выдвинуть правило, что все 3-узлы наклонены одинаково, но делать это не имеет смысла. Пример RB-дерева показан на рис. 13.16. Если исключить R-связи и свернуть соединяемые ими узлы, в результате будет получено 2-3-4-дерево, показанное на рис. 13.10.

RB-деревья обладают двумя важными свойствами: (О стандартный метод search для BST-деревьев работает безо всяких изменений; ( ) существует прямое соответствие между RB-деревьями и 2-3-4-деревьями, поэтому алгоритм с использованием сбалансированного 2-3-4-дерева можно реализовать, сохранив соответствие. Таким образом, можно воспользоваться лучшим из обоих подходов: простой метод поиска, присущий стандартному BST-дереву, и простой метод вставки-балансировки, характерный для 2-3-4-дерева поиска.

Метод поиска никогда не исследует поле, представляющее цвет узла, поэтому механизм балансировки не увеличивает время, занимаемое основной процедурой поиска. Поскольку каждый ключ вставляется только один раз, но в типичном приложении его поиск может выполняться многократно, в результате общее время поиска сокращается (поскольку деревья сбалансированы) ценой сравнительно небольших дополнительных затрат (во время поисков никаких действий по балансировке не присутствует). Более того, дополнительные затраты, связанные со вставкой, невелики: действия по балансировке приходится предпринимать только при встрече 4-узлов, а в дереве количество таких узлов невелико, поскольку они всегда разделяются. Внутренним циклом процедуры вставки является код.

>

РИСУНОК 13.15 3-УЗЛЫ и 4-УЗЛЫ В RB-ДЕРЕВЬЯХ

Использование двух типов связей обеспечивает эффективный способ представления 3-узлов и 4-узлов в 2-3-4-деревьях. R-связи (жирные линии на схемах) используются для представления внутренних соединений в узлах, а В-связи (тонкие линии на схемах) - для представления связей 2-3-4-дерева. 4-узел (вверху слева) представляется сбалансированным поддеревом, состоящим из трех 2-узлов, которые соединены R-связями (вверху справа). Оба представления имеют три ключа и четыре В-связи. 3-узел (внизу слева) представляется одним 2-узлом, связанным с другим узлом (слева или справа) единственной R-связью (внизу справа). Оба представления имеют два ключа и три В-связи.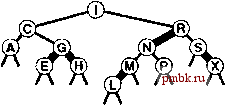

РИСУНОК 13.16 RB-ДЕРЕВО

На этом рисунке изображено RB-дерево, содержащее каючи А S R С HINGEXMPL. Ключ в таком дереве можно найти при помощи стандартного поиска в BST-деревьях. В этом дереве любой путь от корня до внешнего узла содержит три В-связи. Если свернуть узлы, соединенные R-связями, мы получим 2-3-4-дерево, показанное на рис. 13.10.