В этой главе термин 2-3-4-дерево будет применяться к сбалансированным 2-3-4-деревьям поиска (вообще говоря, в других контекстах он обозначает более общую структуру). Пример 2-3-4-дерева приведен на рис. 13.10. Алгоритм поиска ключей в таком дереве представляет собой обобщение алгоритма поиска для BST-деревьев. Чтобы выяснить, находится ли ключ в дереве, мы сравниваем его с ключами в корне: если он равен любому из них, имеет место попадание при поиске; в противном случае мы отслеживаем связь от корня к поддереву, соответствующему набору значений ключей, который должен содержать искомый ключ, и рекурсивно выполняем поиск в этом дереве. Существует ряд способов представления 2-, 3- и 4-узлов и для организации поиска соответствующей связи; отложим рассмотрение этих рещений до раздела 13.4, где приводится особенно удобная организация поиска.

Для вставки нового узла в 2-3-4-дерево можно было бы выполнить безрезультатный поиск, а затем присоединить узел, как это делалось в BST-деревьях, но при этом новое дерево оказалось бы несбалансированным. Основная особенность, делающая 2-3-4-деревья столь важными, состоит в том, что можно выполнять вставки, всегда сохраняя полную сбалансированность дерева. Например, легко видеть, что делать, если поиск прерывается на 2-узле: достаточно преобразовать его в 3-узел. Аналогично, если поиск прерывается на 3-узле, его достаточно преобразовать в 4-узел. Но что делать, если поиск прерывается на 4-узле? Рещение состоит в том, что можно освободить место для нового ключа, сохраняя сбалансированность дерева, вначале разделив 4-узел на два 2-узла, передвинув средний узел вверх к родительскому узлу данного узла. Эти три описанных случая проиллюстрированы на рис. 13.11.

А что делать, если необходимо разделить 4-узел, родительский узел которого - также 4-узел? Одним из возможных методов было разделение также и родительского узла, но узел-предок также мог бы оказаться 4-узлом и т.д. - возможно, пришлось бы разделять узлы вдоль всего дерева. Более простой подход заключается в обеспечении того, чтобы путь поиска не завершался в 4-узле за счет разделения любого 4-узла, попадающегося на пути вниз по дереву.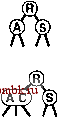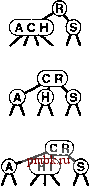

РИСУНОК 13.11 ВСТАВКА В 2-3-4-ДЕРЕВО

2-3-4-дерево, состоящее только из 2-узлов, аналогично BST-дереву (верхний рисунок). Ключ С можно вставить, преобразовав 2-узел, в котором прерывается поиск С, в 3-узел (второй сверху рисунок). Аналогично, можно вставить ключ Н, преобразовав 3-узел, в котором прерывается его поиск, в 4-узел (третий сверху рисунок). Для вставки ключа I требуется выполнение дополнительных действий, поскольку его поиск прерывается в 4-узле. Вначале мы разделяем 4-узел, передавая его средний ключ родительскому y3jiy, и преобразуем этот узел в 3-узел (четвертый сверху, выделенный рисунок). Такое преобразование создает допустимое 2-3-4-дерево, в нижней части которого появляется место для I. И, наконец, мы вставляем I в 2-узел, на котором теперь прерывается поиск, и преобразуем этот узел в 3-узел (нижний рисунок).

РИСУНОК 13.12 РАЗДЕЛЕНИЕ 4-УЗЛОВ В 2-3-4-ДЕРЕВЕ

В 2-3-4-дереве любой 4-узел, который не является дочерним узлом 4-узла, можно разделить на два 2-узла, передав его среднюю запись родительскому узлу. Присоединенный к 4-узлу 2-узел (верхний левый рисунок) становится 3-узлом, соединенным с двумя 2-узлами (вверху справа), а 3-узел, соединенный с 4-узлом (внизу слева), становится 4-узлом, соединенным с двумя 2-узлами (внизу справа).

В частности, как показано на рис. 13.12, каждый раз, когда встречается 2-узел, соединенный с 4-узлом, такая пара преобразуется в 3-узел, соединенный с двумя 2-узлами; а когда встречается 3-узел, соединенный с 4-узлом, пара преобразуется в 4-узел, соединенный с двумя 2-узлами. Разделение 4-узлов возможно потому, что можно перемещать не только ключи, но и связи. Два 2-узла имеют столько же (четыре) связей, как и 4-узел, поэтому разделение можно выполнить, не внося никаких изменений ниже (или выше) разделяемого узла. 3-узел не преобразуется в 4-узел одним лишь добавлением еще одного ключа; требуется также еще один указатель (в этом случае - дополнительная связь, созданная разделением). Очень важно, что эти преобразования являются чисто локальными: никакую часть дерева, кроме показанной на рис. 13.12, не нужно исследовать или изменять. Каждое преобразование передает один из ключей 4-узла в его родительский узел и соответствующим образом преобразует связи.

Спускаясь вниз по дереву, не нужно беспокоиться явно о родительском узле текущего 4-узла, поскольку выполняемые преобразования обеспечивают, что при прохождении каждого узла в дереве мы попадаем в узел, который не является 4-узлом. В частности, при достижении нижней части дерева мы оказываемся не в 4-узле и можем вставить новый узел, непосредственно выполнив преобразование 2-узла в 3-узел либо 3-узла в 4-узел. Вставку можно считать разделением воображаемого 4-узла в нижней части, передающим вверх новый ключ.

Одно заключительное замечание: всегда, когда корень дерева становится 4-узлом, мы просто разделяем его, преобразуя в треугольник, состоящий из трех 2-узлов, как это делалось для первого разделяемого узла в предьщущем примере. Разделение корня после вставки несколько удобнее альтернативного подхода, когда приходится ожидать, пока новая вставка выполнит разделение, поскольку не нужно заботиться о родительском узле корня. Разделение корня ( и только эта операция) приводит к увеличению высоты дерева на один уровень.

На рис. 13.13 представлено посроение 2-3-4-дерева для тестового набора ключей. В отличие от стандартных BST-деревьев, которые разрастаются вниз от вершины, эти деревья разрастаются вверх от нижней части. Поскольку 4-узлы разделяются на пути от вершины вниз, деревья называются нисходящими 2-3-4-деревьями. Этот алгоритм важен, поскольку он создает практически идеально сбалансированные деревья поиска, хотя в процессе прохождения по дереву выполняются всего лишь несколько локальных преобразований.

Лемма 13.6 При поиске в N-узловых 2-3-4-деревьях посещаются максимум IgTV + 1 узлов.

Каждый внешний узел располагается на одинаковом расстоянии от корня: выполняемые преобразования не оказывают никакого влияния на расстояние между любым узлом и корнем, за исключением случая, когда выполняется разделение корня (в этом случае расстояние между всеми узлами и корнем увеличивается на 1). Если все узлы являются 2-узлами, приведенное утверждение также справедливо, поскольку дерево подобно полному бинарному дереву; если в дереве присутствуют 3- и 4-узлы, высота может быть только меньше.

Лемма 13.7 Для вставок в N-узловых 2-3-4-деревьях в худшем случае требуется разделение менее Ig/V + 1 узлов, а в среднем, вероятно, потребуется менее одного разделения узла.

В самом худшем случае все узлы на пути к точке вставке являются 4-узлами и они все будут разделены. Но в дереве, образованном в результате случайных перестановок элементов, маловероятен не только этот худший случай, но и в среднем, вероятно, потребуется меньше операций разделения, поскольку в деревьях 4-узлы встречаются не так часто. Например, в большом дереве на рис. 13.14 все 4-узлы кроме двух расположены на нижнем уровне. До сих пор специалистам не удавалось аналитически точно проанализировать производительность 2-3-4-деревьев, но из эмпирически полученных результатов становится очевидным, что для балансировки деревьев используется очень мало разделений. Худший случай определяется только соотношением IgM и в практических ситуациях не приходится говорить даже о приближении к этому значению.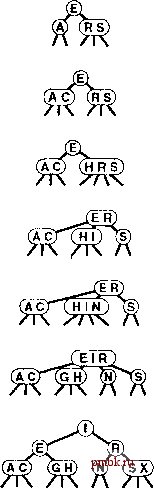

Приведенное описание достаточно для определения алгоритма поиска с использованием 2-3-4-деревьев, который гарантирует достаточно высокую производительность для худшего случая. Однако, мы находимся лишь на половине пути к реализации. Хотя можно было бы создать шпоритмы, действительно выполняющие преобразования с различными типами данных, представляющими 2-, 3- и 4-узлы, для большинства встречающихся задач это непосредственное представление не очень удобно в плане реализации. Как и в случае расширенных BST-деревьев, накладные расходы, связанные с манипулированием более сложными структурами узлов, могли бы сделать алгоритмы более медленными, чем стандартный поиск с использованием BST-деревьев. Главное назначение балансировки - обеспечение средства против наихздшего случая, но мы предпочли бы, чтобы затра-

РИСУНОК 13.13 ПОСТРОЕНИЕ 2-3-4-ДЕРЕВА

На этой последовательности рисунков показан результат вставки элементов с ключами А SERCHINGXe первоначально пустое 2-3-4-дерево. Ка.ждый встречающийся по пути поиска 4-узел разделяется, обеспечивая тем самым свободное место для нового элемента в нижней части дерева.