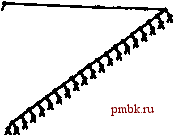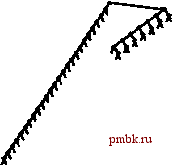РИСУНОК 13.9 БАЛАНСИРОВКА ХУДШЕГО СЛУЧАЯ РАСШИРЕННОГО ДЕРЕВА С ПОМОЩЬЮ ПОИСКА

Вставка ключей по порядку в первоначально пустое дерево с использованием вставки с расширением требует только постоянного количества шагов для выполнения одной вставки, но создает несбалансированное дерево, показанное на верхних рисунках. Последовательность рисунков слева отображает результат поиска (с расширением) наименьшего, второго, третьего и четвертого наименьших ключей в дереве. Каждый поиск уменьшает длину пути к искомому ключу (и к большинству других ключей в дереве) в два раза. Последовательность рисунков справа показана балансировка этого же худшего случая дерева с использованием последовательности случайных попаданий при поиске. Каждый поиск уменьшает вдвое количество узлов в своем пути, уменьшая длину путей поиска и множества других узлов в дереве.

!> 13.26 Сколько связей дерева должно быть изменено Ш1Я выполнения двойной ротации? Сколько связей действительно изменяется при BbinojmeHHH каждой из двойных ротаций в программе 13.5?

13.27 Добавьте в программу 13.5 реализацию операции search с расширением.

о 13.28 Реализуйте нерекурсивную версию функции вставки с расширением в программе 13.5.

13.29 Используйте программу-драйвер, созданную в упражнении 12.30, для определения эффективности расширенных BST-деревьев в качестве самоорганизующихся структур, сравнив их со стандартными BST-деревьями для распределений запросов на поиск, определенных в упражнениях 12.31 и 12.32.

о 13.30 Нарисуйте все структурно различные BST-деревья, которые могут быть образованы в результате вставки ключей в первоначально пустое дерево с использованием вставки с расширением, при 2 < N < 7.

13.31 Определите вероятность того, что каждое из деревьев в упражнении 13.30 образовано в результате вставки N случайных раз.П1чных элементов в первоначально пустое BST-дерево.

о 13.32 Определите эмпирически среднее значение и стандартное отклонение количества сравнений, используемых для обнаружения попаданий и промахов при поиске в BST-дереве, построенного в результате вставки N случайных ключей в первоначально пустое дерево с использованием вставки с расширением, при N = 10 , 10 *, 10 и 10 Не следует выполнять какие-либо поиски: просто постройте деревья и вычислите длину их путей. Являются ли расширенные BST-деревья сбалансированными в большей степени, чем произвольные BST-деревья, в меньшей степени или так же?

13.33 Усовершенствуйте программу, созданную для упражнения 13.32, чтобы она выполняла случайных поисков (скорее всего, они будут неудачными), выполняя расширение в каждом из созданных деревьев. Как расширение влияет на среднее количество сравнений, необходимых для выявления промаха при поиске?

13.34 Измените программы, созданные для упражнений 13.32 и 13.33, чтобы они измеряли время выполнения, а не просто подсчитывали количество сравнений. Проведите аналогичные эксперименты. Поясните любые изменения в выводах, получаемых из экспериментальных результатов.

13.35 Сравните расширенные BST-деревья со стандартными BST-деревьями применительно к задаче построения индекса из фрагмента реального текста, содержащего по меньшей мере 1 миллион символов. Измерьте время, требуемое для построения индекса и средние длины путей в BST-деревьях.

13.36 Определите экспериментально среднее количество сравнений для обнаружения попаданий при поиске в расширенном BST-дереве, построенном в результате вставки произвольных ключей, при Л = 10, 10*, 10 и 10.

13.37 Прибегните к экспериментальному исследованию с целью проверки идеи использования вставки с расширением вместо стандартной вставки в корень для рандомизованных BST-деревьев.

о 13.38 Нарисуйте расширенное BST-дерево, образованное в результате вставки элементов с ключами 000000000000 1 в указанном порядке в первоначально пустое дерево.

13.3 Нисходящие 2-3-4-деревья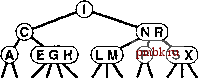

Несмотря на гарантию производительности, которую можно обеспечить при использовании рандомизованных и расширенных BST-деревьев, в обоих случаях не исключается вероятность того, что время выполнения отдельной операции поиска может определяться линейной зависимостью. Следовательно, эти методы не помогают ответить на основной вопрос в отношении сбалансированных деревьев: существует ли тип BST-дерева, для которого можно гарантировать логарифмическую зависимость времени выполнения каждой операции insert и search от размеров дерева? В этом и следующем разделах мы рассмотрим абстрактное обобщение BST-деревьев и абстрактное представление этих деревьев в виде типа BST-дерева, которые позволяют утвердительно ответить на этот вопрос.

Для гарантии того, что создаваемые BST-деревья будут сбалансированными, используемые структуры деревьев должны обладать определенной гибкостью. Для получения подобной гибкости давайте предположим, что узлы в наших деревьях могут содержать более одного ключа. В частности, мы допускаем существование 3-уз-лов и 4-узлов, которые могут содержать, соответственно, два и три ключа. 3-узел имеет три исходящие из него связи: одну ко всем элементам, ключи которых меньше обоих его ключей, одну ко всем элементам, ключи которых располагаются между двумя его ключами, и одну ко всем элементам, ключи которых больше обоих его ключей. Аналогично, 4-узел имеет 4 исходящих связи: по одной для каждого из интервалов, определенных его тремя ключами. Таким образом, узлы в стандартном BST-дереве можно было бы называть 2-узлами: они содержат один ключ и две связи. Позже мы рассмотрим эффективные способы определения и реализации базовых операций с этими расширенными узлами; а пока давайте примем, что ими можно манипулировать обычным образом, и посмотрим, как их можно собрать воедино для образования деревьев.

Определение 13.1 2-3-4-дерево поиска - это либо пустое дерево, либо дерево, содержащее три типа узлов: 2-узлы с одним ключом, левой связью к дереву с меньшими ключами и правой связью к дереву с большими ключами; 3-узлы с двумя ключами, с левой связью к дереву с меньшими ключами, средней связью к дереву, значения ключей которых лежат между значениями ключей данного узла, и правой связью к дереву с большими ключами; и 4-узлы с тремя ключами и четырьмя связями к деревьям, значения ключей которых определены диапазонами, образобанными ключами узла.

Определение 13.2 Сбалансированное 23-4дерево поиска - это 2-3-4-дерево поиска, все пустые деревья которого расположены на одинаковом расстоянии от корня.

РИСУНОК 13.10 2-3-4-ДЕРЕВО

На этом рисунке изображено 2-3-4-дерево, содержаш,ее ключи ASRC HI NGEXM PL. В таком дереве ключ можно отыскать, используя ключи в узле, расположенном в корне, для нахождения связи к поддереву, а затем продолжить рекурсивное выполнение поиска. Например, для выполнения поиска ключа Р в этом дереве потребовалось бы проследить правую связь от корня, поскольку Р больше I, затем - среднюю связь от правого дочернего дерева корня, поскольку значение Р располагается между N и R, и, наконец, завершить успешный поиск во втором узле, содержащем ключ Р.