if (h = 0)

{ h = new node(x, 0, 0, 1); return; } if (x.lceyO < h->itein.key())

{ link* hi = h->l; int N = h->N; if (hi = 0)

{ h = new node(x, 0, h, N+1); return; } if (X.keyO < hl->itejn.key())

{ splay(hl->l, X); rotR(h); } else { splay(hl->r, x); rotL(hi); } rotR(h);

>

else

{ link 4hr = h->r; int N = h->N; if (hr == 0)

{ h = new node(x, h, 0, N+1); return; } if {hr->item.key() < x.keyO)

{ splay(hr->r, x); rotL(h); } else { splay(hr->l, x); rotR(hr) ; } rotL(h);

public: void insert (Item item) { splay(head, item); )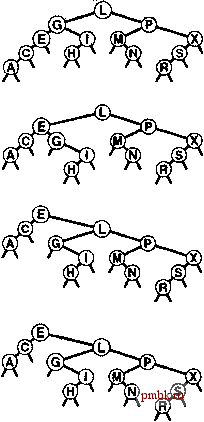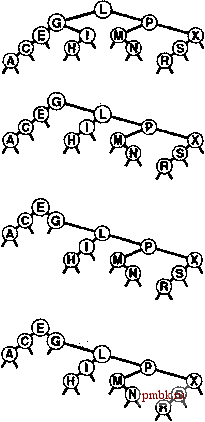

РИСУНОК 13.6 ДВОЙНАЯ РОТАЦИЯ В BST-ДЕРЕВЕ (ОРИЕНТАЦИИ ОДИНАКОВЫ)

Когда обе связи в двойной ротации ориентированы в одном направлении, существуют две возможности. При использовании стандартного метода вставки в корень вначале выполняется ротация в узле, расположенном ниже (слева); при использовании вставки со скосом вначале выполняется вставка в узле, расположенном выше (справа).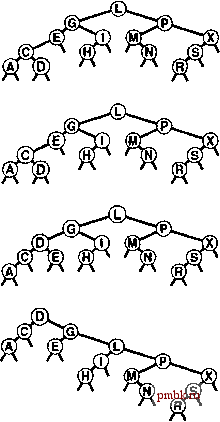

Лемма 13.4 Количество сравнений, используемых при построении расширенного дерева путем N вставок в первоначально пустое дерево, равно О (NlgN).

Это утверждение - следствие более жесткой леммы 13.5, которая будет вскоре рассмотрена.

Подразумевается, что константа в 0-нотации имеет значение 3. Например, ддя построения BST-дерева, состоящего из 100000 узлов, с использованием вставки с расширением всегда требуется менее 5 миллионов сравнений. Это не гарантирует, что результирующее дерево поиска будет хорошо сбалансировано и что каждая операция будет эффективной, но тем не менее обеспечивает весьма значительную гарантию в отношении общего времени выполнения; на практике фактическое время выполнения, скорее всего, откажется еще меньшей.

При вставке узла в BST-дерево с использованием вставки с расширением мы не только перемещаем этот узел в корень, но и перемещаем все встретившиеся узлы (в пути поиска) ближе к корню. Точнее говоря, выполняемые ротации уменьшают в два раза расстояние от корня до любого встретившегося узла. Это свойство сохраняется также при реализации операции search таким образом, чтобы во время поиска она выполняла трансформации с расширением. Некоторые пути в деревьях удлиняются: если обращение к узлам в этих путях не выполняется, указанный эффект не имеет значения. Если же мы обращаемся к узлам в длинном пути, после обращения он укорачивается в два раза; таким образом, ни один путь не может порождать больших затрат.

Лемма 13.5 Количество сравнений, требуемых для любой последовательности М операций вставки или поиска в N-узловом расширенном BST-дереве, равно

О ({N + М) \g(N + М)).

Доказательство этого утверждения, приведенное Слеатором (Sleator) и Тарьяном (Tarjan) в 1985 г. - классический пример амортизационного анализа, ал горитмов {см. раздел ссылок). Подробно он исследуется в части 8.

Лемма 13.5 представляет гарантию амортизационного алгоритма: мы гарантируем не эффективность каждой операции, но эффективность усредненных затрат всех выполненных операций. Это усредненное значение не является вероятностным; скорее можно утверждать, что общие затраты гарантированно будут низкими. Для многих приложений такого рода гарантии достаточно, но для других приложений этого может оказаться мало. Например, нельзя гарантировать время ответа для каждой

РИСУНОК 13.7 ВСТАВКА С РАСШИРЕНИЕМ

На этом рисунке изображен результат (внизу) вставки записи с ключом D в пример дерева, приведенный на верхнем рисунке, с использованием вставки в корень с расширением. В этом случае процесс вставки состоит из двойной ротации влево-вправо, за которой следует двойная ротация вправо-вправо (от вершины).

операции при использовании расширенных BST-деревьев, поскольку время выполнения некоторых операций может определяться линейной зависимостью. Если какая-либо операция занимает время, которое определяется линейной зависимостью, существует гарантия, что другие операции будут выполняться гораздо быстрее, но это - слабое утешение для клиента, который вынужден ожидать.

Предельное значение, приведенное в лемме 13.5 - предельное значение общих затрат на все операции для худшего случая: как это типично для предельных значений худших случаев, эти затраты могут быть гораздо выше фактических. Операции с расширением перемещают недавно посещенные элементы ближе к вершине дерева; поэтому этот метод привлекателен для приложений поиска, имеющих неоднородные шаблоны обращения - особенно для приложений со сравнительно небольшим, пусть даже и медленно изменяющимся, рабочим набором элементов, к которым выполняется обращение.

На рис. 13.9 приведены два примера, демонстрирующие эффективность операций расширения-ротации при балансировке дерева. На этих рисунках вырожденное дерево (построенное за счет вставки элементов в порядке их ключей) приводится в сравнительно хорошо сбалансированное состояние в результате небольшого числа операций search.

Обобщая, можно сказать, что небольшое количество выполненных поисков существенно улучшает сбалансированность дерева.

Если в дереве поддерживаются дублированные ключи, то операция с расширением может привести к тому, что элементы с ключами, равными ключу в данном узле, попадут по обе стороны от этого узла (см. упражнение 13.38). Из этого следует, что нельзя найти все элементы с данным ключом столь же легко, как это имело место в стандартных BST-деревьях. Необходимо проверить наличие дубликатов в обоих поддеревьях или воссПользоваться каким-либо альтернативным методом для работы с дублированными ключами, как было описано в главе 12.

Упражнения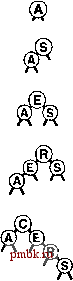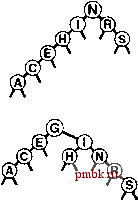

РИСУНОК 13.8 ПОСТРОЕНИЕ РАСШИРЕННОГО ДЕРЕВА

Эта последовательность рисунков демонстрирует вставку записей с ключами ASERCHINGe первоначально пустое дерево с использованием вставки с расширением.

\> 13.25 Нарисуйте расширенное BST-дерево, образованное в результате вставки элементов с ключами EASYQUTIONb указанном порядке в первоначально пустое дерево с использованием вставки с расширением.