Как и в случае с леммой 13.1, для доказательства этого утверждения требуется тщательный вероятностный анализ (см. раздел ссылок).

Доказатедьства свойств вероятностных алгоритмов требуют хорошего понимания теории вероятностей, тем не менее, понимание этих доказательств отнюдь не обязательно для программистов, использующих алгоритмы. Осмотрительный программист в любом случае проверит утверждения, подобные лемме 13.2, не зависимо от того, как они обоснованы (например, убеждаясь в качестве генератора случайных чисел или иных особенностей реализации), и, следовательно, сможет использовать эти методы со знанием дела. Рандомизованные BST-деревья - вероятно, простейщий способ поддержки АТД заполненной таблицы символов при гарантировании почти оптимальной производительности. Именно поэтому они находят применение во многих практических приложениях.

Упражнения

> 13.8 Нарисуйте рандомизованное BST-дерево, образующееся в результате вставки элементов с ключами EASYQUTIONb указанном порядке в первоначально пустое дерево при условии, что плохо выполняющая рандомизацию функция, приводящая к вставке в корень, применяется во всех случаях, когда размер дерева является нечетным.

13.9 Создайте программу-драйвер, которая 1000 раз выполняет следующий эксперимент для 7V = 10 и 100: используя профамму 13.2, вставляет ключи от О до Л- 1 (в указанном порядке) в первоначально пустое рандомизованное BST-дерево, а затем выводит статистическую функцию Х, исходя из предположения, что вероятность попадания каждого ключа в корень равна \/N (см. упражнение 14.5).

о 13.10 Укажите вероятность попадания ключа F в каждую из позиций, показанных на рис. 13.2.

13.11 Создайте программу вычисления вероятности того, что рандомизованная вставка завершается в одном из внутренних узлов данного дерева для каждого из узлов в пути поиска.

13.12 Создайте программу вычисления вероятности того, что рандомизованная вставка завершается в одном из внешних узлов данного дерева.

о 13.13 Реализуйте нерекурсивную версию функции рандомизоваиной вставки, приведенной в программе 13.2.

13.14 Нарисуйте рандомизованное BST-дерево, образующееся в результате вставки элементов с ключами EASYQUTIONb указанном порядке в первоначально пустое дерево при использовании версии программы 13.2, в которой выражение, содержащее функцию rand(), заменяется проверкой (111 % h->N) == 3 для принятия решения о применении вставки в корень.

13.15 Выполните упражнение 13.9 для версии программы 13.2, в которой выражение, содержащее функцию rand(), заменяется проверкой (111 % h->N) == 3 для принятия решения о применении вставки в корень.

13.16 Приведите последовательность рандомизованных решений, которая привела бы к построению вырожденного дерева (в котором все ключи упорядочены, а левые связи являются нулевыми) из ключей EASYQUTION. Какова вероятность возникновения этого события?

13.17 Может ли любое BST-дерево, содержащее ключи EASYQUTIO N, быть построено посредством какой-либо последовательности принятия рандомизованных рещений, если эти ключи вставляются в указанном порядке в первоначально пустое дерево? Обоснуйте свой ответ.

13.18 Определите эмпирическим путем среднее значение и стандартное отклонение количества сравнений, используемых для обнаружения попаданий и промахов при поиске в рандомизованном BST-дереве, построенном в результате вставки Л случайных ключей в первоначально пустое дерево, при Л= 10 10 *, 10 и 10.

[> 13.19 Нарисуйте BST-дерево, образующееся в результате использования программы 13.4 для удаления ключа Q из дерева, построенного в упражнении 13.4, при использовании проверки (111 % (a->N + b->N)) < a->N для принятия решения об объединении с помещением а в корень.

13.20 Нарисуйте BST-дерево, образующееся в результате вставки элементов с ключами Е А S Y в первоначально пустое дерево, вставки элементов с ключами Q U Е S Т I О N в другое первоначально пустое дерево и последующего объединения результата за счет использования программы 13.3 с выполнением проверки, описанной в упражнении 13.19.

13.21 Нарисуйте BST-дерево, образующееся в результате вставки элементов с ключами EASYQUTIONb указанном порядке в первоначально пустое дерево и последующего применения программы 13.4 для удаления ключа Q, при использовании плохо выполняющей рандомизацию функции, которая всегда возвра1#га-ет 0.

13.22 Экспериментально определите увеличение высоты BST-дерева при выполнении длинной последовательности чередующихся вставок и удалений с помощью программ 13.2 и 13.3 в дереве, состоящем из узлов, при = 10, 100 и 1000 и при выполнении Л пар вставок-удалений для каждого N.

о 13.23 Сравните результаты, полученные в результате выполнения упражнения 13.22, с результатом удаления и повторной вставки наибольшего ключа в рандомизованном дереве, состоящем из узлов, при использовании программ 13.2 и 13.3 для = 10, 100 и 1000 и при выполнении Л пар вставок-удалений для каждого N.

13.24 Модифицируйте программу из упражнения 13.22 для определения усредненного количества вызовов функции rand(), выполняемого ею для удаления одного элемента.

13.2 Расширенные деревья бинарного поиска

в методе вставки в корень, описанном в разделе 12.8, основная цель достигалась путем перемещения вновь вставленного узла в корень дерева с помощью ротации влево и вправо. В этом разделе исследуются способы модификации метода вставки в корень, чтобы ротации также в определенном смысле балансировали дерево.

Вместо того чтобы рассматривать (рекурсивно) единственную ротацию, которая перемещает недавно вставленный узел к вершине дерева, рассмотрим две ротации, которые перемещают узел из позиции в одном из дочерних узлов корня к вершине дерева. Вначале выполняется одна ротация, которая сделает узел дочерним узлом корня. Затем при помощи еще одной ротации он перемещается в корень. Существует

два принципиально различных случая, в зависимости от того, одинаково ли ориентированы две связи от корня к вставляемому узлу. На рис. 13.5 показан случай, когда ориентации различны; в правой части рис. 13.6 изображен случай, когда ориентации одинаковы. В основе обработки расширенных BST-деревьев лежит наблюдение о существовании альтернативного способа выполнения действий, когда связи от корня к вставляемому узлу ориентированы одинаково: достаточно выполнить две ротации в корне, как показано в правой части рис. 13.6.

Вставка со скосом (splay insertion) перемещает вновь вставленные узлы в корень за счет применения трансформаций, показанных на рис. 13.5 (стандартной вставки в корень, когда связи от корня к дочернему узлу в пути поиска имеют различную ориентацию) и в правой части рис. 13.6 (двух ротаций в корне, когда связи от корня к дочернему узлу в пути поиска имеют одинаковую ориентацию). Построенные таким образом BST-деревья являются расширенными BST-деревъями. Программа 13.5 содержит рекурсивную реализацию вставки с расширением; пример одиночной вставки приведен на рис. 13.7, а процесс построения примера дерева показан на рис. 13.8. Различие между вставкой с расширением и стандартной вставкой в корень может показаться несущественным, но оно достаточно важно: расширение исключает худший случай квадратичной зависимости времени выполнения, являющийся главным недостатком стандартных BST-деревьев.

Программа 13.5 Вставка с расширением в BST-деревья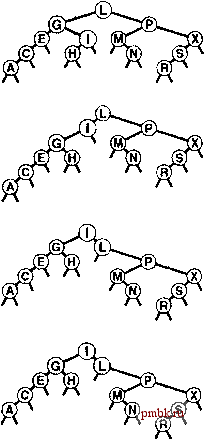

РИСУНОК 13.5 ДВОЙНАЯ РОТАЦИЯ В BST-ДЕРЕВЕ (ОРИЕНТАЦИИ РАЗЛИЧНЫ)

В этом простом дереве (вверху) в резулыпате ротации влево в угпе G, за которой следует ротация вправо в узле L, узел I помещается в корень (внизу). Эти ротации могут завершать процесс вставки в стандартном или скошенном BST-дереве.

Эта функция отличается от алгоритма вставки в корень программы 12.13 лишь одной существенной особенностью: если путь поиска проходит влево-влево или вправо-вправо, узел перемещается в корень путем двойной ротации от вершины, а не от нижней части (см. рис. 13.6).

Программа проверяет четыре варианта для двух шагов пути поиска от корня и выполняет соответствующие ротации:

влево-влево: дважды выполняет ротацию влево в корне;

влево-вправо: выполняет ротацию влево в левом дочернем узле, а затем вправо в корне;

вправо-вправо: дважды выполняет ротацию вправо в корне;

вправо-влево: выполняет ротацию вправо в правом дочернем узле, а затем ротацию влево в корне.

private: void splay (links h, Item x)