Этот результат совпадает с результатами, полученными из общего рещения вероятностных соотношений, которые были разработаны Карпом (Кагр) в 1995 г. (oif. раздел ссылок).

Например, для построения рандомизованного BST-дерева, состоящего из 100000 узлов, требуется около 2.3 миллиона сравнений, но вероятность того, что количество сравнений превысит 23 миллиона, значительно меньше 0.01 процента. Подобная гарантия производительности более чем удовлетворяет практические требования, предъявляемые к обработке реальных наборов данных такого размера. Упомянутую гарантию нельзя обеспечить при использовании стандартного BST-дерева для выполнения такой задачи: например, придется столкнуться с проблемами снижения производительности, если данные в значительной степени упорядочены, что маловероятно для случайных данных, но по множеству причин достаточно часто имеет место при работе с реальными данными.

По тем же соображениям, утверждение, аналогичное лемме 13.2, справедливо и по отношению к времени выполнения быстрой сортировки. Но в данном случае это еще более важно, поскольку отсюда следует, что затраты на поиск в дереве близки к усредненным. Независимо от дополнительных затрат на построение деревьев, стандартную реализацию BST-дерева можно использовать для выполнения операций search при затратах, которые зависят только от формы деревьев, при отсутствии вообще каких-либо дополнительных затрат на балансировку. Это свойство важно в типовых приложениях, в которых операции search гораздо более многочисленны, нежели любые другие. Например, описанное в предыдущем абзаце BST-дерево, состоящее из 100000 узлов, могло бы содержать телефонный справочник и использоваться для выполнения миллионов поисков. Можно быть почти уверенным, что каждый поиск потребует затрат, которые отличаются от усредненных затрат, равных приблизительно 23 сравнениям, лишь небольшим постоянным коэффициентом. Поэтому на практике можно не беспокоиться, что для большого количества поисков потребуется количество сравнений, приближающееся к 100000, в то время как при использовании стандартных BST-деревьев это было бы весьма актуально.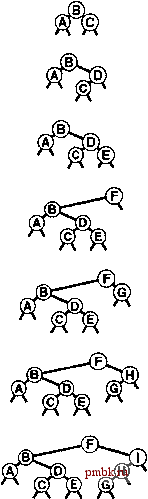

®

РИСУНОК 13.3 ПОСТРОЕНИЕ РАНДОМИЗОВАННОГО BST-ДЕРЕВА

На этих рисунках показана вставка ключей А В С D Е F G НI в первоначально пустое BST-дерево методом рандомизованных вставок. Дерево на нижнем рисунке выглядит так же. как если бы оно было построено с применением стандартного алгоритма BST-дерева при вставке этих же ключей в случайном порядке.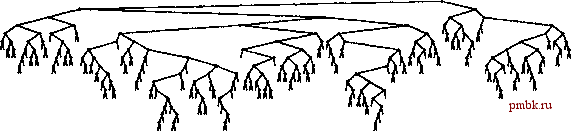

РИСУНОК 13.4 БОЛЬШОЕ РАНДОМИЗОВАННОЕ BST-ДЕРЕВО

Это BST-дерево является результатом рандомизоваиной вставки 200 элементов в порядке возрастания их ключей в первоначально пустое дерево. Дерево выглядит так, как если бы оно было построено из ключей, расположенных в случайном порядке (см. рис. 12.8).

Один ИЗ главных недостатков рандомизоваиной вставки - затраты на генерацию случайных чисел в каждом из узлов во время каждой вставки. Высокопроизводительный системный генератор случайных чисел может работать с большой нагрузкой для генерации псевдослучайных чисел с большей степенью случайности, чем требуется для BST-деревьев. Поэтому в определенных реальных ситуациях (например, если допу-шение о случайном порядке следования элементов справедливо) конструирование рандомизованного BST-дерева может оказаться более медленным процессом, чем построение стандартного BST-дерева. Подобно тому как это делалось в случае быстрой сортировки, эти затраты можно снизить, используя числа, которые не являются совершенно случайными, но не требуют больших затрат при генерации и достаточно подобны случайным числам. Тем самым минимизируется возникновение худших случаев BST-деревьев при последовательностях вставок ключей, которые вполне могут встретиться на практике (см. упражнение 13.14).

Еше один потенциальный недостаток рандомизованных BST-деревьев - необходимость наличия в каждом узле поля количества узлов поддерева данного узла. Дополнительный объем памяти, требуемый для поддержки этого поля, может оказаться чрезмерной платой для больших деревьев. С другой стороны, как было показано в разделе 12.9, это поле может требоваться по ряду других причин ~ например, для поддержки операции select или для обеспечения проверки целостности структуры данных. В подобных случаях рандомизованные BST-деревья не требуют никаких дополнительных затрат памяти и их использование представляется весьма привлекательным.

Основной принцип сохранения случайной структуры деревьев ведет также к эффективным реализациям операций remove, join и других операций для АТД таблицы символов, обеспечивая при этом создание рандомизованных деревьев.

Для объединения дерева, состояшего из N узлов, с деревом, состоящим из Л/узлов, используется базовый метод, описанный в главе 12, за исключением принятия рандомизованного решения о выборе корня исходя из того, что корень объединенного дерева должен выбираться из УУ-узлового дерева с вероятностью УУ / (Л/ + Л), а из Л/-узлового дерева - с вероятностью М / (М + N). Программа 13.3 содержит решш-зацию этой операции.

Программа 13.3 Комбинация рандомизованных BST-деревьев

В этой функции используется тот же метод, что и в программе 12.17, за исключением того, что в ней принимается рандомизованное, а не произвольное решение о том, какой узел использовать в качестве корня объединенного дерева, исходя из равной вероятности размещения корня в любом узле. Приватная функция-член fixN обновляет b->N значением, которое на 1 больше суммы соответствующих полей в поддеревьях (О для нулевых деревьев).

private: link joinR(link а, link b) {

if (a == 0) return b; if (b = 0) return a; insertR(b, a->item); b->l = joinR(a->l, b->l); b->r = joinR(a->r, b->r); delete a; fixN(b); return b;

public:

void join(ST<Itern, Key>& b) { int N = head->N;

if (rand()/(RAND MAX/(N+b.head->N)+l) < N)

head = joinR(head, b.head); else head = joinR(b.head, head) ; }

Аналогично, произвольное решение заменяется рандомизованным в алгоритме remove, как показано в программе 13.4. Этот метод соответствует нерассмотренному варианту реализации удаления узлов в стандартных BST-деревьях, поскольку он приводил бы (при отсутствии рандомизации) к несбалансированным деревьям (см. упражнение 13.21).

Программа 13.4 Удаление в раидомизоваииом BST-дереве.

Мы используем ту же функцию remove, которая применялась для стандартных BST-деревьев (см. программу 12.6), но при этом функция joinLR заменяется функцией, приведенной здесь, которая принимает рандомизованное, а не произвольное решение о замещении удаленного узла предком или потомком, исходя из того, что каждый узел в результирующем дереве с равной вероятностью может быть корнем. Чтобы правильно поддерживать счетчики узлов, в качестве последнего оператора в функции removeR необходимо также включить вызов функции fixN (см. программу 13.3) для h.

link joinLR (link a, link b) {

if (a = 0) return b; if (b == 0) return a;

if (randO/(RAND MAX/(a->N+b->N)+l) < a->N)

{ a->r = joinLR(a->r, b) ; return a; } else { b->l = joinLR (a, b->l) ; return b; }

Лемма 13.3 Создание дерева через произвольную последовательность рандомизованных операций вставки, удаления и объединения эквивалентно построению стандартного BST-дерева за счет случайной перестановки ключей в дереве.