характеристик производительности. Помимо различий, обусловленных различной природой гарантий производительности, обеспечиваемых тем или иным ш]горитмом, каждый из методов характеризуется затратами (сравнительно небольшими) времени или памяти, сопряженными с упомянутыми гарантиями; разработка АТД действительно оптимально сбалансированного дерева все еше остается предметом будуших исследований. Тем не менее, все рассматриваемые в этой главе алгоритмы весьма важны и способны обеспечить быстро выполняюшиеся реализации операций search и insert (и ряда других операций для АТД таблицы символов) в динамических таблицах символов, предназначенных для разнообразных приложений.

Упражнения

о 13.1 Реализуйте эффективную функцию, выполняюшую повторную балансировку BST-деревьев, которые не содержат поле счетчика в своих узлах.

13.2 Модифицируйте стандартную функцию вставки в BST-дерево, представленную в программе 12.8, чтобы ее можно было использовать в программе 13.1 для выполнения повторной балансировки дерева каждый раз, когда количество элементов в таблице символов достигает числа, равного степени 2. Сравните время выполнения этой программы с временем выполнения программы 12.8 при выполнении задач (/) построения дерева из N случайных ключей и (/7) поиска N случайных ключей в результирующем дереве, для УУ = 10 10*, 10 и 10.

13.3 Оцените количество сравнений, используемых программой из упражнения 13.2 при вставке возрастающей последовательности TV ключей в таблицу символов.

13.4 Покажите, что для выроженного дерева время выполнения программы 13.1 пропорционально MgN. Затем приведите максимально неоптимальный вариант дерева, при котором время выполнения программы определяется линейной функцией.

13.5 Модифицируйте стандартную функцию вставки в BST-дерево, приведенную в программе 12.8, чтобы она делила примерно пополам любой встреченный узел, который в одном из своих поддеревьев содержит менее одной четверти всех узлов. Сравните время выполнения этой программы с временем выполнения программы 12.8 при выполнении задач (/) построения дерева из N случайных ключей и ( ) поиска tV случайных ключей в результирующем дереве, для N = 10, 10*, 10 и 10.

13.6 Оцените количество сравнений, используемых программой из упражнения 13.5 при вставке возрастающей последовательности TV ключей в таблицу символов.

13.7 Расширьте реализацию, созданную в упражнении 13.5, чтобы она так же выполняла повторную балансировку при выполнении функции remove. Экспериментально определите, возрастает ли высота дерева при выполнении длиной последовательности чередующихся случайных вставок и удалений в случайном дереве, состоящем из УУ узлов при N = 10, 100 и 1000 и при выполнении пар вставок-удалений для каждого N.

13.1 Рандомизованные BST-деревья

Чтобы проанализировать затраты для случая усредненной производительности при работе с BST-де-ревьями, было сделано допущение, что элементы вставляются в случайном порядке (см. раздел 12.6). Применительно к алгоритму с использованием BST-дерева главное следствие этого допущения заключается в том, что каждый узел дерева с равной вероятностью может оказаться корневым, причем это же справедливо и по отнощению к поддеревьям. Как это ни удивительно, случайность можно включить в алгоритм, чтобы это свойство сохранялось без каких-либо допущений относительно порядка вставки элементов. Идея весьма проста: при вставке нового узла в дерево, состоящее из N узлов, вероятность появления нового узла в корне должна быть равна 1/{N + 1), поэтому мы просто принимаем рандомизованное рещение использовать вставку в корень с этой вероятностью. В противном случае мы рекурсивно используем метод для вставки новой записи в левое поддерево, если ключ записи меньще ключа в корне, и в правое поддерево - если он больше. Программа 13.2 содержит реализацию этого метода.

Если использовать нерекурсивный подход, выполнение рандомизованной вставки эквивалентно выполнению стандартного поиска ключа с принятием на каждом шаге рандомизованного решения о том, продолжить ли поиск или прервать его и выполнить вставку в корень. Таким образом, как показано на рис. 13.2, новый узел может быть вставлен в любое место на пути поиска. Это простое вероятностное объединение стандартного алгоритма BST-дерева с методом вставки в корень обеспечивает гарантированную в смысле вероятности производительность.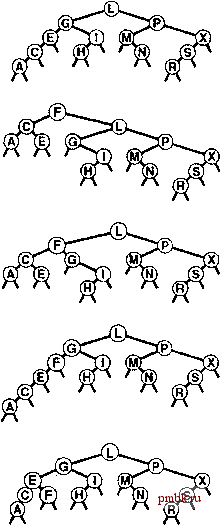

РИСУНОК 13.2 ВСТАВКА В РАНДОМИЗОВАННОЕ BST-ДЕРЕВО

Новая запись в рандомизованном BST-дереве может располагаться в любом месте пути поиска записи, в зависимости от результата рандомизованных решений, принятых во время поиска. На этом рисунке показаны возможные местоположения записи, содержащей ключ Г, при ее вставке в пример дерева (верхний

рисунок).

Лемма 13.1 Построение рандомизованного BST-дерева эквивалентно построению стандартного BST-дерева из случайно переставленных в исходном состоянии ключей. Для конструирования рандомизованного BST-дерева из N элементов используется около INXnN сравнений (независимо от порядка вставки элементов), а для выполнения поиска в таком дереве требуется приблизительно 2 1пЛ сравнений.

Каждый элемент с равной вероятностью может быть корнем дерева, и это свойство сохраняется и для обоих поддеревьев. Первая часть этого утверждения подтверждается самим методом конструирования, но для подтверждения того, что

метод вставки в корень сохраняет случайность поддеревьев, требуется тщательное вероятностное обоснование {см. раздел ссылок).

Различие между производительностью в усредненном случае для рандомизованных и стандартных BST-деревьев очень невелико, но имеет большое значение. Усредненные затраты в обоих случаях одинаковы (хотя для рандомизованных деревьев коэффициент пропорциональности несколько выше), однако для случая стандартных деревьев результат зависит от допущения о представлении элементов к вставке в случайном порядке их ключей (их вставка в любом порядке равновероятна). Это допущение не справедливо во многих практических приложениях, и, следовательно, рандомизованный алгоритм примечателен тем, что позволяет избавиться от такого допущения и вместо этого исходить из законов распределения вероятностей в генераторе случайных чисел. При вставке элементов в порядке следования их ключей, в обратном порядке или любом другом порядке, BST-дерево все равно будет рандомизо-ванным.

Программа 13.2 Вставка в рандомизованное BST-дерево

Эта функция принимает рандомизованное решение о том, использовать ли метод вставки в корень программы 12.13 или стандартный метод вставки программы 12.8. В рандомизованном BST-дереве каждый из узлов с равной вероятностью является корнем; поэтому, помещая новый узел в корень дерева размера N с вероятностью 1/(Л/ + 1), мы получаем рандомизованное дерево.

private: void insertR(links h. Item x)

{if (h == 0) { h = new node(x); return; } if (randO < RAND MAX/(h->N+l))

{ insertT(h, x); return; } if (x.keyO < h->item.key 0)

insertR(h->l, x); else insertR(h->r, x); h->N++;

public: void insert(Item x) { insertR(head, x); )

Ha рис. 13.3 показано создание рандомизованного дерева для примера набора ключей. Поскольку принимаемые алгоритмом решения являются рандомизованны-ми, вероятно, последовательность деревьев при каждом выполнении алгоритма будет иной. На рис. 13.4 отражается тот факт, что рандомизованное дерево, сконструированное из набора элементов, ключи которых упорядочены по возрастанию, выглядит так же, как стандартное BST-дерево, построенное из элементов, следующих в случайном порядке (сравните с рис. 12.8).

Существует вероятность, что при первой же возможности генератор случайных чисел может привести к неверному решению, обусловливая тем самым создание плохо сбалансированных деревьев, однако эту вероятность можно оценить математически и доказать, что она очень мала.

Лемма 13.2 Вероятность того, что затраты на создание рандо.м и зова иного BST-дерева превышают усредненные затраты в а раз, меньше е~.