Сбалансированные деревья

Описанные в предыдущей главе алгоритмы, использующие деревья бинарного поиска (BST-деревья) ус-пещно работают для щирокого множества приложений, однако их производительность существенно снижается в худщих случаях. Более того, как это ни прискорбно, на практике именно худщий случай стандартного алгоритма с использованием BST-дерева наподобие быстрой сортировки встречается чаще всего, причем когда пользователь не ожидает этого. Уже упорядоченные файлы, файлы с большим количеством дублированных ключей, упорядоченные в обратном порядке файлы или файлы с любым большим сегментом, имеющим простую структуру, могут приводить к тому, что время построения BST-дерева определяется квадратичной, а время поиска - линейной зависимостью.

В идеальном случае можно было бы сохранять деревья полностью сбалансированными, подобно дереву, показанному на рис. 13.1. Эта структура соответствует бинарному поиску и, следовательно, все поиски могут быть выполнены с использованием менее N+ 1 сравнений, но при этом поддержка динамических вставок и уттений сопряжена с большими затратами. Высокая производительность поиска гарантируется для любого BST-лерева, в котором все внешние узлы расположены в одном, в крайнем случае в двух, нижних уровнях. Существует большое множество таких BST-деревьев, поэтому в плане поддержки сбалансированности дерева имеется некоторая свобода. Если нас устраивают деревья, близкие к оптимальным, возможности еще больше расширяются. Например, существует очень много BST-деревьев, высота которых не превышает 2 IgTV. Если допустимо смягчить стандарт, но при этом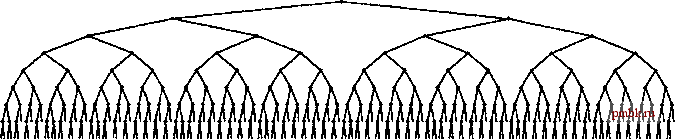

РИСУНОК 13.1 БОЛЬШОЕ ПОЛНОСТЬЮ СБАЛАНСИРОВАННОЕ BST-ДЕРЕВО

Все внешние узлы этого BST-дерева располагаются в одном из двух уровней, и для выполнения любого поиска требуется столько же сравнений, сколько использовалось бы при поиске этого же ключа методом бинарного поиска (если бы элементы хранились в упорядоченном массиве). Цель применения алгоритма с использованием сбалансированного дерева - сохранение BST-дерева максимально сбалансированным при сохранении эффективности вставки, удаления и других операций с АТД словаря.

гарантировать, что алгоритмы будут строить только такие BST-деревья, можно избежать снижения производительности для худшего случая, что было бы желательно в реальных приложениях, работающих с динамическими структурами данных. При этом производительность для среднего случая также увеличивается.

Один из подходов к повышению степени сбалансированности в BST-деревьях связан с периодическим явным выполнением их повторной балансировки. Действительно, используя рекурсивный метод, продемонстрированный в программе 13.1, большинство BST-деревьев можно полностью сбалансировать, затратив на это время, которое определяется линейной зависимостью (см. упражнение 13.4). Скорее всего, такая повторная балансировка повысит производительность для случайных ключей, но не обеспечит гарантию против квадратичной зависимости производительности выполнения операций в динамической таблице символов для худшего случая. С одной стороны, между операциями повторной балансировки время вставки для данной последовательности ключей может возрастать в квадратичной зависимости от длины последовательности; с другой стороны, повторную балансировку крупных деревьев нежелательно выполнять слишком часто, поскольку для выполнения каждой операции балансировки требуется время, которое, по меньшей мере, линейно зависит от размера дерева. Необходимость отыскания компромисса в данной ситуации затрудняет использование глобальной повторной балансировки для гарантирования высокой производительности в динамических BST-деревьях. Во всех рассматриваемых в дальнейшем алгоритмах во время обхода дерева выполняются последовательно нарастающие локальные операции, которые совместно увеличивают сбалансированность всего дерева, хотя при этом никогда не приходится выполнять обход всех узлов подобно тому, как это имеет место в программе 13.1.

Программа 13.1 Балансировка BST-дерева

Используя функцию разделения на части partR из программы 12.15, эта рекурсивная функция приводит BST-дерево в полностью сбалансированное состояние при затратах времени, которые определяются линейной зависимостью. Разделение на части выполняется с целью помещения среднего узла в корень, а затем это же выполняется для поддеревьев.

void balanceR(links h) {

if ((h == 0) II (h->N = 1)) return; partR(h, h->N/2); balanceR(h->l) ; balanceR(h->r);

Задача обеспечения гарантированной производительности для реализаций таблиц символов, основанных на использовании BST-деревьев, - превосходный повод для исследования того, что именно подразумевается под гарантированной производительностью. Будут показаны решения этой задачи, являющиеся типичными примерами трех базовых подходов к обеспечению гарантированной производительности при разработке алгоритмов: рандомизации, амортизации и оптимизации. А теперь давайте по очереди кратко рассмотрим каждый из этих подходов.

При использовании рандомизованного алгоритма принятие случайного решения встроено в сам алгоритм, что радикально уменьшает вероятность возникновения худшего случая сценария (независимо от входного массива данных). Мы уже видели типичный пример такого подхода, когда случайный элемент использовался в качестве разделяющего в алгоритме быстрой сортировки. В разделах 13.1 и 13.5 исследуются рандомизованные BST-деревья и списки пропусков - два простых c/ioco6a использования рандомизации в реализациях таблиц символов для увеличения эффективности всех операций с АТД таблицы символов. Эти алгоритмы просты и широко используются, однако они оставались неисследованными в течение нескольких десятилетий {см. раздел ссылок). Аналитическое доказательство эффективности этих алгоритмов не является элементарным, но сами алгоритмы просты для понимания, как и их реализация и практическое применение.

Амортизационный подход заключается в однократном выполнении дополнительных действий во избежание выполнения большего объема работы впоследствии, чтобы можно было обеспечить гарантированный верхний предел усредненной стоимости одной операции (обшей стоимости всех операций, разделенной на количество операций). В разделе 13.2 рассматривается расширенное дерево - вариант BST-дерева, которое можно использовать для обеспечения таких гарантий при реализации таблиц символов. Разработка этого метода послужила одним из стимулов разработки концепции амортизации {см. раздел ссылок). Этот алгоритм - вполне очевидное расширение метода вставок в корень, рассмотренного в главе 12, но аналитическое обоснование предельных значений производительности является достаточно сложным.

Отимизационный подход заключается в обеспечении гарантированной производительности каждой операции. Были разработаны различные методы, использующие этот подход, часть из которых восходит к 60-м годам. Эти методы требуют хранения в деревьях некоторой структурной информации, и, как правило, их реализация связана с определенной сложностью. В этой главе рассматриваются две простые абстракции, которые не только делают реализацию понятной, но и обеспечивают почти оптимальные верхние пределы затрат. В заключение, после исследования реализаций АТД таблиц символов с использованием каждого из этих трех подходов, обеспечивающих гарантированную высокую производительность, в главе приводится сравнение