дереву. В-третьих, можно воспользоваться ссылкой или указателем на указатель узла в качестве дескриптора. Этот метод подходит в языках С++ и С, но не во множестве других языков. В-четвертых, можно прибегнуть к ленивому подходу, помечая удаленные узлы и периодически перестраивая структуру данных, как описывалось несколько ранее.

Последняя операция с АТД таблиц символов, которую мы рассмотрим - операция join. В реализации с использованием BST-дерева это сводится к объединению двух деревьев. Как объединить два дерева бинарного поиска в одно? Существуют различные алгоритмы для выполнения этой задачи, но каждому из них присущи определенные недостатки. Например, можно было бы обойти первое BST-дерево, вставляя каждый из его узлов во второе BST-дерево (этот алгоритм является однонаправленным: функция insert во втором BST-дереве используется как параметр функции обхода первого BST-дерева), Время выполнения подобного решения не линейно, поскольку для каждой вставки может требоваться линейное время. Другой подход связан с обходом обоих BST-деревьев с целью помещения элементов в массив, объединения их и затем построения нового BST-дерева. Время выполнения этой операции может быть линейным, но это также связано с потенциально большим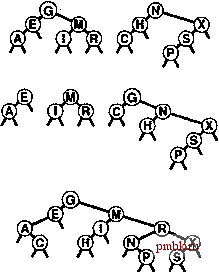

РИСУНОК 12.20 ОБЪЕДИНЕНИЕ ДВУХ BST-ДЕРЕВЬЕВ

На этой схеме показан результат (внизу) объединения двух примеров BST-деревьев (вверху). Вначале мы вставляем корень G первого дерева во второе дерево, используя вставку в корень (второй сверху рисунок). У нас остаются два поддерева, ключи которых меньше G, и два поддерева, ключи которых больше G. Объединение обоих пар (рекурсивно) обеспечивает конечный результат (рисунок внизу).

массивом.

Программа 12.17 - компактная, линейная по затратам времени рекурсивная реализация операции join. Вначале мы вставляем корень первого BST-дерева во второе BST-дерево, используя метод вставки в корень. Эта операция дает два поддерева, ключи которых заведомо меньше этого корня, и два поддерева, ключи которых заведомо больше этого корня, поэтому требуемый результат получается путем объединения (рекурсивного) первой пары в левое поддерево корня, а второй пары - в правое поддерево корня (!). Каждый узел может быть корневым максимум при одном рекурсивном вызове, поэтому общее время определяется линейной зависимостью.

Программа 12.17 Объединение двух BST-деревьев

Если одно из BST-деревьев пустое, второе будет представлять результат. В противном случае два BST-дерева объединяются путем выбора (произвольного) корня первого дерева в качестве результирующего корня, вставки этого корня в хорень второго дерева, а затем (рекурсивного) объединения пары левых поддеревьев и пары правых поддеревьев.

private: link joinR(link а, link Ь) {

if (b ~ 0) return a;

if (а 0) return Ь; insertT(Ь, a->item); Ь->1 = joinR(a->l, Ь->1); Ь->г = joinR(a->r, Ь->г) ; delete а; return Ь;

public:

void join(ST<Itern, Key>& b)

{ head = joinR(head, b.head); }

Пример показан на рис. 12.20. Подобно удалению, этот процесс асимметричен и может приводить к деревьям, которые не являются хорошо сбалансированными, однако простое решение проблемы обеспечивает рандомизация, как будет показано в главе 13. Обратите внимание, что в наихудшем случае количество сравнений, использованных для выполнения операции join, должно, по крайней мере, определяться линейной зависимостью; иначе можно было бы разработать алгоритм сортировки, в котором присутствует менее N\gN сравнений, применяя такой подход, как восходящая сортировка слиянием (см. упражнение 12.88).

Мы не включили в программу код, необходимый для поддержки полей счетчика в узлах BST-дерева во время преобразований для операций join и remove, что необходимо в приложениях, где требуется поддерживать также и операцию select (программа 12.14). Концептуально эта задача проста, однако требует определенных усилий. Один из стандартных способов ее выполнения - реализация небольшой вспомогательной процедуры, которая устанавливает значение поля счетчика в узле на единицу больше, чем сумма полей счетчиков в его дочерних узлах, а затем вызов полученной процедуры для каждого узла, связи которого изменяются. В частности, это можно выполнить для обоих узлов в rotL и rotR в программе 12.12, что достаточно для выполнения преобразований в программах 12.13 и 12.15, поскольку они преобразуют деревья исключительно путем ротаций. Для joinLR и removeR в программе 12.16 и join в программе 12.17 достаточно вызвать процедуру обновления счетчика узлов для возвращаемого узла непосредственно перед оператором return.

Базовые операции search, insert и sort для BST-деревьев легко реализовать и выполнить даже при весьма незначительной случайности в последовательности операций, поэтому BST-деревья широко используются применительно к динамическим таблицам символов. Они допускают также простые рекурсивные решения для поддержки других видов операций, как было показано в этой главе на примере операций select, remove и join, и как будет показано во многих примерах далее в книге.

Несмотря на всю полезность, существует два основных недостатка использования BST-деревьев в приложениях. Во-первых, они требуют существенного дополнительного объема памяти для связей. Часто мы считаем, что ссылки и записи имеют практически одинаковые размеры (скажем, одно машинное слово) - если это так, реализация с использованием BST-дерева использует две трети выделенного для нее объема памяти под ссылки и только одну треть под ключи. Данный эффект менее важен в приложениях с большим количеством записей и более важен в средах, в которых указатели велики. Если же память играет первостепенную роль, применению BST-деревьев можно предпочесть один из методов хеширования с открытой адресацией, описанных в главе 14.

Второй недостаток использования BST-деревьев - возможность того, что деревья могут стать плохо сбалансированными и в результате снижать производительность. В главе 13 исследуются еще несколько подходов к обеспечению гарантированной производительности. При наличии достаточного объема памяти под связи, эти алгоритмы делают BST-деревья весьма привлекательными в качестве основы для реализации АТД таблиц символов, поскольку обеспечивают гарантированно высокую производительность для большого набора полезных операций с АТД.

Упражнения

\> 12.78 Реализуйте нерекурсивную функцию BST-дерева (см. программу 12.14).

1> 12.79 Нарисуйте BST-дерево, образованное в результате вставки элементов с ключами Е ASYQUTIONb первоначально пустое дерево и последующего удаления Q.

1> 12.80 Нарисуйте BST-дерево, образованное в результате вставки элементов с ключами Е А S Y в первоначально пустое дерево, вставки элементов с ключами Q U Е S ТI О N в другое первоначально пустое дерево и последующего объединения результатов.

12.81 Реализуйте нерекурсивную функцию remove цдя BST-дерева (см. профамму 12.16).

12.82 Реализуйте версию операции remove для BST-деревьев (профамма 12.16), которая удаляет все узлы дерева, имеющие ключи, равные данному.

о 12.83 Измените реализации таблиц символов, основанные на BST-дереве, чтобы они поддерживали дескрипторы клиентских элементов (см. упражнение 12.7); добавьте реализации деструктора, конструктора копирования и перефуженной операции присваивания (см. упражнение 12.6); добавьте операции remove и Join; воспользуйтесь про-фаммой-драйвером из упражнения 12.22 для проверки своего интерфейса и реализации АТД первого класса таблицы символов.

12.84 Экспериментально определите увеличение высоты BST-дерева при выполнении длинной последовательности чередующихся операций вставки и удаления в произвольном дереве с узлами. N= 10, 100 и 1000, а для каждого значения выполняется до 10 пар вставок-удалений.

12.85 Реализуйте версию функции remove (см. профамму 12.16), которая принимает произвольное решение относительно замены узла, который должен быть удален, узлом-предком или узлом-потомком в дереве. Выполните для этой версии серию экспериментов, описанных в упражнении 12.84.

о 12.86 Реализуйте версию функции remove, которая использует рекурсивную функцию для перемещения узла, который должен быть удален, в нижнюю часть дерева при помощи ротации, подобной вставке в корень (профамма 12.13). Нарисуйте дерево, образованное в результате удаления профаммой корня из полного дерева, состоящего из 31 узла.

о 12.87 Выполните эксперименты для определения увеличения высоты BST-дерева при многократной вставке элемента в корень дерева, образованного в результате объединения поддеревьев корня в произвольном дереве, состоящем из узлов, причем Л = 10, 100 и 1000.

о 12.88 Реализуйте версию восходящей сортировки слиянием, основанной на операции join. Начните с помещения ключей в одноузловых деревьев, затем объедините одно-узловые деревья в пары для получения N/2 двухузловых деревьев, далее объедините двухузловые деревья для получения N/4 четырехузловых деревьев и т.д.

12.89 Реализуйте версию функции join (см. профамму 12.17), которая принимает произвольное решение относительно использования корня первого или корня второго дерева в качестве корня результирующего дерева. Проделайте для этой версии серию экспериментов, описанных в упражнении 12.87.