няющей дерево. Поддержка поля счетчика может не окупаться в некоторых приложениях, в которых основным операциями являются insert и search, но это может оказаться незначительной платой, если важно поддерживать операцию select в динамической таблице символов.

Эту реализацию операции select можно преобразовать в операцию partition (разбиение на части), которая реорганизует дерево для помещения к-то наименьщего элемента в корень, что в точности соответствует рекурсивной технологии, которая использовалась для вставки в корень в разделе 12.8: если мы (рекурсивно) помещаем требуемый узел в корень одного из поддеревьев, его затем можно сделать корнем, всего дерева, применив единственную ротацию. Программа 12.15 содержит реализацию этого метода. Подобно ротациям, разбиение на части не принадлежит к операциям АТД, поскольку эта функция преобразует конкретное представление таблицы символов и не должна быть прозрачной для клиентов. Скорее, это вспомогательная процедура, которую можно использовать для реализации операций АТД либо с целью повыщения эффективности их выполнения. На рис. 12.17 приведен пример, иллюстрирующий аналогично показанному на рис. 12.14, что этот процесс эквивалентен спуску по пути поиска от корня до требуемого узла дерева, а затем подъему обратно с выполнением ротаций для перемещения узла в корень.

Для удаления узла с данным ключом из BST-дерева вначале необходимо проверить, находится ли он в одном из поддеревьев. Если да, мы заменяем это поддерево результатом удаления (рекурсивного) из него узла. Если удаляемый узел находится в корне, дерево заменяется результатом объединения двух поддеревьев в одно. Для выполнения такого объединения существует несколько возможностей. Один из возможных подходов проиллюстрирован на рис. 12.18, а реализация представлена в программе 12.16. Для объединения двух BST-деревьев, все ключи второго из которых заведомо больще ключей первого, ко второму дереву применяется операция partition с целью перемещения в корень наименьшего элемента в этом дереве. На данном этапе левое поддерево корня должно быть пустым (иначе в нем располагался бы элемент, который меньше элемента в корне - явное противоречие), и задачу можно завершить, заменив эту связь связью с первым деревом. На рис. 12.19 показана последовательность удалений в примере дерева, которая иллюстрирует некоторые из возможных ситуаций.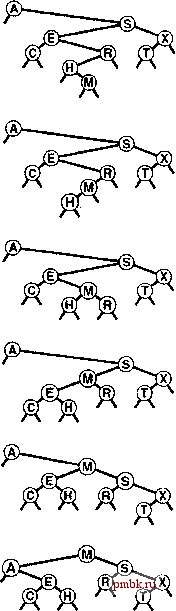

РИСУНОК 12.17 РАЗДЕЛЕНИЕ BST-ДЕРЕВА НА ЧАСТИ

Эта последовательность отображает результат (внизу) разбиения примера BST-дерева (вверху) на части расположенным практически посередине ключом; при этом применяется (рекурсивно) ротация, как это делалось во время вставки в корень.

Программа 12.16 Удаление узла с данным ключом из BST-дерева

В этой реализации операции remove выполняется удаление из BST-дерева первого встреченного узла с ключом v. Выполняя просмотр сверху вниз, программа осуществляет рекурсивные вызовы для соответствующего поддерева до тех пор, пока удаляемый узел не окажется в корне. Затем программа заменяет узел результатом объединения его двух поддеревьев - наименьший узел в правом поддереве становится корнем, а затем его левая связь начинает указывать на левое поддерево.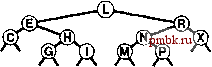

link b)

private: link joinLR(lin* a, {

if (b == 0) return a; partR(b, 0); b->l a; return b;

void removeR(link& h. Key { if (h == 0) return; Key w = h->item.key(); if (v < w) removeR (h->l, (w < v) removeR(h->r, (V = w) link t = h;

h = joinLR(h->l, h->r);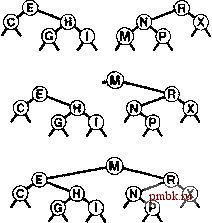

if if {

V) ; V) ;

delete t; }

public: void remove (Item x)

{ removeR{head, x.key());

РИСУНОК 12.18 УДАЛЕНИЕ КОРНЯ В BST-ДЕРЕВЕ

На этой схеме показан результат (внизу) удаления корня из примера BST-дерева (вверху). Вначале мы удаляем узел, оставляя два поддерева (второй сверху рисунок). Затем мы разделяем правое поддерево на части для помещения его наименьшего элемента в корень - (третий сверху рисунок).

Этот подход асимметричен и является особым в од- оставляя левую связь

указывающей на пустое ном отношении: почему в качестве корня нового дере-

ва используется наименьший ключ во втором дереве, а заменяем эту связь связью с

не наибольший ключ в первом дереве? Другими слова- левым поддеревом исходного

ми, почему удаляемый узел заменяется следующим уз- дерева (нижнийрисунок).

лом в поперечном обходе дерева, а не предыдущим.

Можно было бы также рассмотреть другие подходы.

Например, если узел, который должен быть удален, содержит нулевую левую связь, почему бы просто не сделать его правый дочерний узел новым корнем вместо того, чтобы использовать узел с наименьшим ключом в правом поддереве? Предлагались другие, аналогичные, модификации базовой процедуры удаления. К сожалению, всем им присуш один и тот же недостаток: остающееся после удаления дерево не является произвольным, даже если до этого оно было таковым. Более того, было показано, что программа 12.16 склонна оставлять дерево слегка несбалансированным (средняя высота пропорциональна /jV ), если дерево подвергается большому количеству произвольных пар операций удаления-вставки (см. упражнение 12.84).

Упомянутые различия могут быть не заметны в реальных приложениях, если только N не очень велико. Тем не менее подобного рода сочетание элегантного алгорит-

ма с нежелательными характеристиками производительности является неудовлетворительным. В главе 13 будут рассматриваться два различных способа исправления этой ситуации.

Для алгоритмов поиска типично, когда для удаления требуются более сложные реализации, нежели для поиска. Значения ключей играют сложную роль в формировании структуры, поэтому удаление ключа может быть сопряжено со сложными исправлениями. Одна из возможных альтернатив - использование ленивой стратегии удаления, оставляющей удаленные узлы в структуре данных, но помечающей их как удаленные , которые будут игнорироваться при поиске. В реализации поиска в программе 12.8 эту стратегию можно реализовать за счет пропуска проверки на равенство для таких узлов. Необходимо убедиться, что больщие количества помеченных узлов не ведут к из-лищним затратам времени или памяти, но если удаления выполняются не слишком часто, дополнительные затраты могут не играть особой роли. Помеченные узлы можно было бы использовать в будущих вставках, когда это удобно (например, это можно было бы легко сделать для узлов в нижней части дерева). Или же можно было бы периодически перестраивать всю структуру данных, отбрасывая помеченные узлы. Подобные соображения применимы к любой структуре данных, сопряженной с вставками и удалениями, а не только к таблицам символов.

Эта глава завершается рассмотрением реализации операции remove с задействованием дескрипторов и операции join для реализаций АТД таблицы символов, которые используют BST-деревья. Мы предполагаем, что дескрипторы - это ссылки, и опускаем дальнейшие рассуждения на тему формирования пакетов, чтобы можно было сосредоточиться на двух базовых алгоритмах.

Основная сложность в реализации функции для удаления узла с данным дескриптором (связью) та же, что имела место в случае связных списков: необходимо изменить указатель в структуре, который указывает на удаляемый узел. Существует, по меньшей мере, четыре способа решения

упомянутой проблемы. Во-первых, в каждый узел дерева можно добавить третью связь, указывающую на его родительский узел. Недостаток метода заключается в том, что поддерживать дополнительные связи весьма обременительно, как уже отмечалось неоднократно. Во-вторых, можно использовать ключ в элементе для выполнения поиска в дереве, прекращая его после нахождения соответствующего указателя. Недостаток этого подхода в том, что усредненная позиция узла находится в нижней части дерева и, следовательно, этот подход сопряжен с необязательным перемещением по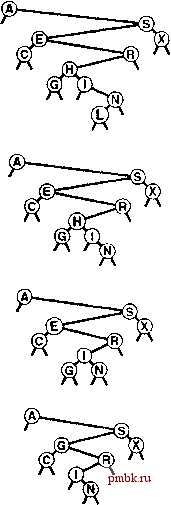

РИСУНОК 12.19 УДАЛЕНИЕ УЗЛА ИЗ BST-ДЕРЕВА

Эта последовательность отображает результат удаления узлов с ключами L, Н и Е из BST-дерева, показанного на верхнем рисунке. Вначале L просто удаляется, поскольку он расположен внизу. Затем Н заменяется на его правый дочерний узел I, поскольку левый дочерний узел I пуст. Наконец, Е заменяется своим потомком G.