На рис. 12.15 и 12.16 показано создание BST-дерева путем вставки последовательности ключей в первоначально пустое дерево с использованием метода вставки в корень. Если последовательность ключей произвольна, построенное таким образом BST-дерево обладает совершенно теми же стохастическими свойствами, что BST-дерево, построенное стандартным методом. Например, леммы 12.6 и 12.7 справедливы и для BST-деревьев, построенных при помощи вставки в корень.

На практике преимущество метода вставки в корень состоит в том, что недавно вставленные ключи располагаются вблизи вершины. Следовательно, затраты на обнаружение попаданий при поиске недавно вставленных ключей, скорее всего, будут ниже, нежели при стандартном методе. Это важно, поскольку во многих приложениях выполняется именно такой динамический набор операций search и insert. Таблица символов может содержать изрядное количество элементов, но значительная часть поисков может относится к наиболее недавно вставленным элементам. Например, в системе обработки коммерческих транзакций активные транзакции могут оставаться вблизи вершины и обрабатываться быстро без обращения к старым транзакциям, которые должны быть опущены. Метод вставки в корень автоматически придает структуре данных это и аналогичные свойства.

Если также изменить функцию search, чтобы она помещала найденный узел в корень, получится метод самоорганизующегося поиска (см. упражнение 12.28), который сохраняет часто посещаемые узлы вблизи вершины дерева. В главе 13 будет показано систематичное применение этой иди при создании реализации таблицы символов, обладающей гарантированными характеристиками производительности.

Как и в случае ряда других методов, упомянутых в этой главе, трудно точно определить производительность метода вставки в корень по сравнению со стандартным методом вставки, поскольку производительность настолько зависит от комбинации различных операций с таблицей символов, что ее трудно проанализировать аналитически. Невозможность проанализировать алгоритм не обязательно должна удерживать от использования вставки в корень, когда известно, что основная масса поисков будет связана с недавно вставленными данными, однако всегда требуются гарантии в отношении производительности; основной темой в главе 13 являются такие методы конструирования BST-деревьев, которые могут предоставить такие гарантии.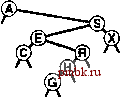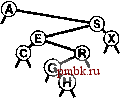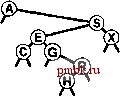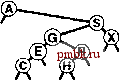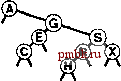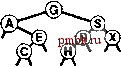

РИСУНОК 12.14 ВСТАВКА В КОРЕНЬ BST-ДЕРЕВА

Эта последовательность отображает результат вставки G в BST-дерево, приведенное на верхнем рисунке, после (рекурсивного) выполнения ротации после вставки с целью перемещения вставленного узла G в корень. Этот процесс эквивалентен вставке G с последующим выполнением последовательности ротаций для перемещения его в корень.

Упражнения

> 12.73 Нарисуйте BST-дерево, образующееся при вставке элементов с ключами EASYQUESTIONb первоначально пустое дерево методом вставки в корень.

12.74 Приведите последовательность из 10 ключей (используя буквы от А до J), для которой при вставке в первоначально пустое дерево методом вставки в корень для создания дерева требуется максимальное количество сравнений. Укажите количество используемых сравнений.

12.75 Добавьте код, необходимый, чтобы программа 12.12 корректно изменяла поля счетчиков, которые должны изменяться после ротации.

о 12.76 Реализуйте нерекурсивную функцию вставки в корень BST-дерева (см. программу 12.13).

12.77 Эмпирически определите среднее значение и стандартное отклонение количества сравнений, используемых для обнаружения попаданий и промахов при поиске в BST-дереве, построенном при помощи вставки произвольных ключей в первоначально пустое дерево и последующего выполнения Л произвольных поисков /V/10 наиболее недавно вставленных ключей для N = 10 10 10 и 10. Проделайте эксперименты и для стандартного метода вставки и для метода вставки в корень; затем сравните полученные результаты.

12.9 Реализации других функций с помощью BST-дерева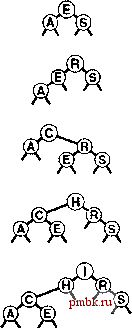

РИСУНОК 12.15 СОЗДАНИЕ BST-ДЕРЕВА ЗА СЧЕТ ВСТАВКИ В КОРЕНЬ

Эта последовательность отображает результат вставки ключей А S Е R С HI в первоначси1ьно пустое BST-дерево при помощи метода вставки в корень. Каждый новый узел вставляется в корень с изменением связей, расположенных вдоль его пути поиска, что приводит к образованию соответствующего BST-дерева.

Рекурсивные реализации, приведенные в разделе 12.5 для основных функций search, insert и sort, которые используют структуры бинарных деревьев, достаточно просты. В этом разделе рассматриваются реализации функций select, join и remove. Одна из них, select, имеет также рекурсивную реализацию, однако реализация других может оказаться трудной

задачей, приводящей к проблемам, связанным с производительностью. Операцию select важно рассмотреть, поскольку возможность эффективной поддержки операций select и sort - одна из причин, по которой для многих приложений BST-деревья оказываются предпочтительнее других структур. Некоторые программисты избегают использования BST-деревьев, чтобы не иметь дело с операцией remove; в этом разделе рассматривается компактная реализация, которая связывает эти операции вместе и использует технологию ротации к корню, описанную в разделе 12.8.

В общем случае операции связаны с перемещением вниз по дереву; поэтому для случая произвольного BST-дерева можно ожидать, что затраты будут определяться логарифмической зависимостью. Однако, нельзя гарантировать, что BST-деревья останутся произвольными после выполнения над ними нескольких операций. В конце этого раздела мы вернемся к данному вопросу.

Для реализации операции select можно использовать рекурсивную процедуру, аналогичную методу выбора с использованием быстрой сортировки, который описан в разделе 7.8. Для отыскания в BST-дереве элемента с к-м наименьшим ключом проверяется количество узлов в левом поддереве. Если там имеется к узлов, возвращается корневой элемент. В противном случае, если левое поддерево содержит более к узлов, отыскивается (рекурсивно) -й наименьший узел в нем. Если ни одно из этих условий не соблюдается, то левое поддерево содержит t элементов при t < к, ]л. к-й наименьший элемент в BST-дереве является {k - t- 1)-м наименьшим элементом в правом поддереве. Программа 12.14 содержит реализацию описанного метода. Как обычно, поскольку каждое выполнение функции завершается максимум одним рекурсивным вызовом, нерекурсивная версия очевидна (см упражнение 12.78).

Программа 12.14 Выбор с помощью BST-дерева

В этой процедуре предполагается, что размер поддерева поддерживается для каждого узла дерева. Сравните эту программу с выбором с использованием быстрой сортировки в массиве (программа 9.6).

private: Item selectR(link h, int к)

{ if (h == 0) return nullltem;

int t = (h->l = 0) ? 0: h->l->N; if (t > k) return selectR(h->l, k); if (t < k) return aelectR(h->r, k-t-1); return h->item;

public: Item select <int k)

{ return selectR(head, k); }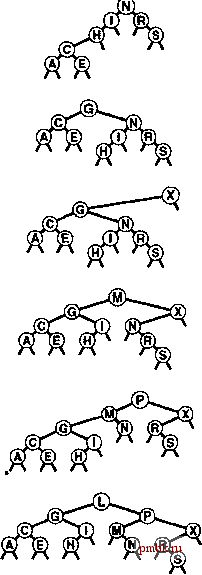

РИСУНОК 12.16 КОНСТРУИРОВАНИЕ BST-ДЕРЕВА ПРИ ПОМОЩИ ВСТАВКИ В КОРЕНЬ (ПРОДОЛЖЕНИЕ) Эта последовательность отображает вставку ключей N GXMPLe BST-дерево, которое начинало создаваться на рис. 12.15.

С точки зрения алгоритма основная причина включения полей счетчика в узлы BST-дерева - необходимость поддержки реализации операции select. Это позволяет также обеспечивать тривиальную реализацию операции count (возвращение поля счетчика в коневом узле); в главе 13 будет продемонстрировано еще одно применение. Недостатки присутствия поля счетчика заключаются в использовании дополнительной памяти для каждого узла и необходимости обновления поля каждой функцией, изме-