Таблица 12.2 Эмпирические исследования реализаций таблиц символов

В этой таблице приведено относительное время создания таблицы символов и поиска каждого ключа в таблице. Деревья бинарного поиска обеспечивают быстрые реализации поиска и вставки; при использовании всех других методов для выполнения одной из этих двух задач требуется время, определяемое квадратичной зависимостью. В общем случае бинарный поиск выполняется несколько быстрее поиска в BST-дереве, но он не может быть использован применительно к очень большим файлам, если только таблицу нельзя предварительно отсортировать. Стандартная реализация BST-дерева распределяет память для каждого узла дерева, в то время как реализация с использованием индексов предварительно распределяет память для всего дерева (что ускоряет создание) и вместо указателей использует индексы массивов (что замедляет поиск).

Ключ: А В С Т

Неупорядоченный массив (упражнение 12.20) Упорядоченный связный список (упражнение 12.21) Бинарный поиск (программа 12,7)

Дерево бинарного поиска, стандартное (программа 12.8) Индексированное дерево бинарного поиска (упражнение 12.67)

12.8 Вставка в корень в деревьях бинарного поиска

в стандартной реализации BST-деревьев каждый новый вставленный узел попадает куда-то в нижнюю часть дерева, заменяя какой-то внешний узел. Это не является абсолютно обязательным; это всего лишь следствие естественного алгоритма с использованием рекурсивной вставки. В этом разделе рассматривается другой метод вставки, при котором каждый новый элемент вставляется в корень, и поэтому недавно вставленные узлы находятся вблизи вершины дерева.

Построенные таким образом деревья обладают рядом интересных свойств, но главная побудительная причина рассмотрения этого метода в том, что он играет важную роль в двух из усовершенствованных алгоритмов, рассматриваемых в главе 13.

Предположим, что ключ вставляемого элемента больше ключа в корне. Создание нового дерева можно было бы начать с помещения нового элемента в новый корневой

узел, устанавливая старый корень в качестве левого поддерева, а правое поддерево старого корня в качестве правого поддерева. Однако, правое поддерево может содержать некоторые меньшие ключи, поэтому для завершения вставки потребуется выполнить дополнительные действия. Аналогично, если ключ вставляемого элемента меньше ключа корня и больше всех ключей в левом поддереве корня, можно снова создать новое дерево с новым элементом, помешенным в корне, но если левое поддерево содержит какие-либо большие ключи, необходимы дополнительные действия. Пе-ремешения всех узлов с меньшими ключами в левое поддерево и всех узлов с большими ключами в правое в обшем случае оказывается сложным преобразованием, поскольку узлы, которые должны быть перемешены, могут быть разбросаны по всему пути поиска для вставляемого узла.

К счастью, сушествует простое рекурсивное решение этой проблемы, которое основывается на ротации (rotation) - фундаментальном преобразовании деревьев. По сушеству, ротация позволяет менять местами роль корня и одного из его дочерних узлов при сохранении порядка ключей в узлах BST-дерева. Ротация вправо затрагивает корень и левый дочерний узел (см. рис. 12.12). Ротация помешает корень справа, изменяя на обратное направление левой связи корня: перед ротацией она указывает от корня к левому дочернему узлу, а после ротации - от левого дочернего узла (нового корня) к старому корню (правый дочерний узел нового корня). Основная часть, которая обеспечивает работу ротации, - копирование правой связи левого дочернего узла, чтобы она стала левой связью старого корня. Эта связь указывает на все узлы с ключами между двумя узлами, участвующими в ротации. И наконец, связь со старым корнем должна быть изменена так, чтобы указывать на новый корень. Описание ротации влева аналогично приведенному выше, с учетом замены оп-редлений правый и левый (см. рис. 12.13).

Ротация - это локальное изменение, затрагивающее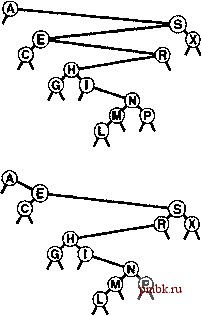

РИСУНОК 12.12 РОТАЦИЯ ВПРАВО В BST-ДЕРЕВЕ

Иа этой схеме показан результат (внизу) ротации вправо в узле S в примере BST-дерева (вверху). Узел, содержащий S, перемещается в дереве вниз, становясь правым дочерним узлом своего прежнего левого дочернего узла.

Ротация выполняется путем получения связи с новым корнем Е из левой связи S, установки левой связи S путем копирования правой связи Е, установки правой связи Е указывающей на Su установки связи из А указывающей не на S, а на Е. Эффект ротации заключается в перемещении Е и его левого поддерева на один уровень вверх и перемещение S и его правого поддерева на один уровень вниз. Остальная часть дерева остается неизменной.

ТОЛЬКО три связи и два узла, которое позволяет перемещать узлы по деревьям, не изменяя глобальные свойства порядка, превращающие BST-дерево в полезную структуру для поиска (см. программу 12.12). Ротации используются для перемещения конкретных узлов по дереву и для предотвращения разба-лансировки деревьев. В разделе 12.9 с помощью ротаций реализованы remove, join и

другие операции с АТД; в главе 13 они будут применяться для построения деревьев, для которых допустима неоптимальная производительность.

Программа 12.12 Ротации в BST-деревьях

Эти две симметричных процедуры выполняют операцию rotation (ротация) в BST-дереве. Ротация вправо делает старый корень правым поддеревом нового корня (старого левого поддерева корня); ротация влево превращает старый корень в левое поддерево нового корня (старого правого поддерева корня). Для реализаций, в которых поле счетчика поддерживается в узлах (например, для поддержки операции select, как будет показано в разделе 14.9), необходимо также обменять поля счетчиков для участвующих в ротации узлах (см. упражнение 12.75).

void rotR(link& h)

{ link X = h->l; h->l = x->r; x->r = h;

h = x; } void rotL(link& h)

{ link X = h->r; h->r = x->l; x->l = h;

h = x; }

Операции ротации обеспечивают простую рекурсивную реализацию вставки в корень: необходимо рекурсивно вставить новый элемент в соответствующее поддерево (оставив его по заверщении рекурсивной операции в корне этого дерева), а затем выполнить ротацию, чтобы сделать узел корнем главного дерева. Пример показан на рис. 12.14, а программа 12.13 содержит реализацию данного метода. Эта программа - убедительный пример больших возможностей рекурсии. Любой читатель, которого это не убеждает, может попытаться выполнить упражнение 12.76.

Программа 12.13 Вставка в корень BST-дерева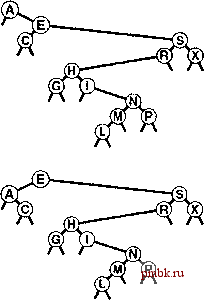

РИСУНОК 12.13 РОТАЦИЯ ВЛЕВО В BST-ДЕРЕВЕ

На этой схеме показан результат (внизу) ротации влево узла А в примере BST-дерева (вверху). Узел, содержащий А, перемещается вниз, становясь левым дочерним узлом своего прежнего правого дочернего узла.

Ротация выполняется за счет получения связи с новым корне.м Е из правой связи А, установки правой связи А путем копирования левой связи Е, установки левой связи Е на А и установки связи с А (верхняя связь дерева) вместо этого на Е.

При наличии функций ротации, определенных в программе 12.12, реализация рекурсивной функции, которая вставляет новый узел в корень BST-дерева, очевидна: необходимо вставить новый элемент в корень соответствующего поддерева, а затем выполнить соответствующую ротацию, что приведет к его переносу в корень главного дерева.

private: void insertT (linkfi h, Item x)

{ if (h == 0) { h = new node(x); return; } if (x.keyO < h->item.key 0)

{ insertT(h->l, x); rotR(h) ; } else { insertT(h->r, x) ; rotL(h); }

public: void insert(Item item) { insertT(head, item); }