12.64 Определите эмпирически среднее и стандартное отклонение количества сравнений, использованных для обнаружения попаданий и промахов при поиске в BST-дереве, созданном в результате вставки 7V произвольных ключей в первоначально пустое дерево, для = 10 10 *, 10 и 10.

12.65 Создайте программу, которая строит / BST-деревьев за счет вставки произвольных ключей в первоначально пустое дерево и вычисляет максимальную высоту дерева (максимальное количество сравнений, необходимых для обнаружения любого промаха при вставке в любом из / деревьев) для N= 10 10 *, 10 и 10* при /= 10, 100 и 1000.

12.7 Реализация индексов при использовании таблиц символов

Во многих приложениях необходимо выполнять поиск в структуре просто с целью нахождения элементов без их перемещения. Например, может существовать массив элементов с ключами, для которого требуется метод поиска, определяющий в массиве индекс элемента, соответствующего определенному ключу. Может также требоваться удаление элемента с данным индексом из структуры поиска с его сохранением в массиве для какого-либо другого применения. В разделе 9.6 были рассмотрены преимущества обработки индексированных элементов в очередях по приоритету, которые косвенно обращаются к данным клиентского массива. Применительно к таблицам символов эта же концепция ведет к уже знакомым индексам: внещней по отнощению к набору элементов поисковой структуры, которая обеспечивает быстрый доступ к элементам с данным ключом. В главе 16 будет рассматриваться случай, когда элементы и, возможно, даже индексы хранятся во внещнем хранилище; в этом разделе кратко исследуется случай, когда и элементы и индексы размещаются в памяти.

Деревья бинарного поиска можно определить таким образом, чтобы индексы строились в точности так же, как при обеспечении косвенного метода для сортировки в разделе 6.8 и для сортирующих деревьев в разделе 9.6: необходимо использовать контейнер Index для определения элементов BST-дерева и обеспечить, чтобы ключи извлекались из элементов, как обычно, через функцию-члена key. Более того, для связей можно использовать параллельные массивы, как это было сделано для связных списков в главе 3. Используются три массива: для элементов, левых связей и правых связей. Связи являются индексами массивов (целыми значениями) и ссылки на связи, подобные

X = х->1

во всем коде заменяются на ссылки типа

X = 1[х]

Этот подход устраняет затраты на динамическое распределение памяти для каждого узла - элементы занимают массив независимо от функции поиска, и мы заранее вьщеляем два целочисленных значения на каждый элемент для хранения связей дерева, признавая, что потребуется объем памяти не меньще этого, когда все элементы будут помещены в структуру поиска. Память под связи используется не всегда, тем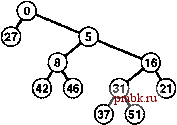

не менее, она всегда готова для использования подпрограммой поиска, не требуя дополнительного времени на распределение. Другая важная особенность этого подхода заключается в том, что он допускает добавление дополнительных массивов (содержащих дополнительную связанную с каждым узлом информацию) без какого-либо изменения кода манипулирования деревом. Когда подпрограмма поиска возвращает индекс элемента, она предоставляет способ немедленного доступа ко всей информации, связанной с этим элементом, путем использования индекса для доступа к соответствующему массиву.

Такой способ реализации BST-деревьев как средства упрощения поиска в больщих массивах элементов иногда весьма полезен, поскольку исключает дополнительные затраты на копирование элементов во внутреннее представление АТД и перегрузки, связанной с распределением и конструированием при помощи new. Использование массивов не подходит, когда объем памяти играет первостепенную роль, а таблица символов увеличивается и уменьщается в значительных пределах. В особенности это актуально, если заранее трудно предвидеть максимальный размер таблицы символов. Если невозможно точно предвидеть размер, неиспользуемые связи могут привести к напрасному расходованию памяти в области массива элементов.

Важное применение концепции индексирования - обеспечение поиска ключевых слов в строке текста (см. рис. 12.11). В программе 12.11 показан пример такого приложения. Она считывает текстовую строку из внешнего файла. Затем, просматривая каждую позицию в текстовой строке с целью определения ключа строки от данной позиции и до конца строки, она вставляет все ключи в таблицу символов, используя указатели на строки. Подобное применение ключей строк отличается от определения типа строкового элемента, как в упражнении 12.2, поскольку никакое распределение памяти под область хранения не требуется. Использованные ключи строк имеют произвольную длину, но мы поддерживаем только указатели на них и просматриваем лишь то количество символов, которое требуется для определения того, какая из двух строк должна следовать первой. Никакие две строки не совпадают (например, все они имеют различную длину), но если изменить операцию ==, чтобы сравнить при условии, что одна является префиксом второй, можно было бы воспользоваться таб-

0 call me isbmael some...

5 me ishmael some year...

8 ishmael some years a.,. 16 some years ago never... 21 years ago never mind... 27 ago never mind how 1... 31 never mind how long.,. 37 mind how long precis... 42 how long precisely h,., 46 long precisely havin... 51 precisely having lit...

РИСУНОК 12.11 ИНДЕКС ТЕКСТОВОЙ СТРОКИ

В этом примере индекса строки мы определяем ключ строки так, чтобы он начинался с каждого слова в тексте; затем строится BST-дерево за счет обращения к ключам по их индексам строк. В принципе, ключи имеют произвольную длину, но в общем случае исследуются только несколько начальных символов. Например, для определения того, встречается ли фраза never mind в этом тексте, она сравнивается с call... в корне (индекс строки 0), затем с те... в правом дочернем узле корня (индекс 5), затем с some... в правом дочернем узле этого узла (индекс 16), а затем never mind отыскивается в левом дочернем узле данного узла (индекс 31).

лицей символов для выяснения того, присутствует ли данная строка в тексте, и простым вызовом функции search.

Программа 12.11 Пример индексирования текаовых строк

В этой программе предполагается, что item.cxx определяет представление данных char* для ключей строк в элементах, перегруженную операцию operator<, которая использует strcmp, перегруженную операцию operator==, которая использует strncmp и оператор преобразования из Item в char* {см. текст). Главная программа считывает текстовую строку из указанного файла и использует таблицу символов для построения индекса из строк, определяемых начальными символами текстовых строк. Затем она считывает запрашиваемые строки из стандартного ввода и выводит позицию, в которой запрос найден в тексте (или выводит строку not found). При реализации таблицы символов с использованием BST-дерева поиск выполняется быстро даже для очень больших строк.

#iiiclude <iostream.h> tinclude <fstreain.h> finclude Item.cxx #include ST.cxx static char text[maxN]; int main(int argc, char *argv[]) { int N = 0; char t; ifstream corpus; corpus.open(*++argv); while (N < maxN && corpus .get (t)) text[N++] = t; text[N] = 0; ST<Item, Key> st(maxN) ;

for (int i = 0; i < N; i++) st. insert (Stext [i]) ; char query [maxQ]; Item x, v(query) ; while (cin.getline(query, maxQ))

if ((X = st.search(v.key())) .nullO)

cout not found: query endl;

else cout x-text : query endl;

Программа 12.11 считывает серии запросов со стандартного ввода, использует функцию search для определения присутствия каждого запроса в тексте и выводит позицию в тексте для первого совпадения с запросом. Если таблица символов реализована с использованием BST-дерева, то в соответствие с леммой 12.6 можно ожидать, что для поиска потребуется около 2N \r\N сравнений. Например, как только индексы построены, любую фразу в тексте, состоящем приблизительно из 1 миллиона символов, можно было бы найти с использованием около 30 операций сравнения строк. Это приложение равносильно индексированию, поскольку указатели строк С являются индексами массива символов: если х указывает на text[i], то разность двух указателей, x-text, равна i.

При построении индексов в реальных приложениях потребуется учесть и множество других моментов. Существует множество способов, в соответствие с которыми можно извлечь конкретные преимущества из свойств ключей строк в плане ускорения работы алгоритмов. Более сложные методы поиска строк и создания индексов с полезными возможностями ключей строк будут основными темами в части 5.

В таблицу 12.2 сведены результаты исследований, подтверждающие приведенные аналитические рассуждения и демонстрирующие применение деревьев бинарного поиска для работы с динамическими таблицами символов с произвольными ключами.