извольных ключах, потому-то в среднем деревья достаточно хорошо сбалансированы. В этом разделе мы детализируем это наблюдение.

В частности, длина пути и высота бинарных деревьев, рассмотренные в разделе 5.5, непосредственно связаны с затратами на поиск в BST-деревьях. Высота определяет стоимость поиска в худшем случае, длина внутреннего пути непосредственно связана со стоимостью попаданий при поиске, а длина внешнего пути непосредственно связана со стоимостью промахов при поиске.

Лемма 12.6 Для обнаружения попадания при поиске в дереве бинарного поиска, образованном N произвольными ключами, в среднем требуется около 2 IgN- 1.39 \gN сравнений.

Как упоминалось в разделе 12.3, мы считаем последовательные операции == и < одной операцией сравнения. Количество сравнений, использованных для обнаружения попадания при поиске, завершающемся в данном узле, равно 1 плюс расстояние от этого узла до корня. Таким образом, интересующая величина равна 1 плюс средняя длина внутреннего пути BST-дерева, которую можно проанализировать с использованием уже знакомых рассуждений: если Сд - средняя длина внутреннего пути BST-дерева, состоящего из N узлов, мы имеем следующее рекуррентное соотношение:

Cj, = N-l + ~ (Ck-,+CN-k),

\<k<N

при Ci = 1. Член N- 1 учитывает, что корень увеличивает длину пути для каждого из остальных N- 1 узлов на 1; остальная часть выражения вытекает из того, что ключ в корне (вставленный первым) с равной вероятностью может быть к-м по величине ключом, разбивая дерево на произвольные поддеревья размерами А: - 1 и N - к. Это рекуррентное соотношение почти идентично тому, которое решалось в главе 7 для метода быстрой сортировки, и для получения оговоренного результата его можно решить так же.

Лемма 12.7 Для выполнения вставок и обнаружения промахов при поиске в дереве бинарного поиска, образованном N произвольными ключами, в среднем требуется около 2 IgN ~ 1.39 IgA сравнений.

Поиск произвольного ключа в дереве, содержащем узлов, с равной вероятностью может завершиться в любом из Л- 1 внешних узлов обнаружением промаха при поиске. Эта лемма в сочетании с тем, что разница длин внешнего и внутрен-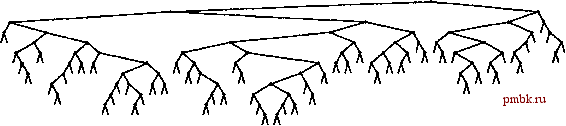

РИСУНОК 12.8 ПРИМЕР ДЕРЕВА БИНАРНОГО ПОИСКА

В этом BST-дереве, которое было построено за счет вставки около 200 произвольных ключей в первоначально пустое дерево, ни один поиск не использует более 12 сравнений. Средняя стоимость обнаружения попадания при поиске приблизительно равна 10.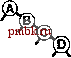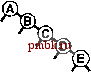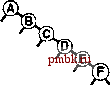

него пути в любом дереве равна просто 2 N (см. лемму 5.7), обусловливает оговоренный результат. В любом BST-дереве среднее количество сравнений, необходимых для выполнения вставки или обнаружения промаха, приблизительно на 1 больше среднего количества сравнений, необходимых для выявления попадания при поиске.

В соответствии с леммой 12.6 следует ожидать, что затраты на поиск для BST-деревьев должна быть приблизительно на 39% выше затрат для бинарного поиска произвольных ключей. Но в соответствии с леммой 12.7 дополнительные затраты вполне окупаются, поскольку новый ключ может быть вставлен почти при тех же затратах - подобная гибкость при использовании бинарного поиска не доступна. На рис. 12.8 показано BST-дерево, полученное в результате длинной цепи произвольных перестановок. Хотя оно содержит несколько длинных и несколько коротких путей, его можно считать хорошо сбалансированным: для выполнения любого поиска требуется менее 12 сравнений, а среднее количество сравнений, необходимых для обнаружения произвольного попадания при поиске равно 7.00, что сравнимо с 5.74 для случая бинарного поиска.

Леммы 12.6 и 12.7 определяют производительность для среднего случая при условии, что порядок ключей произволен. Если это не так, производительность алгоритма имеет тенденцию к снижению.

Лемма 12.8 В худшем случае для поиска в дереве бинарного поиска с N ключами может требоваться N сравнений. На рис. 12.9 и 12.10 показаны два примера наихудших случаев BST-деревьев. Для этих деревьев поиск с использованием бинарного дерева ничем не лучше последовательного поиска с использованием односвязных списков.

Таким образом, высокая производительность базовой реализации таблиц символов с использованием BST-дерева требует, чтобы ключи в достаточной степени были подобны произвольным ключам, а дерево не содержало длинных путей. Более того, наихудший случай не столь уж редко встречается на практике - он возникает при вставке ключей в первоначально пустое дерево по порядку или в обратном порядке с применением стандартного алгоритма - последовательность операций, которую мы определено можем предпринять, не получив никакого явного предупреждения не делать этого. В главе 13 исследуются технологии превращения этого худшего случая в крайне маловероятный и полного его исключения, превращения всех деревьев в подобные деревьям для наилучшего случая, длины всех путей в которых гарантировано определяются логарифмической зависимостью.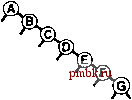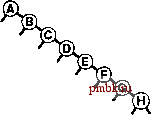

РИСУНОК 12.9 ХУДШИЙ СЛУЧАЙ ДЕРЕВА БИНАРНОГО ПОИСКА

Если ключи в BST-дереве вставляются в порядке возрастания, дерево вырождается в форму, эквивалентную односвязному списку, приводя к квадратичной зависимости времени создания дерева и к линейной зависимости времени поиска.

Ни одна из других рассмотренных реализаций таблиц символов не может использоваться для выполнения задачи вставки в таблицу очень большого количества произвольных ключей, а затем поиска каждого из них - время выполнения каждого из методов, описанных в разделах 12.2- 2.4 определяется квадратичной зависимостью. Более того, из анализа следует, что среднее расстояние до узла в бинарном дереве пропорционально логарифму количества узлов в дереве, что позволяет эффективно выполнять смешанные наборы операций поиска, вставки и других операций с АТД таблицы символов, что и будет вскоре показано.

Упражнения

t> 12.56 Создайте рекурсивную профамму, которая вычисляет максимальное количество сравнений, требуемых для любого поиска в данном BST-дереве (высоту дерева).

t> 12.57 Создайте рекурсивную программу, которая вычисляет максимальное количество сравнений, требуемых для попадания при поиске в данном BST-дереве (длину внутреннего пути дерева, деленную на n).

12.58 Приведите последовательность вставок ключей Е А SYQUESTIONb первоначально пустое BST-дерево, чтобы созданное при этом дерево было эквивалентно бинарному поиску в смысле последовательности сравнений, выполняемых при поиске любого ключа в BST-дереве и при бинарном поиске.

о 12.59 Создайте программу, которая вставляет набор ключей в первоначально пустое BST-дерево так, чтобы созданное дерево было эквивалентно бинарному поиску, как описывалось в упражнении 12.58.

12.60 Нарисуйте все различающиеся по структуре BST-деревья, образованные после вставки Л ключей в первоначально пустое дерево, для 2 < N < 5.

12.61 Определите вероятность того, что каждое из деревьев в упражнении 12.60 является результатом вставки Л произвольных различных элементов в первоначально пустое дерево.

12.62 Сколько бинарных деревьев, состоящих из узлов, имеют высоту 7V? Сколько существует различных способов вставки различных ключей в первоначально пустое дерево, приводящих к образованию BST-дерева с высотой Л?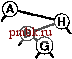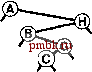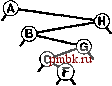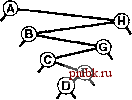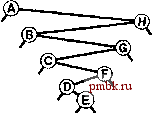

®

РИСУНОК 12.10 ЕЩЕ ОДИН ХУДШИЙ СЛУЧАЙ ДЕРЕВА БИНАРНОГО ПОИСКА

Множество других подобных вариантов порядка вставки ключей приводят к вырождению BST-дерева. Тем не менее, дерево бинарного поиска, образованное произвольно упорядоченными ключами, скорее всего, окажется хорошо сбалансированным.

о 12.63 Докажите с использованием метода индукции, что разница между длинами внешнего и внутреннуго путей в любом бинарном дереве составляет 2jV(cm. лемму 5.7).