Как упоминалось в разделе 12.1, периодически, в случае необходимости систематического посещения каждого из элементов таблицы символов, мы будем обращаться к общей операции visit для таблиц символов. Применительно к BST-деревьям можно посетить элементы в порядке следования их ключей, заменив в только что приведенном описании операцию show операцией visit и, возможно, обеспечив передачу в функцию посещения элемента в качестве параметра (см. раздел 5.6).

Нерекурсивный подход при обдумывании реализации поиска и вставки в BST-деревьях несомненно представляет интерес. При нерекусивной реализации процесс поиска состоит из цикла, в котором искомый ключ сравнивается с ключом в корне, затем выполняется перемещение влево, если оюч поиска меньше, и вправо - если он больше ключа в корне. Вставка состоит из обнаружения промаха при поиске (завершающегося на пустой связи) и последующей замены пустой связи указателем на новый узел. Этот процесс соответствует явному манипулированию связями, расположенными вдоль пути вниз по дереву (см. рис. 12.4). В частности, чтобы иметь возможность вставить новый узел в нижней части дерева, необходимо сохранять связь, с родительским узлом текущего узла, как имеет место в реализации в программе 12.10. Как обычно, рекурсивная и нерекурсивная версии, по существу, эквивалентны, причем понимание обоих подходов способствует углублению наших представлений об алгоритмах и структурах данных.

Программа 12.10 Вставка в BST-дерево (нерекурсивная)

Вставка элемента в BST-дерево эквивалентна выполнению неуспешного поиска этого элемента и последующего присоединения нового узла элемента вместо нулевой связи в месте завершения поиска. Присоединение нового узла требует отслеживания родительского узла р текущего узла q в процессе перемещения вниз по дереву. При достижении нижней части дерева р указывает на узел, связь которого необходимо изменить так, чтобы она указывала на новый вставленный узел.

void insert(Item х) { Key V = x.key О ; if (head == 0)

{ head = new node(x); return; } link p = head;

for (link q = p; q !=0; P = q?q : p) q = (v < q->item.key 0) ? q->l : q->r;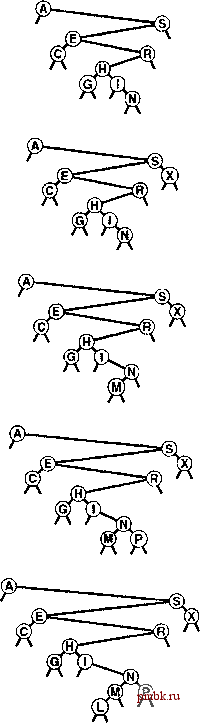

РИСУНОК 12.6 СОЗДАНИЕ ДЕРЕВА БИНАРНОГО ПОИСКА (ПРОДОЛЖЕНИЕ)

Эта последовательность отражает вставку ключей GXMPLe BST-дерево, создание которого было показано на рис. 12.5.

if (v < p->item.key О) р->1 = new node(х);

else p->r = new node (x) ;

Функции BST-дерева в профамме 12.8 не проверяют явно наличие элементов с дублированными ключами. При вставке нового узла, ключ которого равен какому-либо ключу, уже вставленному в дерево, узел помещается справа от присутствующего в дереве узла. Одним из побочных эффектов подобного соглащения является тр, что узлы с дублированными ключами не отображаются в дереве последовательно (см. рис. \2J)i Однако, их можно найти, продолжив поиск с точки, в которой функция search находит первое совпадение, пока не встретится связь 0. Как упоминается в разделе 9.1, существует несколько других возможностей обработки элементов с одинаковыми ключами.

Деревья бинарного поиска - аналог быстрой сортировки. Узел в корне дерева соответствует разделяющему элементу при быстрой сортировке (никакие ключи слева от него не могут быть больще, и никакие ключи справа не могут быть меньше него). В разделе 12.6 будет показано, как это наблюдение связано с анализом свойств деревьев.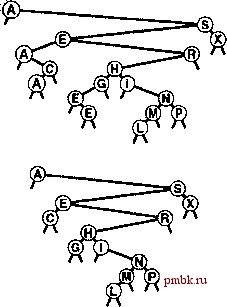

РИСУНОК 12.7 ДУБЛИРОВАННЫЕ КЛЮЧИ В ДЕРЕВЬЯХ БИНАРНОГО ПОИСКА

Когда BST-дерево содержит записи с дублированными ключами (вверху), они оксЛываются разбросанными по всему дереву, что иллюстрируется выделенными узлами А. Все дублированные ключи размещаются вдоль пути поиска ключа от корня до внешнего узла, и поэтому они легкодоступны. Однако, во избежание путаницы при использовании, типа А Упражнения располагается под С , в примерах

О 12.46 Нарисуйте BST-дерево, образующееся при спьэуются различные ключи вставке элементов с ключами EASYQUTIO (* .)/-N в первоначально пустое дерево.

> 12.47 Нарисуйте BST-дерево, образующееся при вставке элементов с ключами Е ASYQUESTIONb первоначально пустое дерево.

> 12.48 Укажите количество сравнений, необходимых для помещения ключей Е А S YQUESTIONb первоначально пустую таблицу символов за счет использования BST-дерева Считайте, что операция search выполняется для каждого ключа, вслед за чем выполняется операция insert для каждого промаха при поиске, как имеет место в программе 12.3.

о 12.49 Вставка ключей в порядке ASERHINGCb первоначально пустое дерево также дает верхнюю часть дерева, показанного на рис. 12.6. Приведите десять других вариантов порядка этих ключей, которые обеспечат тот же результат.

12.50 Реализуйте функцию searchinsert для BST-деревьев (программа 12.8). Функция должна искать в таблице символов элемент с таким же ключом, как и у данного элемента, а затем вставлять элемент, если не находит ни одного такого элемента.

> 12.51 Создайте функцию, которая возвращает количество элементов в BST-дереве, имеющих ключ, равный данному.

12.52 Предположите, что заблаговременно известно, насколь часто должно выполняться обращение к ключам поиска в бинарном дереве. Должны ли ключи вставляться в дерево в порядке возрастания или убывания ожидаемой частоты обращения к ним? Обоснуйте ответ.

о 12.53 Упростите код поиска и вставки в реализации BST-дерева программы 12.8, воспользовавшись двумя фиктивными узлами: head, содержащим элемент с зарезервированным ключом, который меньше всех остальных и правая связь которого указывает на корень дерева; и z, содержащим элемент со служебным ключом, который больше всех остальных, и левая и правая связи которого указывает на него самого, причем он представляет все внешние узлы (внешние узлы являются связями с z). (См. табл. 3.1).

12.54 Измените реализацию BST-дерева в программе 12.8 для хранения элементов с дублированными ключами в связных списках, размещенных в узлах дерева. Измените интерфейс, чтобы операция search работала подобно операции sort (для всех элементов с ключом поиска).

12.55 В нерекурсивной процедуре вставки в профамме 12.10 для определения того, какую связь узла р необходимо заменить новым узлом, используется избыточное сравнение. Приведите реализацию, в которой для исключения этого сравнения используются указатели на связи.

12.6 Характериаики производительноаи деревьев бинарного поиска

время выполнения алгоритмов обработки BST-деревьев зависит от форм деревьев. В лучшем случае дерево может быть полностью сбалансированным и содержать приблизительно IgTV узлов между корнем и каждым из внешних узлов, но в худшем случае в каждый из путей поиска может содержать N узлов.

Можно также надеяться, что в среднем время поиска также будет связано с количеством узлов логарифмической зависимостью, поскольку первый вставляемый элемент становится корнем дерева. Если N ключей должны быть вставлены в произвольном порядке, то этот элемент делил бы ключи пополам (в среднем), что дало бы логарифмическую зависимость времени поиска (при использовании аналогичных рассуждений применительно к поддеревьям). Действительно, возможен случай, когда BST-дерево приводит в точности к тем же сравнениям, что и бинарный поиск (см. упражнение 12.58). Этот случай был бы наилучшим для данного алгоритма, гарантируя логарифмическую зависимость времени выполнения для всех видов поиска. В действительно произвольной ситуации корнем может быть любой ключ, и поэтому полностью сбалансированные деревья встречаются исключительно редко, соответственно, без особых усилий не удастся сохранять дерево полностью сбалансированным после каждой вставки. Однако полностью несбалансированные деревья также встречаются редко при про-

Распечатано программой FinePnnt - Купитылулу finepnnt com