Лемма 12.2 Дерево бинарного поиска (BSI) - это бинарное дерево, с каждым из внутренних узлов которого связан ключ, причем ключ в любом узле больше (или равен) ключам и во всех узлах левого поддерева этого узла и меньше (или равен) ключам во всех узлах правого поддерева этого узла.

В программе 12.8 BST-деревья используются для реализации операций search, insert, construct и count. В первой части реализации узлы в BST-дереве определяются как содержащие элемент (с ключом), левую и правую связи. Кроме того, для обеспечения энергичной реализации операции count программа поддерживает поле, содержащее количество узлов в дереве. Левая связь указывает на BST-дерево с элементами с меньшими (или равными) ключами, а правая - на BST-дерево с элементами с большими (или равными) ключами.

Программа 12.8 Таблица символов на базе дерева бинарного поиска

В этой реализации функции search и insert используют приватные рекурсивные функции searchR и insertR, которые непосредственно отражают рекурсивное определение BST-дерева. Обратите внимание на использование аргумента ссылки в функции insertR (см. текст). Ссылка head указывает на корень дерева.

template <class Item, class Кеу> class ST {

private:

struct node

{ Item item; node *1, *r; node(Item x)

{ item = x; 1 = 0; r = 0; }

typedef node *link;

link head;

Item nullltem;

Item searchR (link h, Key v)

{ if (h == 0) return nullltem; Key t = h->itern.key 0 ; if (v == t) return h->item; if (v < t) return searchR(h->l, v); else return searchR(h->r, v) ;

void insertR (links h, Item x)

{ if (h = 0) { h = new node(x); return; } if (x.keyO < h->item.key 0)

insertR(h->l, x); else insertR(h->r, x);

public:

ST(int maxN)

{ head = 0; } Item search(Key v)

{ return searchR(head, v) ; } void insert(Item x)

{ insertR(head, x); }

При наличии этой структуры рекурсивный алгоритм поиска ключа в BST-дереве становится очевидным: если дерево пусто, имеет место промах при поиске; если ключ поиска равен ключу в корне, имеет место попадание при поиске. В противном случае выполняется поиск (рекурсивно) в соответствующем поддереве. Функция searchR в профамме 12.8 непосредственно реализует этот алгоритм. Мы вызываем рекурсивную подпрограмму, которая принимает дерево в качестве первого аргумента и ключ в качестве второго, начиная с корня дерева и искомого ключа. На каждом шаге гарантируется, что никакие части дерева, кроме текущего поддерева, не могут содержать элементы с искомым ключом.

Подобно тому как при бинарном поиске на каждой итерации размер интервала уменьшается чуть более чем в два раза, текущее поддерево в дереве бинарного поиска меньше предшествующего (в идеальном случае приблизительно вдвое). Процедура завершается либо в случае нахождения элемента с искомым ключом (попадание при поиске), либо когда текущее поддерево становится пустым (промах при поиске).

На диафамме в верхней части рис. 12.4 проиллюстрирован процесс поиска для примера дерева. Начиная с верхней части, процедура поиска в каждом узле приводит к рекурсивному вызову для одного из дочерних узлов этого узла; таким образом, поиск определяет путь по дереву. В случае попадания при поиске путь завершается в узле, содержащем ключ, а в случае промаха путь завершается во внешнем узле, как показано на средней диафамме на рис. 12.4.

В профамме 12.8 используется О связей для представления внешних узлов и приватные данные - член head, который является ссылкой на корень дерева. Для конструирования пустого BST-дерева значение head устанавливается равным 0. Можно было бы также использовать фиктивный узел в корне и еще один для представления всех внешних узлов в различных комбинациях, подобных рассмотренным для связных списков в табл. 3.1 (см. упражнение 12.53).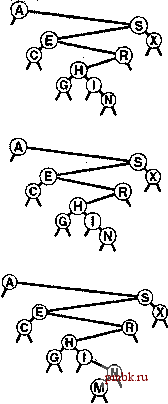

РИСУНОК 12.4 ПОИСК И ВСТАВКА В ДЕРЕВО БИНАРНОГО ПОИСКА

В процессе успешного поиска Не этом примере дерева (вверху) мы перемещаемся вправо от корня (поскольку И больше чем А), затем влево в правом поддереве (поскольку И меньше чем S) и т.д., продолжая перемещаться вниз по дереву, пока не встретится Н. В процессе неуспешного поиска М в этом примере дерева (в центре) мы перемещаемся вправо от корня (поскольку Мбольше чем А), затем влево в правом поддереве корня (поскольку Мменьше чем S) и т.д., продолжая перемещаться вниз по дереву, пока не встретится внешняя связь слева от Ne нижней части диаграммы. Для вставки М после обнаружения промаха при поиске достаточно просто заменить связь, которая прерывает поиск, связью с М (внизу).

Функция поиска в профамме 12.8 столь же проста, как и обычный бинарный поиск; существенная особенность BST-деревьев заключается в том, что операцию insert лтко реализовать в виде операции search. Рекурсивная функция uisertR для вставки нового элемента в BST-дерево следует логике, аналогичной использованной при разработке функции searchR, и использует ссылочный аргумент h для

построения дерева: если дерево пусто, h устанавливается равным ссылке на новый узел, содержащий элемент; если ключ поиска меньше ключа в корне, элемент вставляется в левое поддерево, в противном случае элемент вставляется в правое поддерево. То есть, аргумент ссылки изменяется только в последнем рекурсивном вызове, когда вставляется новый элемент. В разделе 12.8 и в главе 13 будут изучаться более сложные древовидные структуры, которые естественным образом представляются с помощью той же рекурсивной схемы, но которые чаще изменяют ссылочный аргумент.

На рис. 12.5 и 12.6 показан пример создания BST-дерева путем вставки последовательности ключей в первоначально пустое дерево. Новые узлы присоединяются к нулевым связям в нижней части дерева, а в остальном структура дерева никак не изменяется. Поскольку каждый узел имеет две связи, дерево растет скорее в ширину, нежели в высоту.

При использовании BST-деревьев реализация функции sort требует незначительного объема дополнительной работы. Построение BST-дерева сводится к сортировке элементов, поскольку при соответствующем рассмотрении BST-дерево представляет отсортированный файл. На приведенных выше рисунках ключи отображаются на странице слева направо (если не обращать внимания на их расположение по высоте и связи). Программа работает только со связями, но простой поперечный обход, по определению, обеспечивает выполнение этой задачи, что демонстрируется рекурсивной реализацией функции showR в программе 12.9. Для отображения элементов в BST-дереве в порядке их ключей мы отображаем элементы в левом поддереве в порядке их ключей (рекурсивно), затем корень, и далее элементы в правом поддереве в порядке их ключей (рекурсивно).

Программа 12.9 Сортировка с помощью BST-дерева

При поперечном обходе BST-дерева элементы посещаются в порядке следования их ключей. В этой реализации функция-член show элемента Item используется для вывода элементов в порядке следования их ключей.

private: void shcwR(link h, cstreamfi os)

if (h == 0) return; shcwR(h->l, cs); h->item.show(cs); shcwR(h->r, cs);

public: void show(cstreamfi cs) { shcwR(head, cs); }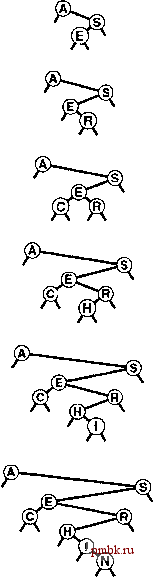

РИСУНОК 12.5 СОЗДАНИЕ ДЕРЕВА БИНАРНОГО ПОИСКА

Эта последовательность отражает результат вставки ключей AS Е R С НIN в первоначально пустое BST-дерево. Каждая вставка следует за промахом при поиске в нижней части дерева.