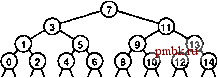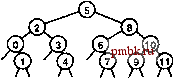Последовательность сравнений, выполняемых алгоритмом бинарного поиска, предопределена: конкретная последовательность используется в зависимости от значения искомого ключа и значения N. Сравнения могут быть описаны в виде структуры бинарного дерева, подобной приведенной на рис. 12.3. Это дерево аналогично использованному в главе 8 для описания размеров подфайлов во время сортировки слиянием (рис. 8.3). В бинарном поиске используется один путь в дереве, тогда как при сортировке слиянием - все пути. Это дерево является статическим и неявным; в разделе 12.5 будут рассматриваться алгоритмы, в которых для выполнения поиска используется динамическая, явно построенная структура бинарного дерева.

На верхней диаграмме показан поиск в файле, состоящем из 15 элементов, проиндексированных от О до 14. Мы просматриваем средний элемент (индекс 7), затем (рекурсивно) просматриваем левое поддерево, если искомый элемент меньше него, и правое - если он больше. Каждый поиск соответствует пути, проходящему по дереву сверху вниз; например, поиск элемента, который располагается между элементами 10 и 11, потребовал бы просмотра элементов 7, И, 9, 10. Для файлов с размерами, которые не являются на 1 меньше степени числа 2, последовательность не столь симметрична, что несложно заметить на нижней диаграмме, нарисованной для 12 элементов.

Одно из возможных усовершенствований бинарного поиска - более точное предположение о размещении ключа поиска в текущем интервале (вместо слепого сравнения его со средним элементом на каждом шаге). Эта тактика имитирует способ поиска имени в телефонном справочнике или слова в словаре: если искомая запись начинается с буквы, находящейся в начале алфавита, поиск выполняется вблизи начала книги, но если она начинается с буквы, находящейся в конце алфавита, поиск выполняется в конце книги. Для реализации данного метода, называемого интерполяционным поиском (interpolation search), программу 12.7 потребуется изменить следующим образом: оператор

m = (l+r)/2

заменяется на оператор

m = l+(v-[l] .key())*(r-l)/(a[r] .кеу()-а[1] .кеуО) ;

РИСУНОК 12.3 ПОСЛЕДОВАТЕЛЬНОСТЬ СРАВНЕНИЙ ПРИ БИНАРНОМ ПОИСКЕ

На этих диаграммах деревьев типа разделяй и властвуй показана последовательность индексов для сравнений при бинарном поиске. Последовательности зависят только от размера исходного файла, а не значений ключей в файле. Эти деревья несколько отличаются от деревьев, соответствующих сортировке слиянием и аналогичным алгоритмам (рис. 5.6 и 8.3), поскольку расположенный в корне элемент в поддеревья не включается.

Для обоснования изменения отметим, что выражение (/ + г)/ 2 равнозначно выражению l +-(r-l): мы вычисляем середину интервала, добавляя клевой граничной точке половину размера интервала. Использование интерполяционного поиска сводится к замене в этой формуле коэффициента - ожидаемой позицией ключа - а

именно (v- ki) / {кг- ki), где ki и кг означают значения а[1].кеу() и а[г].кеу(), соответственно. При этом предполагается, что значения ключей являются числовыми и равномерно распределенными.

Можно показать, что при интерполяционном поиске в файлах с произвольными ключами для каждого поиска (попадания или промаха) используется менее Ig IgiY сравнений. Доказательство этого утверждения выходит далеко за рамки этой книги. Эта функция растет очень медленно и на практике ее можно считать постоянной: если Л равно 1 миллиарду, то Ig IgA < 5. Таким образом, любой элемент можно найти, выполнив только несколько обращений (в среднем) - это существенное достижение по сравнению с бинарным поиском. Для ключей, которые распределены не вполне произвольно, производительность интерполяционного поиска еще выше. Действительно, фаничным случаем является метод поиска с использованием индексирования по ключам, описанный в разделе 12.2.

Однако интерполяционный поиск в значительной степени основывается на предположении, что ключи распределены во всем интервале более-менее равномерно - в противном случае, что обычно и имеет место на практике, метод окажется неэффективным. Кроме того, для его реализации требуются дополнительные вычисления. Для небольших значений стоимость обычного бинарного поиска (IgA) достаточно близка к стоимости интерполяционного поиска (Ig IgA), и поэтому вряд ли стоит использовать последний метод. С другой стороны, интерполяционный поиск определенно заслуживает внимания при работе с большими файлами, в приложениях, в которых сравнения выполняются особенно часто, и при использовании внешних методов, сопряженных с большими затратами на доступ.

Упражнения

> 12.34 Реализуйте нерекурсивную функцию бинарного поиска (см. программу 12.7).

12.35 Нарисуйте деревья, которые соответствуют рис. 12.3 для = 17 и = 24.

о 12.36 Найдите значения N, для которых бинарный поиск в таблице символов размером становится в 10, 100 и 1000 раз быстрее последовательного поиска. Предскажите значения аналитически и проверьте их экспериментально.

12.37 Предположите, что вставки в динамическую таблицу символов размера реализуются методом сортировки вставками, но для выполнения операции search используется бинарный поиск. Предположите, что поиск выполняется в 1000 раз чаще вставки. Определите в процентах долю времени, затрачиваемую на вставку, для yv= \0\ 10 10 и 10

12.38 Разработайте реализацию таблицы символов, в которой используется бинарный поиск и ленивая вставка, а также поддерживаются операции construct, count, search, insert и sort, прибегнув к следующей стратегии. Храните большой отсорти-

рованный массив для основной таблицы символов и неупорядоченный массив для недавно вставленных элементов. При вызове функции search отсортируйте недавно вставленные элементы (если таковые существуют), объедините их с основной таблицей, а затем воспользуйтесь бинарным поиском.

12.39 Добавьте ленивое удаление в реализацию, созданную в упражнении 12.38.

12.40 Ответьте на вопрос упражнения 12.37 для реализации из упражнения 12,38.

о 12.41 Реализуйте функцию, аналогичную бинарному поиску (программа 12.7), которая возвращает количество элементов в таблице символов с ключами, равными данному.

12.42 Создайте программу, которая при заданном значении Л создает последовательность макроинструкций, проиндексированных от О до 7V - 1, в форме compare(l, h), где /-ая инструкция в списке означает сравнить ключ поиска со значением индекса i в таблице; затем сообщить о попадании при поиске, если они равны, выполнить 1-ую инструкцию, если он меньще, и А-ую инструкцию, если он больще (индекс О зарезервируйте на случай промаха при поиске). Необходимо, чтобы последовательность обладала тем свойством, что для любого поиска должно выполняться столько же операций сравнения, как и при бинарном поиске в этом же наборе данных.

12.43 Расширьте макрос, созданный в упражнении 12.42, чтобы программа создавала машинный код, выполняющий бинарный поиск в таблице размером 7V при наименьшем возможном количестве машинных инструкций на одно сравнение.

12.44 Предположите, что a[i]==10*i для 1 < N. Сколько позиций в таблице исследуются интерполяционным поиском во время неуспешного поиска 2к- 1?

12.45 Найдите значения 7V, для которых интерполяционный поиск в таблице символов размером выполняется в 1, 2 и 10 раз быстрее бинарного поиска, при условии произвольности ключей. Предскажите значения аналитически и проверьте их экспериментально.

12.5 Деревья бинарного поиска

Для решения проблемы излишне высоких затрат на вставку в качестве основы для реализации таблицы символов используется явная древовидная структура.

Лежащая в основе структура данных позволяет разрабатывать алгоритмы с высокой средней производительностью выполнения операций search, insert, select и sort в таблицах символов. Этот метод используется во множестве приложений и в компьютерных науках считается одним из наиболее фундаментальных.

В главе 5 уже рассматривались деревья, тем не менее, полезно еще раз вспомнить терминологию. Определяющее свойство дерева (tree) заключается в том, что каждый узел указывается только одним другим узлом, называемым родительским (parent). Определяющее свойство бинарного дерева - наличие у каждого узла левой и правой связей. Связи могут указывать на другие двоичные деревья или на внешние (external) узлы, которые не имеют связей. Узлы с двумя связями называются также внутренними (internal) узлами. Для выполнения поиска каждый внутренний узел имеет также элемент со значением ключа, а связи с внешними узлами называются нулевыми (null) связями. Значения ключей во внутренних узлах сравниваются в ключом поиска и управляют протеканием поиска.