2a,N\nN0{N) 1пЛ + 0(1)

Таким образом, асимптотическая формула позволяет нам делать точные прогнозы, не вдаваясь в подробности реализации или анализа. Отметьте, что такое предсказание не было бы возможным, если бы 0-аппроксимация была задана только для главного члена.

Намеченный способ рассуждений позволяет ограничиться только главным членом при сравнении или предсказании времени выполнения алгоритмов. Зачастую мы подсчитываем время выполнения константно-временных операций и хотим Офаничить-ся только главным членом, подразумевая неявно, что точный анализ наподобие приведенного выше можно всегда провести, если потребуется.

Когда функция f{N) является асимптотически большой по сравнению с другой функцией g{N) (т.е. g{N) I f{N) -> О, когда -> ©о), мы иногда в книге используем терминологию (бесспорно нетехническую) порядка/(Л), подразумевая /(7V) + 0(g(7V)). То, что, кажется, теряется в математической точности, компенсируется доходчивостью, так как нас больше интересует производительность алгоритмов, а не математические детали. В таких случаях мы можем быть уверены в том, что при больших значениях N (если даже не при всех значениях) исследуемая величина будет близка по величине к /(7V). Например, даже если мы знаем, что величина равна Л(Л - 1)/2, мы можем говорить о ней, как N/ 2. Такой способ выражения результатов становится понятным быстрее, чем подробный и точный результат, и отличается от правильного значения всего лишь на 0.1 процента для, например, N = 1000. Потеря точности в данном случае намного меньше, чем при распространенном использовании 0{f{N)). Наша цель состоит в том, чтобы быть одновременно и точными, и краткими при описании производительности алгоритмов.

В похожем ключе мы иногда говорим, что время выполнения алгоритма пропорционально f{N), т.е. можно доказать, что оно равно cf{N) + g<7V), где g{N) асимптотически мало по сравнению с f{N). В рамках такого подхода мы можем предсказать время выполнения для 2N, если оно известно для N, как в примере, который обсуждался выше. На рис. 2.3 приводятся значения множителей для таких прогнозов поведения функций, которые часто возникают во время анализа аглорит-мов. В соединении с эмпирическим изучением (см. раздел 2.1) данный подход освобож-

РИСУНОК 2.3 ВЛИЯНИЕ УДВОЕНИЯ РАЗМЕРОВ ЗАДАЧИ НА ВРЕМЯ ВЫПОЛНЕНИЯ.

Прогнозирование влияния удвоения размеров задачи на время выполнения является простой задачей, когда время выполнения пропорционально одной из простых функций, как показано в таблице. В теории это влияние можно вычислить только когда N велико, но данный метод на удивление эффективен. И наоборот, быстрый метод определения функционального роста времени выполнения программы заключается в запуске программы, удвоении количество вводов для максимально возможного N, а затем оценка нового времени выполнения согласно приведенной таблице.

дает от определения постоянных величин, зависящих от реализации. Или же, применяя его в обратном направлении, мы можем часто разработать гипотезу о функциональной зависимости времени выполнения программы, изучив, как меняется время выполнения при увеличении Л в два раза.

Различия между 0-границами пропорционально (is proportional to) и порядка (about) проиллюстрированы на рис. 2.4 и 2.5. 0-нотация используется, прежде всего, для исследования фундаментального асимптотического поведения алгоритма; пропорционально требуется при экстраполяции производительности на основе эмпирического изучения, а порядка - при сравнении производительности разных алгоритмов или при предсказании абсолютной производительности.

Упражнения

1> 2.20 Докажите, что 0(1) - то же самое, что и 0(2).

2.21 Докажите, что в выражениях с 0-нотацией можно производить любое из перечисленных преобразований

/(УУ) 0(/(Л/)), cO(/(yV)) 0(/(7V)), 0{cf{N)) 0(f(N)),

/(TV) -giN)= dhm -f(N) =m + 0(h(N)), 0(f(N))0{giN)) 0(f{N)giN)), OinN))+ (MN)) OigiN)) если/(ТУ)= 0(g(TV)).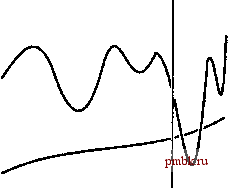

РИСУНОК 2.4 ОГРАНИЧЕНИЕ ФУНКЦИИ С ПОМОЩЬЮ О-АППРОКСИМАЦИИ

На этой схематической диаграмме осциллирующая кривая представляет собой функцию g(N), которую мы пытаемся аппроксимировать; гладкая черная кривая представляет собой другую функцию, f(N), которая используется для аппроксимации, а гладкая серая кривая является функцией cf(N) с некоторой неопределенной постоянной с. Вертикальная прямая задает значение Ng, указывающее, что аппроксимация справедлива для N > N. Когда мы говорим, что g(N) - 0(f(N)), мы ожидаем лишь то, что значение функции g(N) находится ниже некоторой кривой, имеющей форму функции f(N), и правее некоторой вертикальной прямой. Поведение функции f(N) может быть любым (например, она не обязательно должна быть непрерывной).

о 1.11 Покажите, что (TV+ \){Hn+ 0{\)) = N\nN+ 0(N).

2.23 Покажите, что Л1пЛ= OiN).

2.24 Покажите, что Л = 0(0.) для любого М и любого постоянного а > 1.

2.25 Докажите, что

г 1 л

yv+o(i)

= 1 + 0

1.16 Предположим, что = N. Найдите приближенную формулу, которая выражает к как функцию N.

1.11 Предположим, что lg(A:!) = N. Найдите приближенную формулу, которая выражает к как функцию N.

О 2.28 Известно, что время выполнения одного алгоритма равно O(NlogN), а другого - OiN). Что данное выражение неявно говорит об относительной производительности алгоритмов?

о 2.29 Известно, что время выполнения одного алгоритма всегда порядка 7V logTV, а другого - 0{N). Что данное выражение неявно говорит об относительной производительности алгоритмов?

о 2.30 Известно, что время выполнения одного алгоритма всегда порядка N\ogN, а другого - всегда порядка 7V\ Что данное выражение неявно говорит об относительной производительности алгоритмов?

о 2.31 Известно, что время выполнения одного алгоритма всегда пропорционально NlogN, а другого - всегда пропорционально N. Что данное выражение неявно говорит об относительной производительности алгоритмов?

о 2.32 Выведите значения множителей, приведенных на рис. 2.3: для каждой функции f(N), показанной слева, найдите асимптотическую формулу для /(2Л (N).

2.5 Простейшие рекурсии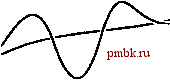

РИСУНОК 2.5 АППРОКСИМАЦИЯ ФУНКЦИЙ

Когда говорят, что функция g(N) пропорциональна функции f(N) (верхний график), то подразумевают, что она растет как f(N), но, возможно, смещена относительно последней на неизвестную постоянную. Если задано некоторое значение g(N), можно предсказать поведение функции при больших N. Когда говорят, 4mog(N) порядка f(N) (нижний график), то подразумевают, что функцию f можно использовать для более точной оценки значений функции g.

Как мы увидим далее в этой книге, многие алгоритмы основаны на принципе рекурсивного разбиения большой задачи на меньшие, когда решения подзадач используются для решения исходной задачи. Эта тема подробно обсуждается в главе 5, в основном, с практической точки зрения, где основное внимание уделено различным реализациям и приложениям. Кроме того, в разделе 2.6 приводится подробный пример. В этом разделе исследуются простейшие методы анализа таких алгоритмов и вывод решений нескольких стандартных формул, которые возникают при анализе многих изучаемых алгоритмов. Понимание математических свойств формул в этом разделе дает необходимое понимание свойств производительности алгоритмов.

Рекурсивное разбиение алгоритма напрямую проявляется в его анализе. Например, время выполнения подобных алгоритмов определяется величиной и номером подзадачи, а также временем, необходимым для разбиения задачи. Математически зависимость времени выполнения алгоритма для ввода величиной N от времени выполнения при меньшем количестве вводов легко задается с помощью рекуррентных соотношений. Такие формулы точно описывают производительность алгоритмов: для вычисления времени выполнения необходимо решить эти рекурсии. Более строгие