значения Р приводит к уменьшению числа проходов, но в то же время увеличивает количество операций (медленных) непоследовательного доступа.

Упражнения

> 11.35. Показать, как ключи EASYQUESTIONWITHPLENTYOF KEYS сортируются посредством 3-путевого сбалансированного слияния в стиле примера, представленного на рис. 11.12.

> 11.36. Как отразится на числе проходов многопутевого слияния тот факт, что число используемых для слияния внешних устройств удвоилось?

011.37. Как отразится на числе проходов многопутевого слияния тот факт, что мы увеличили в 10 раз объем доступного пространства оперативной памяти?

11.38. Разработать интерфейс для внешнего ввода и вывода, который предусматривает последовательную передачу блоков данных с внешних устройств, работающих асинхронно (или детально изучить существующий в вашей системе). Использовать этот интерфейс для реализации /-путевого слияния, при этом Р есть максимально возможное в конкретных обстоятельствах, но Р входных файлов и выходной файл должны размещаться на различных выходных устройствах. Сравните время выполнения полученной программы с временем, необходимым для копирования файлов на выходные устройства, один за другим.

11.39. Используйте интерфейс из упражнения 11.38 при написании программы замены порядка на обратный для файла максимально допустимого в вашей системе размера.

11.40. Как вы будете выполнять идеальное тасование всех записей на внешнем устройстве?

11.41. Разработать стоимостную модель многопутевого слияния, которая охватывает атгоритмы, способные переключаться с одного файла на другой на одном и том же устройстве с постоянной стоимостью переключения, которая намного превышает стоимость последовательного чтения.

11.42. Разработать подход к внешней сортировке, который основан на разделении, подобном используемому в быстрой сортировке или в поразрядной сортировке MSD (сначала по старшей цифре), проанализировать его и сравнить с многопутевой сортировкой. Вы можете перейти на более высокий уровень абстракции, использованный при описании сортировки-слияния в этом разделе, однако вы должны стремиться к тому, чтобы быть способными спрогнозировать время выполнения для заданного числа устройств и заданного объема оперативной памяти.

11.43 Как вы будете сортировать содержимое внешнего устройства, если любые другие внешние устройства недоступны для использования (можно пользоваться только оперативной памятью)?

11.44. Как вы будете сортировать содержимое внешнего устройства, если для использования доступно всего лишь еще одно устройство (а также оперативная память)?

11.4. Различные реализации сортировки-слияния

Общая стратегия сортировки-слияния, описанная в разделе П. 13, доказала свою эффективность на практике. В этом разделе мы рассмотрим два усовершенствования этой стратегии, позволяющих снизить объем затрат. Первое из них, метод выбора с замещением (replacement selection), оказывает на время выполнения тот же эффект, что и объем пространства используемой оперативной памяти; следующий метод, многофазное слияние (polyphase merging), обеспечивает тот же эффект, что и увеличение числа используемых нами устройств.

В разделе 11.3 мы обсуждали применение очереди по приоритетам для У-путевого слияния, но при этом делали оговорку, что Р настолько мало, что усовершенствование алгоритма с целью повышения быстродействия фактически незаметны. Тем не менее, во время начального распределения мы можем воспользоваться быстрыми очередями по приоритетам, чтобы получить отсортированные отрезки файлов, размеры которых не позволяют размещать их в оперативной памяти. Идея заключается в том, чтобы пропустить (неупорядоченные) входные данные через очередь по приоритетам больших размеров, как и раньше, записывая в очередь по приоритетам наименьший элемент, постоянно заменяя его следующим элементом со входа с одним дополнительным условием: если новый элемент меньше, чем только что появившийся на выходе, то поскольку он может и не стать частью текущего сортируемого блока, мы маркируем его как принадлежащий следующему блоку и считаем, что он больше всех остальных элементов текущего блока. Когда маркированный элемент поднимается в вершину очереди по приоритетам, мы начинаем новый блок. На рис. 11.14 этот метод показан в действии.

Лемма 11.5. В случае произвольных ключей размеры блоков данных, полученных посредством выборки с замещением, в два раза превосходят размер сортирующего дерева.

Если мы воспользуемся пирамидальной сортировкой для получения исходных блоков данных, мы заполним записями всю оперативную память; в этом случае нужно выводить их из памяти одну за одной до тех пор, пока сортирующее дерево не опустеет. После этого мы заполняем оперативную память очередным пакетом записей и продолжаем этот процесс снова и снова. В среднем сортирующее дерево занимает во время выполнения этого про-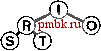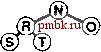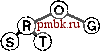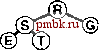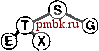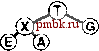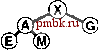

РИСУНОК 11.14. ВЫБОР С ЗАМЕЩЕНИЕМ

Эта последовательность показывает, как можно получить два блока данных, AIN О RSTX uAEEGLMP, соответственно, длиной 7 и 8, из

последовательности, используя для этой цели сортирующее дерево размером 5.

цесса только половину пространства оперативной памяти. В противоположность этому, выборка с замещением сохраняет эту же структуру в оперативной памяти, так что не следует удивляться тому, что ее эффективность в два раза выше. Полное доказательство этой леммы требует полного и разностороннего анализа {см. раздел ссылок), хотя это утверждение нетрудно проверить экспериментальным путем (см. упражнение 11.47).

Что касается файлов с произвольной организацией, то практический результат применения выборки с замещением, по-видимому, состоит в уменьшения числа проходов на 1: вместо того, чтобы начинать с отсортированных блоков данных, размер которых примерно равен объему пространства оперативной памяти, мы для начала можем использовать отрезки в два раза большего объема пространства оперативной памяти. Для Р - 2 такая стратегия экономит точно один проход слияния, для значений Р больше 2 полученный эффект несколько скромнее. Тем не менее, мы знаем, что на практике сортировка файлов с произвольной организацией случается довольно редко, и если ключи упорядочены в той или иной степени, то в условиях использования метода выборки с замещением можно получать отрезки огромных размеров. Например, если ни Одному из ключей не предшествуют в файле более М ключей, превосходящих его по значению, то этот файл может быть полностью отсортирован за один проход выборки с замещением, и при этом никакое слияние не понадобится! Эта возможность служит наиболее веским аргументом в пользу практического применения выборки с замещением.

Большим недостатком сбалансированной многопутевой сортировки является тот факт, что примерно только половина внешних устройств активно используется во время выполнения процедур слияния: Р входных устройств и устройство, используемое для накопления выхода. Альтернативой этому остается выполнение {2Р-- 1)-пу-тевых сортировок с передачей выхода на устройство О, с последующим распределением данных на другие магнитные ленты в конце каждого прохода слияния. Но этот подход не превосходит первый по эффективности, поскольку он удваивает количество проходов, что обусловлено необходимостью распределения данных. Сбалансированное многопутевое слияние, по-видимому, потребует либо дополнительного числа лентопротяжных устройств, либо выполнения дополнительных операций копирования. Разработаны несколько хитроумных алгоритмов, которые обеспечивают занятость всех внешних устройств за счет замены устройства, на котором производится слияние отсортированных блоков данных небольших размеров. Простейший из этих методов получил название многофазное слияние {polyphase merging).

Основополагающая идея многофазного слияния заключается в том, чтобы распределять отсортированные блоки, полученные в результате выполнения выборки с замещением на доступные лентопротяжные устройства с определенной степенью неравномерности (оставляя одно устройство пустым) с последующим применением стратегии сливать до опустошения {merge-until-empty): поскольку сливаемые ленты неодинаковы по длине, одна из них будет исчерпана раньше остальных, после чего она может быть использована как выходная. То есть, мы меняем ролями выходную ленту (теперь на ней размещены несколько отсортированных блоков) и пустую к этому моменту входную ленту, продолжая этот процесс до тех пор, пока останется только один блок. На рис. 11.15 показан соответствующий пример.