Связь между идеальным тасованием и сетями Бэтчера позволяет завершить наши исследования сетей сортировки анализом одной забавной версии рассматриваемого алгоритма. Если мы перетасуем линии нечетно-четного слияния Бэтчера, то получим сети, в которых компараторы соединяют смежные линии. Рисунок 11.8 служит иллюстрацией сети, которая соответствует реализации тасования, соответствующего программе 11.2. Эту схему межкомпонентных соединений иногда называют сачком для ловли бабочек (butterfly network). На этом рисунке дано еще одно представление той же неветвящейся программы, которая предлагает еще более унифицированный шаблон: она использует только операции полного тасования.

На рис. 11.9. показана еще одна интерпретация рассматриваемого метода, которая служит иллюстрацией базовой структуры. Во-первых, мы записываем один файл под другим, далее, мы сравниваем смежные по вертикали элементы и при необходимости выполняем их обмен так, чтобы меньший элемент находился выше большего. Затем мы делим каждый ряд на две равных части и чередуем половины этих рядов, после чего выполняем те же операции сравнения-обмена над числами во второй и третьей строках. В сравнении других пар рядов нет необходимости, поскольку они были предварительно отсортированы. Операция деления и чередования оставляет как ряды, так и столбцы в отсортированном виде. Это свойство в общем виде сохраняется благодаря той же операции: каждый шаг удваивает число рядов, сокращает наполовину число столбцов и сохраняет ряды и столбцы в отсортированном виде, в конечном итоге мы получаем один столбец и рядов, благодаря чему столбец полностью отсортирован. Связь между таблицей, представленной на рис. 11.9 и сетью, изображенной в нижней части рис. 11.8, заключается в том, что когда мы разворачиваем таблицы по столбцам (за элементами первого столбца следуют элементы второго столбца и т.д.) мы замечаем, что перестановка, необходимая для перехода с одного шага на другой, есть ни что иное как идеальное тасование.

Теперь с помощью абстрактной параллельной машины со встроенными межкомпонентными соединениями для идеальной сортировки, как показано на рис. 11.10, мы имеем возможность непосредственно

а egg i mnrabe е lmpx

РИСУНОК 11.9. СЛИЯНИЕ МЕТОДОМ ДЕЛЕНИЯ И ЧЕРЕДОВАНИЯ.

Записав вначале оба отсортированных файла в один ряд, мы выполняем их слияние посредством многократного повторения следующий процедуры: разбиваем каждый ряд на две равные части и чередуем полученные половины (слева), после чего выполняем операции сравнения-обмена над смежными по вертикали элементами, содержащимися в различных рядах (справа). Сначала у нас было 16 столбцов и 1 ряд, затем восемь столбцов и 2 ряда, далее 4 столбца и четыре ряда, потом 2 столбца и восемь рядов и, наконец, 16 рядов и один столбец, который предстает в отсортированном виде.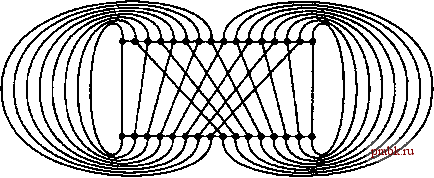

РИСУНОК 10.10. МАШИНА ИДЕАЛЬНОГО ТАСОВАНИЯ

Изображенная на этом рисунке машина с межкомпонентными связями способна эффективно выполнять алгоритм Бэтчера (равно как и множество других). Подобные связи используются в некоторых параллельных компьютерах.

реализовать сеть, подобную показанной в нижней части рис. 11.8. Такая машина на каждом шаге выполняет предусмотренные рассматриваемым алгоритмом операции сравнения-обмена на некоторой паре смежных процессоров, после чего осуществляет идеальное тасование данных. Программирование работы этой машины сводится к определению, какие пары процессоров должны выполнять операции сравнения-обмена на каждом цикле.

На рис. 11.11. показаны динамические характеристики как восходящего метода, так и версии нечетно-четного слияния Бэтчера с полным тасованием.

Тасование - это важная абстракция, описывающая движение данных в алгоритмах, построенных по принципу разделяй и властвуй , и она возникает в различных задачах, отличных от сортировки. Например, квадратная матрица размером 2-на-2 хранится в развернутом по рядам виде, затем п идеальных тасовок транспонируют эту матрицу (приводят матрицу к развернутому по столбцам виду). В число более важных примеров входят быстрые преобразования Фурье и полиномиальное приближение (см часть 8). Мы можем решить каждую из этих задач, воспользовавшись циклической машиной идеального тасования, подобной показанной на рис. 11.10, но с гораздо более мощными процессорами. Мы можем даже обдумать вариант с использованием универсальных процессоров, способных выполнять прямое и обратное тасование (некоторые из машин этого типа были даже построены для практического применения); мы вернемся к обсуждению параллельных машин данного типа в разделе 11.5.

Упражнения

11.16. Дать примеры сетей сортировки четырех (см. упражнение 11.6), пяти и шести элементов. Использовать минимально возможное число компараторов.

о 11.17. Написать программу, способную подсчитать число параллельных шагов, необходимых для выполнения любой неветвящейся программы. Совет: Воспользуйтесь следующей стратегией присвоения меток. Отметьте входные линии как принадлежащие к каскаду О, затем для каждого компаратора выполните следующие действия: пометьте обе выходные линии как входные для каскада / + 1, если метка одной из входных линий есть /, а метка другой линии не превосходит /.

11.18. Сравнить время выполнения программы 11.4 с аналогичным показателем для программы 8.3 для случайно упорядоченных ключей при N= 10, 10 10 и 10

[>11.19. Начертить сеть Бэтчера, ориентированную на слияние типа Ю-с-П.

11.20. Доказать существование зависимости между рекурсивным обратным тасованием и тасованием, представленном на рис. 11.8.

о 11.21. Из изложенного в тексте следует, что на рис. 11.7 в неявном виде представлено 11 сетей сортировки 21 элемента. Начертить ту из них, которая содержит минимальное число компараторов.

11.22. Найти число компараторов в нечетно-четной сетях сортировки Бэтчера для 2 < n < 32, где сети, когда Л не есть степень 2, строятся на базе первых n линий сети, построенной для наименьщей степени 2, превосходящей n.

о 11.23. Для = 2 вывести точное выражение для определения числа компараторов, используемых в нечетно-четной сетях сортировки Бэтчера. Совет: Проверьте свой ответ на данных рис. 11.7, которые показывают, что в сетях имеются 1, 3, 9, 25 и 65 компараторов для равного, соответственно, 2, 4, 8, 16 и 23.

о 11.24. Построить сеть для сортировки 21 элемента, выбрав для этой цели нисходящий рекурсивный стиль, когда сеть размером n представляет собой композицию сетей размером In/ 2j и ГЛ/21, за которыми следует сеть слияния. (Воспользоваться рещением упражнения 11.19 в качестве заверщающей части сети.)

11.25. Воспользоваться рекуррентными соотнощениями для подсчета числа компараторов в сетях сортировки, построенных, как описано в упражнении 11.24 для 2 < n < 32. Сравните полученные вами результаты с результатами, полученными в упражнении 11.22.

11.26. Найти 16-линейную сеть сортировки, которая использует меньшее число компараторов, чем сеть Бэтчера.

11.27. Вычертить сети слияния, соответствующие рис.11.8, для битонных последовательностей, используя схему, описанную в упражнении 11.14.

11.28. Вычертить сети сортировки, соответствующие сортировке Шелла с приращениями Пратта (см. раздел 6.6) для n = 32.

11.29. Построить таблицу, содержащую число компараторов в сетях, описанных в упражнении 11.28, и число компараторов в сетях Бэтчера для jV= 16, 32, 64, 128 и 256.

11.30. Разработать сети сортировки, способные выполнять сортировку 3-сортированных или 4-сортированных файлов из N элементов.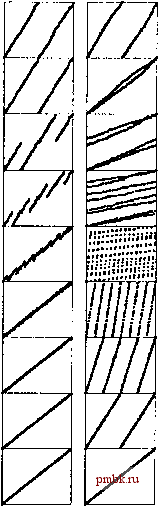

РИСУНОК 11.11. ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ НЕЧЕТНО-ЧЕТНОГО СЛИЯНИЯ. Восходящая версия нечетно-четного слияния (слева) использует последовательность каскадов, посредством которых выполняется операция сравнения-обмена большей половины одного отсортированного файла с меньшей половиной следующего. При добавлении полного тасования (справа) рассматриваемый алгоритм приобретает совершенно другой вид.