Рисунок 11.7 служит иллюстрацией сети нечетно-четной сортировки Бэтчера, построенной на основе Сетей слияния, представленных на рис. 11.5, с использованием стандартной конструкции рекурсивной сортировки слиянием. Эта конструкция дважды рекурсивна: один раз для сетей слияния, другой раз - для сетей сортировки. И хотя они не оптимальны - мы вскоре рассмотрим оптимальные сети - тем не менее, они достаточно эффективны.

Программа 11.3. Нечетно-четное слияние Бэтчера (нерекурсивная версия)

Данная реализация нечетно-четного слияния (которая предполагает, что размер файла N является степенью 2) компактна и своеобразна. Мы сможем понять как она совершает процедуру слияния, выполнив исследования, в какой степени она соответствует рекурсивной версии (см. программу 11.2 и рис. 11.5). Она завершает слияние за 1дЛ/ проходов, представленных единообразными и независимыми командами сравнения-обмена.

template <class Item>

void merge (Item a[], int 1, int m, int r) { int N = r-1+1; предполагается, что

N/2 это m-1+1 for (int к = N/2; Ic > 0; Jc /= 2) for (int j = Jc % (N/2); j+]c<N; j+= Ic+lc) for (int i = 0; i < k; i++)

сопфвхсЬ(а[1+j+i], a[l+j+i+k]);

Лемма 11.3. Сети нечетно-четной сортировки Бэтчера используют приблизительно N(\gNf / 4 компараторов и могут быть выполнены за (IgN) / 2 параллельных шагов.

Сеть слияния требует выполнения около \$N параллельных шагов, а сети сортировки требуют выполнения 1 + 2 \$N или примерно (IgAV 2 параллельных шагов. Подсчет компараторов оставляем читателю в качестве упражнения (см. упражнение 11.23).

Использование функции слияния в программе 11.3 в рамках стандартной сортировки слиянием, представленной программой 8.3, позволяет получить компактный обменный неадаптивный метод сортировки, который использует 0{N(\gN)) операций сравнения-обмена. С другой стороны, мы можем удалить все рекурсии из сортировки слиянием и непосредственно реализовать восходящую версию в полном ее объеме, как показано в программе 11.4. Как и в случае программы 11.3, эту профамму легче понять, если рассматривать ее как чередующееся представление сети, показанной на рис. 11.7.

ag i norstaeelmpxy А А

l :, . n

и о

aeelmpstag i norxy

, . А -м

а е е l а g а е g l

nmpstorxy

n р

о s r т

aeagel i nmporstxy

: а е :

е g

i l м n

aaeegi lmnoprstxy

РИСУНОК 11.6. ПРИМЕР НЕЧЕТНО-ЧЕТНОГО СЛИЯНИЯ БЭТЧЕРА.

Если удалить все операции тасования, то для выполнения слияния Бэтчера применительно к нашему примеру потребуется 25 операций слияния-обмена, изображенных на этой диаграмме. Их можно разбить на четыре фазы выполнения независимых операций сравнения-обмена с фиксированным сдвигом каждой фазы.

РИСУНОК 11.7. НЕЧЕТНО-ЧЕТНЫЕ СЕТИ СОРТИРОВОК БЭТЧЕРА

Данная сеть сортировки на 32 линии содержит две копии сетей на 16 линий, четыре копии сетей на восемь линий и т.д. Просматривая справа налево, мы как бы проходим через всю структуру сверху вниз: сеть сортировки на 32 линии состоит из сети слияния типа 16-С-16, за которой следуют две копии сети сортировки на 16 линий (одна в верхней половине и одна в нижней половине). Каждая сеть на 16 линий состоит из сети слияния типа 8-с-8, за которой следуют две копии сети сортировки на 8линий и т.д. Просматривая слева направо, мы проходим через эту структуру снизу вверх: первый столбец компараторов создает отсортированный файл размером 2; далее идут сети слияния типа 2-с-2, которые создают отсортированные подфайлы размером 4; затем идут сети слияния типа 4-с-4, которые создают сортированные подфайлы размером 8 и т.д.

Такая реализация предусматривает включение еще одного цикла и одной проверки в программу 11.3, поскольку слияние и сортировка обладают похожими рекурсивными структурами. Чтобы выполнить восходящий проход слияния последовательности отсортированных файлов размера 2* в последовательность отсортированных файлов размера 2*, мы используем всю сеть слияния, но при этом включаем только те компараторы, которые полностью попадают в подфайлы. Данная программа может претендовать на получение приза как наиболее компактная нетривиальная реализация сортировки, какую нам когда-либо приходилось видеть и которая может оказаться наилучшим выбором в тех случаях, когда мы хотим воспользоваться всеми преимуществами высокопроизводительных архитектурных особенностей для высокоскоростной сортировки небольших файлов (или для построения сетей сортировки). Понимание того, как и почему сортирует рассматриваемая программа, может оказаться неподъемной задачей, если мы лишимся перспективы использования рекурсивных приложений и сетевых конструкций, рассмотренных до сих пор.

Как это часто случается с методами типа разделяй и властвуй , мы сталкиваемся с двумя возможностями для выбора в случае, когда Л не есть степенью 2 (см. упражнение 11.24 и 11.21). Мы можем поделить его напополам (сверху вниз) либо разделить на максимальное число, представляющее собой степень 2, меньшее N (снизу вверх). Последнее несколько удобнее для сетей сортировки, поскольку это эквивалентно построению полной сети для минимальной степени 2, большей или равной 7V, после чего использовать только первые 7V линий и компараторы, оба конца которых подключены именно к этим линиям. Предположим теперь, что на неиспользованных линиях имеются служебные ключи, которые больше любых других ключей сети. Тогда компараторы на этих линиях никогда не производят операций обмена, так что их

можно удалить без ущерба для дальнейших действий. В самом деле, мы можем воспользоваться любым смежным набором из линий большей сети: будем считать, что на игнорируемых линиях в верхней части имеются сигнальные метки с небольшими значениями, а на игнорируемых линиях в нижней части имеются служебные метки с большими значениями. Во всех этих сетях имеется примерно N {\gNf / А компараторов.

Программа 11.4. Нечетно-четная сортировка Бэтчера (нерекурсивная версия)

Данная реализация нечетно-четной сортировки Бэтчера прямо соответствует представлению сети, отображенному на рис. 11.7. Она разбивается на фазы, индексируемые переменной р. Последняя фаза, когда р равно W, и есть нечетно-четное слияние Бэтчера. Предпоследняя фаза, когда р равно N/2, есть нечетно-четное слияние с первым каскадом, и все компараторы, которые пересекаются с любой линией, кратной N/2, удаляются; третья фаза с конца, когда р равно W/4, есть нечетно-четное слияние с двумя первыми каскадами, а все компараторы, которые пересекаются с любой линией, кратной W/4, удаляются, и так далее.

template <class Item>

void batchersort(Item a[], int 1, int r) { int N = r-1+1; for (int p = 1; p < N; p += p) for (int к = p; к > 0; к /= 2) for (int j = k%p; j+k < N; j += (k+k)) for (int i = 0; i < N-j-k; i++) if ((j+i)/(p+p) = (j+i+k)/(p+p)) compexch(a[1+j+i], a[1+j+i+k]);

Теория сетей сортировки развивалась достаточно интересно {см. раздел ссылок). Задача построения сети с минимально возможным числом компараторов была поставлена Бозе (Bose) еще до 1960 г., впоследствии она получила название задачи Бозе-Нельсона (Bose-Nelson). Сети Бэтчера были первым более-менее приемлемым решением этой задачи, а некоторые исследователи даже полагали, что сети Бэтчера оптимальны. Сети слияния Бэтчера оптимальны, так что любая сеть сортировки с существенно меньшим числом компараторов может быть построена только в рамках подхода, отличного от рекурсивной сортировки слиянием. Задача нахождения оптимальных сетей сортировки не подвергалась исследованиям до тех пор, пока в 1983 г. Аджтай (Ajtai), Колмос (Kolmos) и Шемереди (Szemeredy) не доказали существования сетей с 0(N\ogN) числом компараторов. Однако сети AKS (Ajtai, Kolmos и Szemeredy) - это всего лишь математические умозаключения, не имеющие практического применения, так что сети Бэтчера все еще считаются одними из наиболее подходящих для практического применения.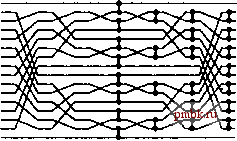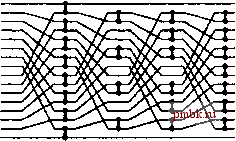

РИСУНОК 11.8.

Прямая реализация программы 11.2 как сети сортировки порождает сеть, насыщенную рекурсивными операциями тасования и обратного тасования (вверху). Эквивалентная реализация (внизу) использует только операции полного тасования.