причин выполняется на новой машине лучше других, но также и то, можно ли в рамках того или иного нового алгоритма воспользоваться конструктивными особенностями конкретной машины. Чтобы разработать новый алгоритм, мы даем определение некоторой абстрактной машины, которая инкапсулирует основные свойства реальной машины, разрабатываем и анализируем алгоритмы для этой абстрактной машины, затем пишем программы лучших алгоритмов, тестируем эти программные реализации, после чего вносим усовершенствования как в сами алгоритмы, так и в их программные реализации. С этой целью мы воспользуемся сведениями, полученными нами при изучении материалов, изложенных в главах 6-10, в том числе и описаниями многих методов, ориентированных на выполнение на машинах общего назначения. В то же время абстрактные машины налагают на эти алгоритмы ряд ограничений, которые помогут нам учесть реальные затраты и убедиться в том, что каждый алгоритм достигает максимальной эффективности на том или ином конкретном виде машины.

На одном конце спектра находятся модели низкого уровня, в рамках которых разрешается выполнение только операции сравнения-обмена. На другом конце спектра находятся модели высокого уровня, в условиях которых мы выполняем считывание и запись блоков данных больших объемов на медленнодействующие внешние носители информации или распределяем данные между параллельными процессорами.

В первую очередь мы рассмотрим версию сортировки слиянием, известную как нечетно-четная сортировка слиянием Бэтчера {Batchers odd-even mergesort). В ее основу положен алгоритм слияния, функционирующий по принципу разделяй и властвуй, который использует только операции сравнения-обмена, при этом для перемещения данных употребляются операции идеального тасования {perfect-shuffle) и операция идеального обратного тасования {perfect unshuffle). Они представляют интерес сами по себе и применяются для решения проблем, отличных от сортировки. Далее мы будем рассматривать метод Бэтчера как сеть сортировки. Сеть сортировки {sorting network) представляет собой простую абстракцию для аппаратных средств сортировки. Такая сеть состоит из соединенных друг с другом посредством межкомпонентных связей компараторов {comparators), представляющих собой модули, способные выполнять операции сравнения-обмена.

Другой важной проблемой абстрактной сортировки является проблема внешней сортировки {external sorting); в этом случае сортируемый файл обладает такими огромными размерами, что не помещается в оперативной памяти. Стоимость доступа к индивидуальным записям может оказаться непомерно высокой, в силу этого обстоятельства мы должны использовать абстрактную модель, в которой записи передаются между внешними устройствами в виде блоков больших размеров. Мы рассмотрим два алгоритма внешней сортировки и воспользуемся соответствующей моделью, чтобы сравнить их между собой.

В заключение мы рассмотрим параллельную сортировку {parallel sorting) на тот случай, когда сортируемый файл распределяется между независимыми параллельными процессорами. Мы дадим определение простой модели параллельной машины, а затем выясним, при каких условиях метод Бэтчера обеспечит эффективное решение этой проблемы. Использование одного и того же базового алгоритма для проблем

высокого уровня и низкого уровня служит наглядной иллюстрацией того, какой мощью обладает абстракция.

Различные абстрактные машины, рассматриваемые в этой главе, достаточно просты, однако заслуживают подробного изучения, поскольку инкапсулируют в себе конкретные ограничения, которые могут оказаться критичными для некоторых приложений сортировки. Аппаратные средства сортировки низкого уровня должны состоять из простых компонентов; внешняя сортировка в общем случае требует поблочного доступа к особо крупным файлам данных, а параллельная сортировка накладывает определенные ограничения на связи с процессорами. С одной стороны, мы не можем в полной мере воспользоваться подробной моделью машины, которая полностью соответствует конкретной реальной машине, с другой стороны, абстракции, которые мы рассматриваем, приводят нас не только к теоретическим формулировкам, содержащим информацию о наиболее важных ограничениях, но также и к весьма интересным алгоритмам, которые можно использовать непосредственно на практике.

11.1 Четно-нечетная сортировка слиянием Бэтчера

Для начала мы рассмотрим метод сортировки, в основе которых лежат две следующих абстрактных операции: операция сравнения обмена {compare-exchange) и операция идеального тасования {perfect shuffle) (вместе с ее антиподом, операцией идеального обратного тасования {peifect unshuffle)). Алгоритм, разработанный Бэтчером в 1968 г., известен как нечетно-четная сортировка слиянием Бэтчера {Batchers odd-even mergesort). Реализовать алгоритм, используя операции тасования, сравнения-обмена и двойной рекурсии, несложно; гораздо труднее понять, почему алгоритм работает, и распутать все тасования и рекурсии, чтобы понять, как он работает на нижнем уровне.

Мы уже подвергали беглому анализу операцию сравнения-обмена в главе 6, где отметили, что некоторые рассматриваемые при этом элементарные методы сортировки могут быть четко выражены в терминах этой операции. В настоящий момент нас интересуют методы, в условиях которых данные проверяются исключительно через операций сравнения-обмена. Стандартные операции сравнения исключаются: операции сравнения-обмена не возвращают результат, следовательно, у программы нет возможности выполнять те или иные действия в зависимости от конкретных значений данных.

Определение 11.1 Неадаптивный алгоритм сортировки - это алгоритм, в котором последовательность выполняемых операций зависит только от числа входных данных, а не от значений ключей.

В этом разделе мы допускаем использование операций, которые в одностороннем порядке выполняют переупорядочивание данных, такие как операции обмена и тасования, но без этих операций, как мы увидим в разделе 11.2, можно обойтись. Неадаптивные методы эквивалентны неветвящимся программам сортировки: они могут быть записаны в виде простого перечня операций сравнения-обмена.

Например, последовательность

compexch(а[О], а[1]) compexch(а[1], а[2]) compexch(а[О], а[1])

суть неветвящаяся программа, выполняющая сортировку трех элементов. Мы используем циклы, тасования и другие операции высокого уровня, преследуя цель удобной и экономной записи алгоритма, однако основная цель при разработке алгоритма состоит в том, чтобы определить для каждого N фиксированную последовательность операций compexch, которые способны выполнить сортировку любого набора из N ключей. Мы можем без ущерба для общности рассуждений предположить, что ключи принимают целочисленные значения в диапазоне от 1 до N {см. упражнение 11.4); чтобы убедиться в том, что неветвящаяся программа работает правильно, достаточно доказать, что она сортирует каждую из возможных перестановок этих значений (см., например, упражнение 11.5).

Лищь немногие из алгоритмов, которые мы успели обсудить в главах 6-10, являются неадаптивными алгоритмами - все они используют операцию operator< либо проверяют ключи каким-то другим способом, после чего выполняют действия в зависимости от значений ключей. Исключением является пузырьковая сортировка (см. раздел 6.4), в условиях которой используются только операции сравнения-обмена. Версия Пратта сортировки методом Шелла (см. раздел 6.6) служит еще одним примером неадаптивного метода сортировки.

Программа 11.1 представляет собой реализацию других абстрактных операций, которыми мы будем пользоваться в дальнейшем - операции идеального тасования и операции обратного идеального тасования (на рис. 11.1 дается пример каждой из них). Идеальное тасование переупорядочивает массив так, как может перетасовать колоду карт только большой специалист этого дела: колода делится точно наполовину, затем карты по одной берутся из каждой половины колоды. Первая карта всегда берется из верхней половины колоды. Если число карт в колоде четное, в обеих половинах содержится одинаковое их число, если число карт нечетное, то лишняя карта идет последней в верхней половине колоды.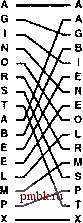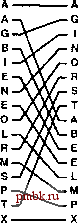

РИСУНОК 11.1. ИДЕАЛЬНОЕ ТАСОВАНИЕ И ОБРАТНОЕ ИДЕАЛЬНОЕ ТАСОВАНИЕ

При выполнении идеального тасования (слева) мы берем первый элемент файла, затем первый элемент из второй половины файла, затем второй элемент файла и второй элемент из второй половины файла и т. д. Предположим, что элементы перенумерованы сверху вниз, начиная с 0. Следовательно, элементы из первой половины занимают позиции с четными номерами, а элементы из второй половины занимают нечетные позиции. Чтобы выполнить обратное идеальное тасование (справа), мы должны выполнить обратную процедуру: элементы, занимаюиие четные позиции, переходят в первую половину файла, элементы, занимаюшие нечетные позиции, - во вторую половину.

Распечатано программой FmePnni - Купи