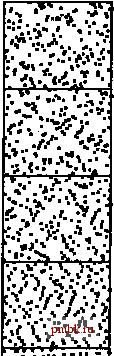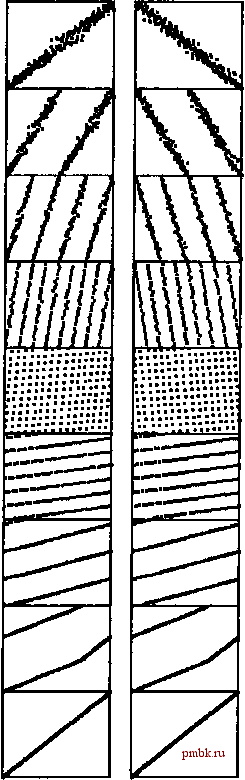
РИСУНОК 10.17. ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОРАЗРЯДНОЙ СОРТИРОВКИ LSD ДЛЯ РАЗЛИЧНЫХ ВИДАХ ФАЙЛОВ

Представленные диаграммы служат иллюстрацией этапов поразрядной сортировки для файлов с произвольной организацией, файлов с распределением Гаусса, почти отсортированных файлов, почти отсортированных в обратном порядке файлов, файлов с произвольной организацией, обладающих 10 различными ключами (слева направо). Длина каждого файла равна 200. Время выполнения не зависит от исходного порядка входных данных. Три файла, обладающих одним и тем же набором ключей (первый, третий и четвертый файлы представляют собой перестановки целых чисел от 1 до 200) имеют одни и те же рабочие характеристики на завершающих этапах сортировки.

Опять-таки, это описание ситуации не достаточно точно, поскольку точка разделения приходится на центр только в среднем (поскольку число бит в ключе конечно). Тем не менее, для двоичной быстрой сортировки вероятность того, что разделяющая точка находится в окрестности центра, выше, чем для стандартного метода быстрой сортировки, так что старший член выражения, определяющего время выполнения сортировки, тот же, что и для случая, когда разделение идеально. Подробный анализ, доказывающий этот результат, представляет собой классический пример анализа алгоритмов, впервые выполненный Кнутом в 1973 г. (см. раздел ссылок).

Этот результат обобщается путем его применения к поразрядной сортировке MSD. Тем не менее, поскольку основной интерес для нас представляет время выполнения сортировки, а не символы просматриваемых ключей, мы должны проявлять осторожность, поскольку время выполнения поразрядной сортировки пропорционально величине основания системы счисления Л и не имеет ничего общего с ключами.

Лемма 10.3. Поразрядная сортировка MSD с основанием системы счисления R применительно к файлу размера N требует для выполнения по меньшей мере 2N + 2R шагов.

Поразрядная сортировка MSD требует выполнения по меньшей мере одного прохода сортировки методом подсчета индексных ключей, а подсчет индексных ключей предусматривает по меньшей мере два прохода по записям (один для подсчета, другой для распределения), на что затрачивается по меньшей мере 2N шагов, еще два подхода предназначены для просмотра счетчиков (один для их инициализации в О в начале, другой - для проверки, находятся ли подфайлы в конце), на что уходит по меньшей мере еще 2R шагов.

Доказательство наличия этого свойства практически тривиально, в то же время оно ифает весьма важную роль в нашем понимании поразрядной сортировки MSD. В частности, оно говорит нам, что мы не можем утверждать, что время выполнения сортировки будет меньше в силу того, что Л мало, поскольку R может быть намного больше, чем N. Короче говоря, для сортировки файлов небольших размеров следует использовать другие методы. Этот вывод может служить решением проблемы пустых корзин, которую мы обсуждали в конце раздела 10.3. Например, если R равно 256, а N равно 2, то поразрядная сортировка MSD будет в 128 раз медленнее, чем более простой метод, предусматривающий только сравнение элементов. Рекурсивная структура поразрядной сортировки MSD приводит к тому, что соответствующая рекурсивная профамма будет многократно вызывать себя для большого числа файлов небольших размеров. Поэтому в условиях рассматриваемого примера игнорирование проблемы пустых корзин может привести к тому, что вся поразрядная сортировка замедлится в 128 раз по сравнению с тем, какой она может быть. Что касается промежуточных ситуаций (например, предположим, что R равно 256, а N равно 64), то стоимость не будет настолько катастрофичной, тем не менее весьма существенной. Использование сортировки вставками - не слишком удачный выбор, ибо стоимость N/4 сравнений все еще недопустимо высока; не следует игнорировать проблему пустых корзин в силу того факта, что их очень много. Простейший путь решения этой проблемы состоит в использовании основания системы счисления, которая меньше размера сортируемого файла.

Лемма 10.4. Если основание системы счисления всегда меньше размера файла, то в худшем случае число шагов, выполняемых поразрядной сортировкой MSD, учитывается постоянным множителем небольшой величины при IorN (для ключей, содержащих случайные байты) и постоянным множителем небольшой величины при числе байтов в ключе.

Полученный для худшего случая результат вытекает непосредственно из предыдущих рассуждений, и анализ, выполненный для леммы 2, служит обобщением, позволяющим получить оценку для среднего случая. Для большого R множитель logjiN принимает малое значение, так что для практических применений можно считать, что общее время пропорционально N. Например, если Л = 216, то logN меньше 3 для всех N < 2 *, при этом можно с уверенностью утверждать, что это число охватывает все возможные на практике размеры файлов.

Как и в случае леммы 2, на основании леммы 4 мы можем сделать важный для практических приложений вывод о том, что поразрядная сортировка MSD фактически является сублинейной функцией от общего числа разрядов в случайных ключах достаточно большой длины. Например, при сортировке 1 миллиона 64-разрядных случайных ключей потребуется проверка от 20 до 30 старших разрядов ключей, что составляет менее половины всех данных.

Лемма 10.5. Трехпутевая поразрядная быстрая сортировка выполняет в среднем 2N\ogN операций сравнения байтов при сортировке N ключей (произвольной длины).

Возможны два поучительных толкования этого результата. Во-первых, если считать рассматриваемый метод эквивалентным разбиению по старшему разряду, применяемому в рамках быстрой сортировки, то (рекурсивно) используя этот метод применительно к подфайлам, нас не должен удивлять тот факт, что общее число операций примерно такое же, как и в случае нормальной быстрой сортировки, но все это - операции сравнения единичных байтов, а не сравнения ключей в полном объеме. Во вторых, рассматривая этот метод под углом зрения рис. 10.13, мы вправе ожидать, что по лемме 3 время выполнения logyv должно быть помножено на 2 In/?, поскольку требуется 2R\nR шагов быстрой сортировки, чтобы отсортировать R байтов, в отличие от шагов для тех же байтов в случае бинарного дерева. Полное доказательство мы опускаем (см. раздел ссылок).

Лемма 10.6. Поразрядная сортировка LSD может сортировать N записей с w-разрядными ключами за w / \gR проходов, при этом используется дополнительное пространство памяти для R счетчиков (и буфер для переупорядочения файла).

Доказательство этого факта непосредственно вытекает из реализации. В частности, если мы примем R = 2 *, мы получим четырехпроходную линейную сортировку.

Упражнения

10.39. Предположим, что входной файл состоит из 1000 копий каждого числа от 1 до 1000, каждое представлено в виде 32-разрядного слова. Покажите, как вы воспользуетесь этими сведениями, чтобы получить быстрый вариант поразрядной сортировки.