for (i = 1; i <= г; i++)

count[digit(a[i], d) + 1]++;

for (j = 1; j < R;

count[j] += count[j-l];

for (i = 1; i <= r; i++)

aux[count[digit(a[i], d)]++]

for (i = 1; i <= r; i++) a[i]

a[i]; aux[i];

Рисунок 15 иллюстрирует работу двоичной поразрядной сортировки LSD на условном примере упорядочения ключей, благодаря чему становится возможным сравнение с рис. 10.3. Для рассматриваемых 5-разрядных ключей полное упорядочение достигается за пять проходов по ключам справа налево. Сортировка записей с одноразрядным ключом сводится к разбиению файла таким образом, что все записи с ключом О следуют раньше всех записей с ключом 1. Как только что было показано, мы не можем пользоваться стратегией разбиения, которую мы в рассматривали в начале данной главы при обсуждении программы 10.1, несмотря на то, что она по всем признакам решает ту же проблему, в силу того, что она не устойчива. Имеет смысл рассмотреть поразрядную сортировку с основанием системы счисления, равным 2, поскольку во многих случаях ее удобно реализовать на высокопроизводительных машинах и в аппаратном обеспечении специального назначения (см. упражнение 10.38). В программах мы используем максимально возможное число разрядов с тем, чтобы уменьшить число проходов, которое ограничено только размерами массива рассматриваемых чисел (см. рис. 10.16).

А ,0001 S 1-0011

О .01111

R t о о } О-

1 а t 00

й 1 о q 1 0Ч.1 1 о о о .1 t 5 0 0 19 1

f 1.0D.0:

0 0 0 0 1

о 1 1 Э 1

t 0S0-0 0 1100 о D 1 о 1

N G Е X А М Р L Е

R Т N X Р

10 0 1

1 о 1 do

о 1 1 ,1 t 10 10 0 0 0

L 0 110 0 А о о о 01 S 1 о о т О о 1 11

о 1-0 о 0 0 11

0 0 го

on 0 0 0 110 о 0.1 о

G Е А М Е

L А I

М Е R N S О G

1 о 1 1 1 о 1 о о 1 1 00 о 1 о о 1 о о о

о 1 1

0 о 1

1 о ?

0 t 1

1 0 0 о 1 1 ь о 1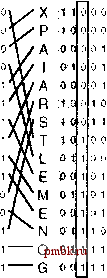

А А R S Т Е Е G X I

N о О о

о I) о о

о о 1

о о о 1

о 1 о

0 1 1

1 d о 1 о 1 1 о 1

1 1 1

о о о

0 о 1

1 о о 1 о 1 1 1 о

-1 1 1

А А Е Е G I

М N О Р R S Т X

о о о 1 о у о 1 0 10 1 о 1 о 1

0 111 10 0 1

1 1 о о

110 1 1110

1111

0 0 0 0 0 0 10 0 0 11

0 10 0

1 о о о

РИСУНОК 10.15. ПОРАЗРЯДНАЯ (ДВОИЧНАЯ) СОРТИРОВКА LSD (ПОКАЗАНЫ РАЗРЯДЫ КЛЮЧЕЙ)

Данная диаграмма служит иллюстрацией использования поразрядной сортировки справа налево, разряд за разрядом, применительно к рассматривавшемуся выше файлу учебному ключей. Мы вычисляем i-u столбец из (/ - 1)-го столбца файла, извлекая (не нарушая при этом свойства устойчивости) все ключи с О в i-м разряде, а затем все ключи с 1 в i-м разряде. Если перед операцией извлечения (/ - \)-й столбец был упорядочен по i - \ замыкающим разрядам ключей, то и i-u столбец будет упорядочен по i замыкающим разрядам ключей по окончании этой операции. Перемещение ключей на третьей стадии пояснений не требует.

Применение подхода LSD к сортировке строковых данных обычно сопряжено с некоторыми трудностями, что в первую очередь объясняется переменной длиной ключей. В случае сортировок MSD достаточно просто отличать один ю1юч от другого по их старшим байтам, однако в основе сортировок лежит принцип постоянной длины ключа, при этом ведущие ключи используются только на заключительных проходах. По всей видимости, даже в случае ключей (большой) фиксированной длины, поразрядная сортировка LSD выполняет бесполезную работу на правой стороне ключей, ибо, как мы смогли убедиться выше, в процессе сортировки обычно используется только левая часть каждого ключа. В разделе 10.6 мы найдем способ решения этой проблемы после того, как подробно изучим свойства поразрядной сортировки.

Упражнения

10.32. Используя генератор ключей из упражнения 10.19 выполнить поразрядную сортировку LSD для N= 10 10\ 10 и 10 Выполнить сравнение показателей этой сортировки с параметрами поразрядной сортировкой MSD.

10.33. Используя генератор ключей из упражнения 10.21 и 10.23 выполнить поразрядную сортировку LSD для Л= 10\ 10*, 10 и 10. Выполнить сравнение показателей этой сортировки с параметрами поразрядной сортировкой MSD.

10.34. Представить (неотсортированный) результат попытки применения поразрядной сортировки, в основу которой положен метод разбиения, используемый в методе двоичной быстрой сортировки, для примера, представленного на рис. 10.15.

010.35. Представить результаты использования поразрядной сортировки LSD для упорядочения по двум первым символам совокупности ключей now is tiie time for all good people to come tiie aid of their party.

10.36. Разработать реализацию поразрядной сортировки LSD, используя связные списки.

10.37. Найти эффективный метод, который (/) переупорядочивает записи файла таким образом, что те их них, ключи которых начинаются с бита О, идут раньше тех записей, ключи которых начинаются с бита 1, ( ) использует дополнительное пространство памяти, пропорциональное квадратному корню из числа записей (или меньше того) и (ш) является устойчивым.

РИСУНОК 10.16. ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОРАЗРЯДНОЙ СОРТИРОВКИ LSD На диаграмме показаны этапы поразрядной сортировки LSD 8-разрядных ключей, принимающих случайные значения, с основанием 2 (слева) и 4, последняя заключает в себе все другие этапы, представленные на диаграмме для основания 2 (справа). Например, когда остаются два разряда (второй этап с конца в левой диаграмме, предпоследний в правой диаграмме) рассматриваемый файл состоит из четырех взаимно проникающих отсортированных подфайлов, состоящих из ключей, начинающихся с 00, 01, 10 и 11.

10.38. Разработать программу, которая сортирует массив 32-разраядных слов, используя всего лишь одну следующую абстрактную операцию: задано положение разряда / и указатель на массив а[к]; упорядочить а[к], а[к+1], а[к+63] посредством устойчивого метода таким образом, что слова с битом О в положении располагаются раньше слов с битом 1 в позиции /.

10.6. Рабочие характеристики поразрядных сортировок

время выполнения поразрядной сортировки LSD при сортировке записей N с ключами, состоящими из w байтов, пропорционально Nw, поскольку соответствующий алгоритм производит w проходов по всем N ключам. Как показывает рис.10.17, это свойство не зависит от природы входных данных.

Для случая длинных ключей и коротких байтов это время сопоставимо с MgTV: например, если мы используем двоичную поразрядную сортировку LSD для сортировки 1 миллиарда 32 разрядных ключей, то как н , так и IgA примерно равны 32. Для более коротких ключей и более длинных байтов время выполнения сортировки сопоставимо с N\ например, если по отношению к 64-разрядным ключам используется 16-разрядное основание системы счисления, то w принимает значение 4, что можно считать константой малого значения.

Чтобы должным образом выполнить сравнение рабочих характеристик поразрядной сортировки с характеристиками алгоритмов, построенных на основе операции сравнения, мы долее подробно должны проанализировать каждый байт ключей, а не ограничиваться только учетом числа ключей.

Лемма 10.1. В худшем случае поразрядная сортировка выполняет проверку всех байтов и всех ключей.

Другими словами, различные виды поразрядной сортировки суть линейные сортировки в том смысле, что затрачиваемое на нее время в большинстве случаев пропорционально количеству цифр во входных данных. Этот факт непосредственно следует из анализа программ: ни одна из цифр не проверяется дважды. Из всех программ, которые мы проверили, худший случай имел место, когда все ключи обладали одними и теми же значениями.

Как мы могли убедиться выше, в случае ключей, принимающих случайные значения, равно как и в во многих других случаях, время выполнения поразрядной сортировки MSD может быть сублинейным по отношению к общему числу битов данных, поскольку не во всех ситуациях можно выполнять полный просмотр конкретного ключа. Для ключей произвольной длины справедливо следующее утверждение:

Лемма 10.2. Двоичная быстрая сортировка в среднем производит проверку N \gN разрядов при сортировке ключей, состоящих их битов, принимающих случайное значение.

Если размер файла выражается степенью 2, а составляющие его биты принимают случайные значения, то естественно предположить, что одна половина старших битов принимает значение О, а другая половина - значение 1, так что рекуррентное соотношение = 2Сщ + описывает возникшую ситуацию, как мы установили при обсуждении свойств быстрой сортировки в главе 7.